大家好，我是人见人爱，花见花开，车见车爆胎的树状数组Peter Pan，hhh

讲正文前，先来一个长文警告⚠很重要的知识点：L SB（SB？）

LSB

怎么算呢？

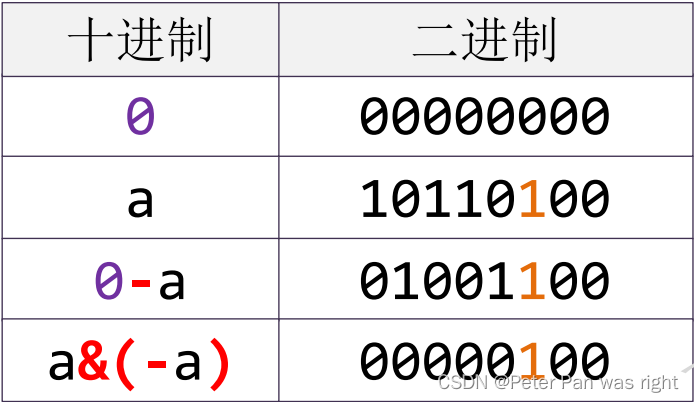
哦……懂了，代码应该长这样

int lowbit(int n){ return n&(-n);}

来，既然懂了，给大家做一道题吧

答案应该是B啊

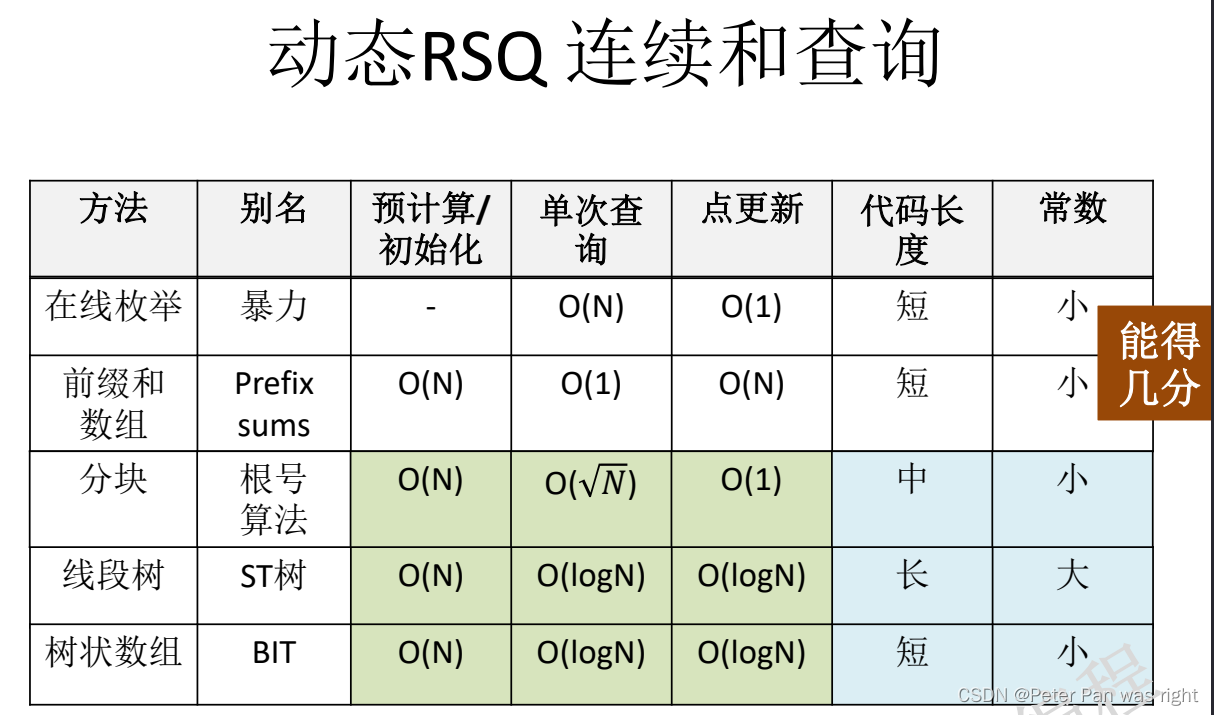
二进制索引树（树状数组）

那么，我们如果用我们学过的算法来做的话，能得几分呢？

基本思想

根据任意正整数关于2的不重复次幂的唯一分解性质，若一个正整数x的二进制表示为10101，其中等于1的位是0，2，4，则正整数x可以被“二进制分解”成。进一步地，区间[1,x]也可以分成个小区间：

①长度为的小区间[1,]

②长度为的小区间[,]

③长度为的小区间[,]。树状数组就是以上的思想。

我们建立一个数组c，其中c[x]保存序列A的区间[x-lowbit(x)+1,x]中所有数之和。其实，c数组可以被化成一个树

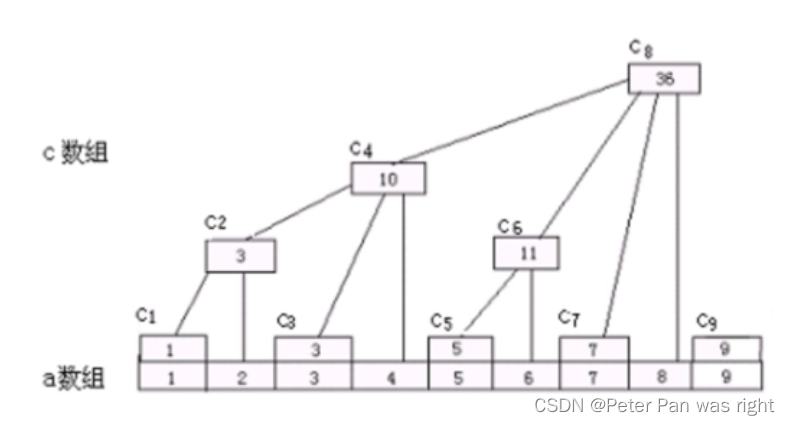
这个树的重要性质是“除树根外，每个内部节点c[x]的父节点是c[x+lowbit(x)]”。

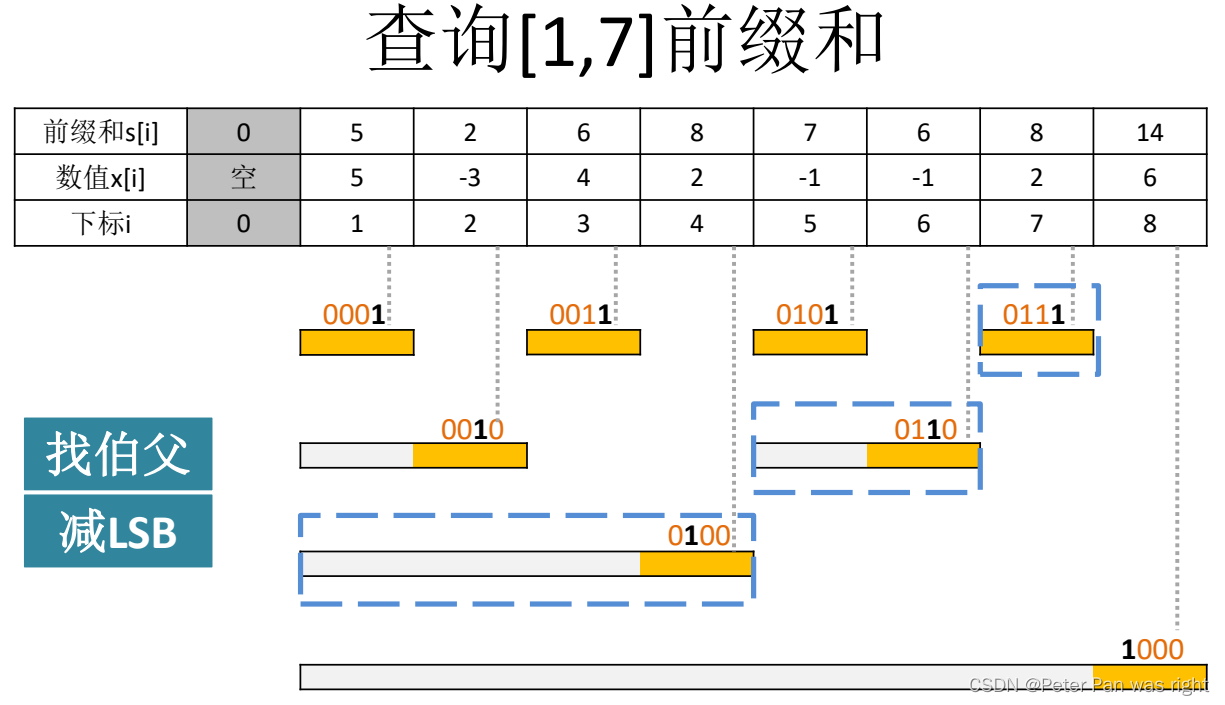
那么，我怕你们还是不懂，请看下图

先给大家看看查询前缀和的代码吧

int sum(int i){int ans=0;while(i){ans+=c[i];i-=lowbit(i);}return ans;
}

有人会问了，为什么i要自减lowbit(i)呢？因为上一步的c[i]表示[i-lowbit(i)+1,i]，为了连续，下一步结尾要是i-lowbit(i)，所以说我们要用i-=lowbit(i)衔接。

大家查询懂了，那么更新怎么实现呢？给数组内A[x]加上一个y，主要影响的是上上上图中c[x]的所有祖先，由上上上图的性质知c[x]的父节点是c[x+lowbit(x)]，也就是说，我们要不断地加lowbit(x)，下面给出代码

void update(int x,int y){while(x<=n){c[x]+=y;x+=lowbit(x);}
}

那么，核心代码讲完了，怎么，看我干嘛，做题啊啊啊啊

最强大脑之八

题目描述

lester参加最强大脑比赛，比赛内容是默记对一个序列的操作 序列长度固定为n，初始取值均为0 每次操作由3个数描述：t,x,y，其中 t=1：表示要求写下序列第x到y个位置上（包含x,y）的数值之和，取模100000007的余数 t=2：表示序列的第x个位置上的数加上y lester靠心算就能完成这些简单的操作，你就不行了，所以你只能写代码实现（怎么，贬低我？）