文章目录
- 概述
- 1 连续数值变量
- 1.1 ParCorr 偏相关(ParCorr类)
- 1.2 鲁棒偏相关(RobustParCorr)
- 非线性检验
- 1.3 GPDC
- 1.4 CMIknn
- 2a. 分类/符号时间序列
- 2b. 混合分类/连续时间序列
- 多变量X和Y的测试
概述
这个表格概述了 X ⊥ Y ∣ Z X\perp Y | Z X⊥Y∣Z的测试及其相关的假设
| 条件独立性检验 | 假设条件 |
|---|---|
| ParCorr | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系和高斯噪声; X , Y X,Y X,Y必须是单变量 |
| RobustParCorr | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系,对不同边缘分布具有鲁棒性; X , Y X,Y X,Y必须是单变量 |
| ParCorrWLS | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系,可以处理异方差依赖关系; X , Y X,Y X,Y必须是单变量 |
| GPDC / GPDCtorch | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有加性依赖关系; X , Y X,Y X,Y必须是单变量 |
| CMIknn | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有更一般的依赖关系(基于排列的检验); X , Y X,Y X,Y可以是多变量 |
| Gsquared | 离散/分类变量 X , Y , Z X,Y,Z X,Y,Z; X , Y X,Y X,Y必须是单变量 |
| CMIsymb | 离散/分类变量 X , Y , Z X,Y,Z X,Y,Z(基于排列的检验); X , Y X,Y X,Y 可以是多变量 |
| RegressionCI | 混合数据集,包含单变量离散/分类和(线性)连续变量 X , Y , Z X,Y,Z X,Y,Z; X , Y X,Y X,Y必须是单变量 |
| PairwiseMultCI | 元条件独立性检验,将上述每个单变量检验转变为多变量检验,包括可能有助于增加效应大小的方法 |
在概述教程中讨论的密度图可以帮助选择使用哪种测试。
需要注意的是,那些假设条件较少的测试通常比假设条件较多的测试具有更低的检测能力。例如,对于实际上是线性的依赖关系,ParCorr的效果会比CMIknn好得多。此外,非参数测试在计算上要昂贵得多。
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearnimport tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toysfrom tigramite import plotting as tp
from tigramite.pcmci import PCMCIfrom tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.parcorr_wls import ParCorrWLS
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.independence_tests.gsquared import Gsquared
from tigramite.independence_tests.regressionCI import RegressionCI
1 连续数值变量
1.1 ParCorr 偏相关(ParCorr类)
在概述教程中有解释。
1.2 鲁棒偏相关(RobustParCorr)
如果在数据中仍然存在线性依赖关系,但分布又不是高斯分布,建议使用鲁棒偏相关(RobustParCorr)测试。这种测试在进行偏相关测试之前,会先将数据转换为正态分布1。
在这里,我们还展示了新的函数toys.generate_structural_causal_process,它允许随机创建具有一定数量参数的结构因果过程模型(详见文档说明)。在接下来的示例中,噪声项来自于极值Weibull分布和均匀分布。此外,我们还应用了一些多项式变换,使数据变得更加极端。
# np.random.seed(1)
T = 500
links, noises = toys.generate_structural_causal_process(N=3, L=4, dependency_funcs=['linear'], dependency_coeffs=[-0.5, 0.5], auto_coeffs=[0.3, 0.5], contemp_fraction=0.,max_lag=2, noise_dists=['weibull', 'uniform'],noise_means=[0.],noise_sigmas=[1., 1.5],noise_seed=5,seed=9)
for j in links:print(j, [(link[0], link[1], link[2].__name__) for link in links[j]])print(noises[j].__name__)
data, nonstat = toys.structural_causal_process(links,T=T, noises=noises)
data[:,0] = data[:,0] + 0.3*data[:,0]**3
data[:,1] = data[:,1] + 0.3*data[:,1]**5
data[:,2] = np.sign(data[:,2])*data[:,2]**2
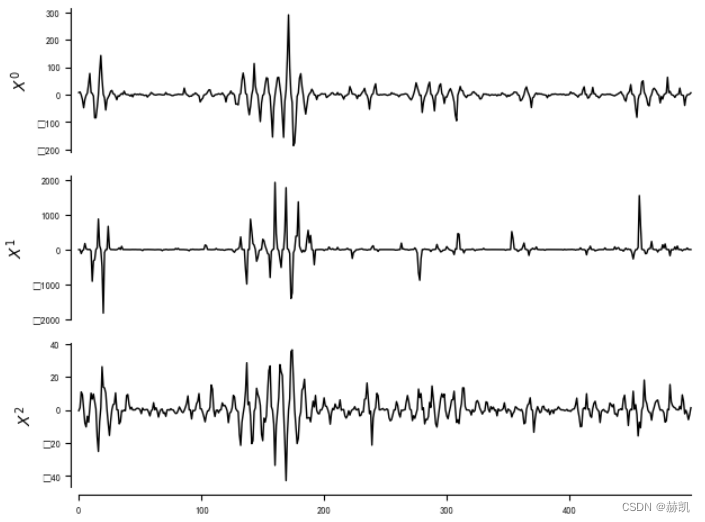
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe)
0 [((0, -1), 0.5, ‘linear’), ((2, -1), -0.5, ‘linear’), ((1, -2), 0.5, ‘linear’)]
weibull
1 [((1, -1), 0.3, ‘linear’), ((0, -2), -0.5, ‘linear’)]
weibull
2 [((2, -1), 0.3, ‘linear’), ((0, -2), 0.5, ‘linear’)]
uniform
# Init
pcmci_robust_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=RobustParCorr())
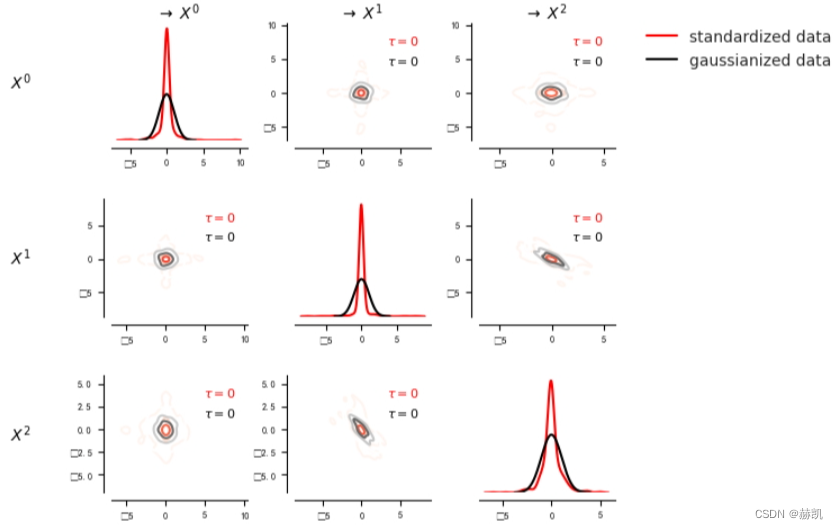
我们可以使用密度图功能来展示偏斜的边缘和联合密度。在这里,我们将偏斜的数据标准化,以显示它明显非高斯分布。
# tp.plot_densityplots(dataframe=dataframe, add_densityplot_args={'matrix_lags':matrix_lags}); plt.show()
# correlations = pcmci_robust_parcorr.get_lagged_dependencies(tau_max=20, val_only=True)['val_matrix']
# matrix_lags = np.argmax(np.abs(correlations), axis=2)
matrix_lags = Nonematrix = tp.setup_density_matrix(N=dataframe.N, var_names=dataframe.var_names)# Standardize to better compare skewness with gaussianized data
dataframe.values[0] -= dataframe.values[0].mean(axis=0)
dataframe.values[0] /= dataframe.values[0].std(axis=0)matrix.add_densityplot(dataframe=dataframe, matrix_lags=matrix_lags, label_color='red', label="standardized data",snskdeplot_args = {'cmap':'Reds', 'alpha':1., 'levels':4})# Transform data to normal marginals
data_normal = pp.trafo2normal(data)
dataframe_normal = pp.DataFrame(data_normal, var_names=var_names)matrix.add_densityplot(dataframe=dataframe_normal, matrix_lags=matrix_lags, label_color='black', label="gaussianized data",snskdeplot_args = {'cmap':'Greys', 'alpha':1., 'levels':4})
matrix.adjustfig()
# plt.show()
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr())
results = pcmci_parcorr.run_pcmci(tau_max=2)pcmci_robust_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=RobustParCorr())
results_robust = pcmci_robust_parcorr.run_pcmci(tau_max=2)fig, axes = plt.subplots(nrows=1, ncols=3)
axes[0].set_title("True graph")
tp.plot_graph(graph=pcmci_robust_parcorr.get_graph_from_dict(links, tau_max=None),var_names=var_names,fig_ax=(fig, axes[0]),show_colorbar=False,)axes[1].set_title("ParCorr")
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,fig_ax=(fig, axes[1]),show_colorbar=False,)axes[2].set_title("RobustParCorr")
tp.plot_graph(val_matrix=results_robust['val_matrix'],graph=results_robust['graph'],var_names=var_names,fig_ax=(fig, axes[2]),show_colorbar=False,)
plt.show()
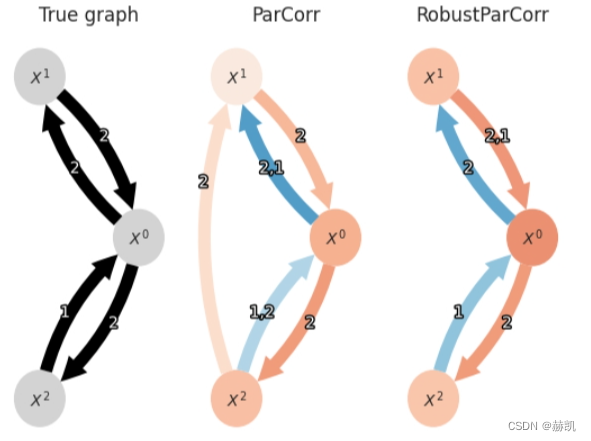
鲁棒偏相关(右图)在这里比标准的偏相关(左图)产生更可靠的结果,因为边缘分布事先被转换为正态分布。
在教程tigarite_tutorial_heteroskedastic_ParCorrWLS中,我们介绍了另一种适用于异方差数据的偏相关版本,称为ParCorrWLS。
非线性检验
如果存在非线性依赖关系,建议使用非参数检验。
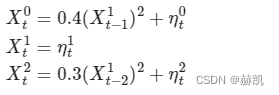
random_state = np.random.default_rng(seed=42)
data = random_state.standard_normal((500, 3))
for t in range(1, 500):data[t, 0] += 0.4*data[t-1, 1]**2data[t, 2] += 0.3*data[t-2, 1]**2
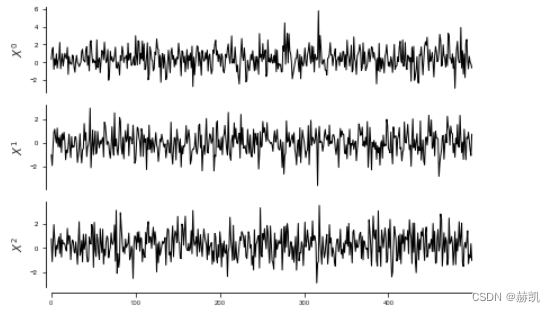
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr(),verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
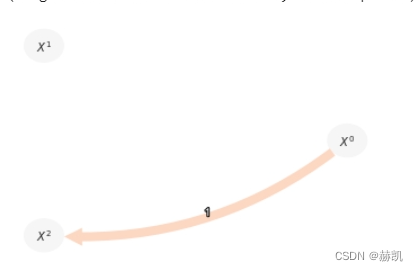
偏相关在这里有两个失败之处:(1)它无法检测到两个非线性链接;(2)它错误地检测到了一个链接,因为它同样无法排除非线性依赖。
1.3 GPDC
Tigramite通过基于高斯过程回归和残差上的距离相关性(GPDC)的测试来覆盖非线性加性依赖关系。对于GPDC,没有可用的距离相关性(DC)的解析空模型分布。为了进行显著性检验,Tigramite通过参数significance = 'analytic'预先计算每个样本大小的分布(存储在内存中),从而避免了对每个条件独立性测试进行计算成本高昂的排列测试(significance = 'shuffle_test')。高斯过程回归使用sklearn的默认参数执行,除了核函数在这里默认为径向基函数+一个白噪声核(这两个超参数在内部被优化),以及假定的噪声水平alpha被设置为零,因为我们添加了一个白噪声核。这些和其他参数可以通过gp_params字典来设置。有关进一步讨论,请参见sklearn的文档。还存在一个模块(gpdc_torch.py),它利用gpytorch在GPU上进行更快的计算。
gpdc = GPDC(significance='analytic', gp_params=None)
pcmci_gpdc = PCMCI(dataframe=dataframe, cond_ind_test=gpdc,verbosity=0)
与偏相关(ParCorr)相比,非线性链接被GPDC正确检测到。
results = pcmci_gpdc.run_pcmci(tau_max=2, pc_alpha=0.1, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
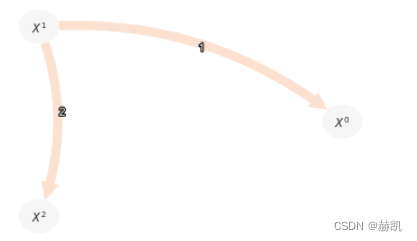
作为一个简短的离题,我们可以通过观察散点图来了解GPDC是如何工作的。
array, dymmy, dummy, dummy = gpdc._get_array(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)
x, meanx = gpdc._get_single_residuals(array, target_var=0, return_means=True)
y, meany = gpdc._get_single_residuals(array, target_var=1, return_means=True)fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(8,3))
axes[0].scatter(array[2], array[0], color='grey', alpha=0.3)
axes[0].scatter(array[2], meanx, color='black')
axes[0].set_title("GP of %s on %s" % (var_names[0], var_names[1]) )
axes[0].set_xlabel(var_names[1]); axes[0].set_ylabel(var_names[0])
axes[1].scatter(array[2], array[1], color='grey', alpha=0.3)
axes[1].scatter(array[2], meany, color='black')
axes[1].set_title("GP of %s on %s" % (var_names[2], var_names[1]) )
axes[1].set_xlabel(var_names[1]); axes[1].set_ylabel(var_names[2])
axes[2].scatter(x, y, color='red', alpha=0.3)
axes[2].set_title("DC of residuals:" "\n val=%.3f / p-val=%.3f" % (gpdc.run_test(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)) )
axes[2].set_xlabel("resid. "+var_names[0]); axes[2].set_ylabel("resid. "+var_names[2])
plt.tight_layout()
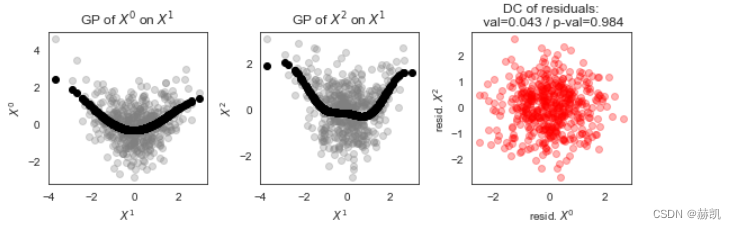
让我们来看一个具有乘性噪声的模型中更为非线性的依赖关系:
random_state = np.random.default_rng(seed=11)
data = random_state.standard_normal((600, 3))
for t in range(1, 600):data[t, 0] *= 0.2*data[t-1, 1]data[t, 2] *= 0.3*data[t-2, 1]
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()

由于乘性噪声违反了GPDC所基于的加性依赖的假设,虚假的链接被错误地检测出来,因为它无法被排除条件。然而,与ParCorr相比,两个真实的链接被检测出来,因为距离相关性(DC)可以检测到任何类型的依赖关系(底层的sklearn高斯过程函数可能会发出警告):
pcmci_gpdc = PCMCI(dataframe=dataframe, cond_ind_test=gpdc)
results = pcmci_gpdc.run_pcmci(tau_max=2, pc_alpha=0.1, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
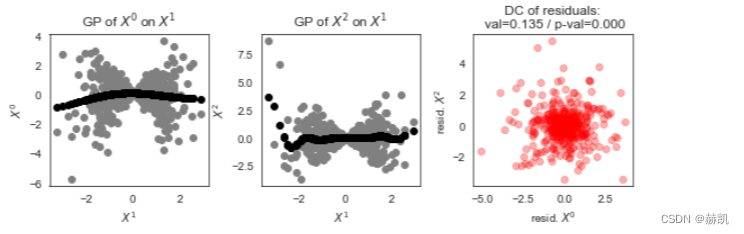
在这里的散点图中,我们可以看到高斯过程无法很好地拟合依赖关系,因此残差不是独立的。
array, dymmy, dummy, dummy = gpdc._get_array(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)
x, meanx = gpdc._get_single_residuals(array, target_var=0, return_means=True)
y, meany = gpdc._get_single_residuals(array, target_var=1, return_means=True)fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(8,3))
axes[0].scatter(array[2], array[0], color='grey')
axes[0].scatter(array[2], meanx, color='black')
axes[0].set_title("GP of %s on %s" % (var_names[0], var_names[1]) )
axes[0].set_xlabel(var_names[1]); axes[0].set_ylabel(var_names[0])
axes[1].scatter(array[2], array[1], color='grey')
axes[1].scatter(array[2], meany, color='black')
axes[1].set_title("GP of %s on %s" % (var_names[2], var_names[1]) )
axes[1].set_xlabel(var_names[1]); axes[1].set_ylabel(var_names[2])
axes[2].scatter(x, y, color='red', alpha=0.3)
axes[2].set_title("DC of residuals:" "\n val=%.3f / p-val=%.3f" % (gpdc.run_test(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)) )
axes[2].set_xlabel("resid. "+var_names[0]); axes[2].set_ylabel("resid. "+var_names[2])
plt.tight_layout()
1.4 CMIknn
Tigramite中实现的最通用的条件独立性测试是基于使用k-最近邻估计器估计的条件互信息(CMIknn)。这个测试在下面的论文中有描述:
Runge, Jakob. 2018. “基于条件互信息最近邻估计器的条件独立性测试。” 载于第21届国际人工智能与统计会议论文集。
CMIknn不涉及对依赖关系的明确假设。然而,由于密度是通过局部样本超点隐式近似的,因此有一个假设是这些超立方体内密度是恒定的。参数knn决定了超立方体的大小,即(数据自适应的)局部长度尺度。
现在我们甚至不能预计算空模型分布,因为CMIknn不像GPDC那样基于残差,空模型分布依赖于更多因素。因此,我们使用significance='shuffle_test'在每个单独的测试中生成它。测试的洗牌测试 I ( X ; Y ∣ Z ) = 0 I(X;Y|Z)=0 I(X;Y∣Z)=0随机 X X X值是局部的:每个样本点 x x x的值被随机映射到其最近邻居中的一个(shuffle_neighbors参数)在子空间 Z Z Z中。另一个可选参数是transform,它指定在CMI估计之前是否转换数据。新的默认值是transform=ranks,它比旧的transform=standardize效果更好。下面的单元可能需要几分钟时间。
# cmi_knn = CMIknn(significance='shuffle_test', knn=0.1, shuffle_neighbors=5, transform='ranks', sig_samples=200)
# pcmci_cmi_knn = PCMCI(
# dataframe=dataframe,
# cond_ind_test=cmi_knn,
# verbosity=0)
# results = pcmci_cmi_knn.run_pcmci(tau_max=2, pc_alpha=0.05, alpha_level = 0.01)
# tp.plot_graph(
# val_matrix=results['val_matrix'],
# graph=results['graph'],
# var_names=var_names,
# link_colorbar_label='cross-MCI',
# node_colorbar_label='auto-MCI',
# vmin_edges=0.,
# vmax_edges = 0.3,
# edge_ticks=0.05,
# cmap_edges='OrRd',
# vmin_nodes=0,
# vmax_nodes=.5,
# node_ticks=.1,
# cmap_nodes='OrRd',
# ); plt.show()
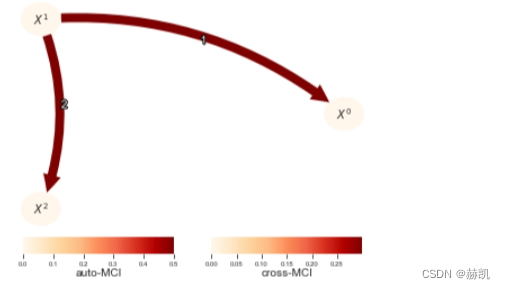
在这里,CMIknn正确地检测到了真实的链接,并且也揭示了虚假的链接。虽然CMIknn现在可能看起来是最好的独立性测试选择,我们必须注意到,这种通用性是以更低的检测能力为代价的,即当依赖关系实际上遵循某种参数形式时。那么,ParCorr或GPDC是更有力的措施。当然,ParCorr也比GPDC更好地检测线性链接。
另外需要注意的是:由于洗牌测试,CMIknn的计算成本非常高。你可以通过sig_samples参数减少洗牌样本的数量(以增加p值估计的误差为代价)。
或者,你可以使用significance='fixed_thres'选项。然后,pc_alpha被解释为任何条件独立性测试中的(单边)阈值 I ∗ I^* I∗。然后不会进行条件独立性假设检验。对于测试统计量 I ( X ; Y ∣ Z ) I(X;Y|Z) I(X;Y∣Z)
的条件独立性的标准则是
I ( X ; Y ∣ Z ) < I ∗ I(X;Y|Z)<I^* I(X;Y∣Z)<I∗
I ∗ I^* I∗应被视为超参数。请注意,为CMIknn选择 I ∗ I^* I∗是棘手的,因为 I ( X ; Y ∣ Z ) I(X;Y|Z) I(X;Y∣Z)的值取决于变量的维度,由于有限样本的估计偏差。好的一面是,即使这样,CMIknn也相当快。
然后,你也可以使用像pc_alpha = [0.001, 0.005, 0.01, 0.05](或任何其他你选择的阈值列表)。然后计算所有这些阈值的图形,并使用CMIknn的(新)get_model_selection_criterion函数在这些图形中选择。该函数使用sklearn的cross_val_score(基于模型选择_folds的k折交叉验证集)和KNeighborsRegressor模型(与估计器的邻居数量相同,但使用标准的欧几里得范数)在每个节点上使用其在给定阈值产生的图形中的父节点。它将返回最小分数(预测误差)的结果。
这个选项只对依赖于排列测试的条件独立性测试有意义,这些测试是CMIknn和CMIsymb.
# Pick pc_alpha here interpreted as fixed threshold with significance='fixed_thres'
pc_alpha = 0.05 #[0.001, 0.005, 0.01, 0.025, 0.05, 0.1]cmi_knn = CMIknn(significance='fixed_thres', model_selection_folds=3)
pcmci_cmi_knn = PCMCI(dataframe=dataframe, cond_ind_test=cmi_knn, verbosity=0)
results = pcmci_cmi_knn.run_pcmciplus(tau_max=2, pc_alpha=pc_alpha)
# if fixed_thres is used, pc_alpha (and alpha_level) is interpreted as a threshold on the test statistic.tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.3,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
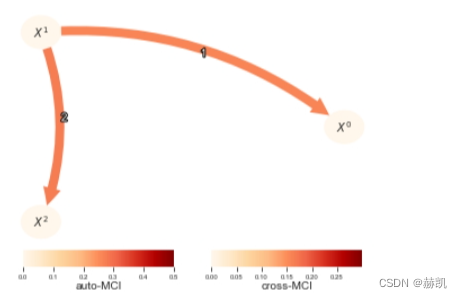
在这个例子中,选择 pc_alpha = [0.001, 0.005, 0.01, 0.025, 0.05, 0.1] 并不能得到正确的结果。阈值设定没有统计检验的严谨性,但可以帮助进行因果特征选择或在更大的机器学习流水线中使用因果发现等任务。
2a. 分类/符号时间序列
分类或符号(或离散)数据在值之间没有顺序或度量,比如苹果和梨子。为了适应这类时间序列,Tigramite包括了Gsquared和CMIsymb条件独立性测试。这两种测试都是直接从离散值的直方图估计得出的。为了获得空模型分布,Gsquared使用 x 2 x^2 x2分布(对于零条目调整自由度),这只在渐近情况下有效(取决于数据)。对于较小的样本量,使用CMIsymb类,它包括基于条件互信息的局部排列测试,CMIsymb的计算时间要比Gsquared长得多。
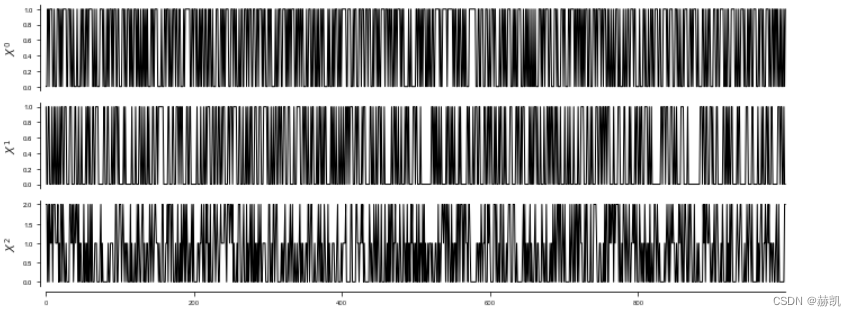
在下面的过程中, X 0 X^0 X0, X 1 X^1 X1有两个类别,而 X 2 X^2 X2有三个。 X 0 X^0 X0, X 2 X^2 X2的概率取决于 X 1 X^1 X1的概率,其中 X 1 X^1 X1充当混杂因子。
T = 1000
def get_data(T, seed=1):random_state = np.random.default_rng(seed)data = random_state.binomial(n=1, p=0.4, size=(T, 3))for t in range(T):prob = 0.4+data[t-1, 1].squeeze()*0.2data[t, 0] = random_state.choice([0, 1], p=[prob, 1.-prob])prob = 0.4+data[t-2, 1].squeeze()*0.2data[t, 2] = random_state.choice([0, 1, 2], p=[prob, (1.-prob)/2., (1.-prob)/2.])return data
dataframe = pp.DataFrame(get_data(T), var_names=var_names)
tp.plot_timeseries(dataframe, figsize=(10,4)); plt.show()
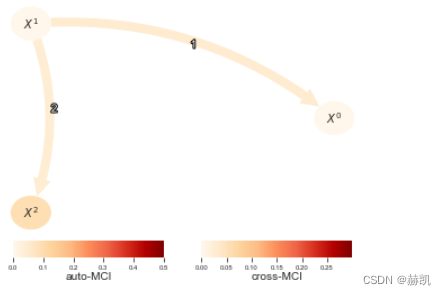
在这里,我们关注Gsquared。请注意,G2统计量值随样本量的大小而变化,但它与条件互信息相关,相关公式为 G = 2 n C M I G = 2nCMI G=2nCMI。其中, n n n是样本量。因此,我们在这里转换val_matrix以获得更好解释(和可绘图的)量。
gsquared = Gsquared(significance='analytic')
pcmci_cmi_symb = PCMCI(dataframe=dataframe, cond_ind_test=gsquared)
results = pcmci_cmi_symb.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)val_matrix = results['val_matrix']
val_matrix /= (2.*T)
tp.plot_graph(val_matrix=val_matrix,graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.3,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
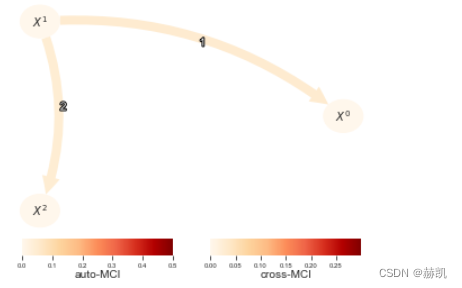
请参考关于CMIsymb的独立教程,以及CMIknnMixed,该教程讨论了如何处理(连续和分类变量的)组合,甚至是同时包含两种类型的变量。
在这里,CMIsymb需要更长的时间并且给出了相同的结果,但对于较小的样本量和更高维度的条件集(和/或更多的分类值),Gsquared的渐近空模型分布可能不再有效,这时更倾向于使用CMIsymb。
# cmi_symb = CMIsymb(significance='shuffle_test')
# pcmci_cmi_symb = PCMCI(
# dataframe=dataframe,
# cond_ind_test=cmi_symb)
# results = pcmci_cmi_symb.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
# tp.plot_graph(
# val_matrix=val_matrix,
# graph=results['graph'],
# var_names=var_names,
# link_colorbar_label='cross-MCI',
# node_colorbar_label='auto-MCI',
# vmin_edges=0.,
# vmax_edges = 0.3,
# edge_ticks=0.05,
# cmap_edges='OrRd',
# vmin_nodes=0,
# vmax_nodes=.5,
# node_ticks=.1,
# cmap_nodes='OrRd',
# ); plt.show()
2b. 混合分类/连续时间序列
通常,人们可能会遇到一种情况,即在数据集中,一些变量是分类的,而另一些是连续的。这种情况可以通过RegressionCI独立性测试来解决。然后,必须通过dataframe的data_type参数为每个变量设置类型。这里更一般地将其实现为与数据形状相同的二进制数据数组,描述变量中的个别样本(或所有样本)是连续的还是离散的:连续变量用0表示,离散变量用1表示。在这里,一个变量的所有样本必须是相同的类型。
# Generate some mixed-type data with a binary variable (can also be multinomial) causing two continuous ones.
random_state = np.random.default_rng(42)
T = 1000
data = np.zeros((T, 3))
data[:, 1] = random_state.binomial(n=1, p=0.5, size=T)
for t in range(2, T):data[t, 0] = 0.5 * data[t-1, 0] + random_state.normal(0.2 + data[t-1, 1] * 0.6, 1)data[t, 2] = 0.4 * data[t-1, 2] + random_state.normal(0.2 + data[t-2, 1] * 0.6, 1)data_type = np.zeros(data.shape, dtype='int')
# X0 is continuous, encoded as 0 in data_type
data_type[:,0] = 0
# X1 is discrete, encoded as 1 in data_type
data_type[:,1] = 1
# X2 is continuous, encoded as 0 in data_type
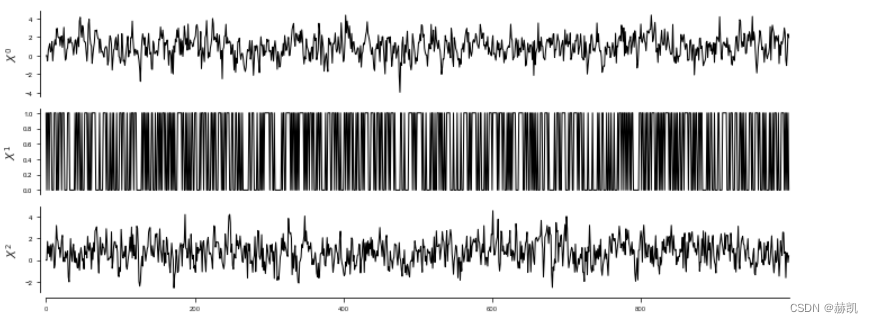
data_type[:,2] = 0dataframe = pp.DataFrame(data,data_type=data_type,var_names=var_names)
tp.plot_timeseries(dataframe, figsize=(10,4)); plt.show()
regressionCI = RegressionCI(significance='analytic')pcmci = PCMCI(dataframe=dataframe, cond_ind_test=regressionCI)
results = pcmci.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Also here the test statistic values are not very useful
val_matrix = results['val_matrix']
val_matrix /= (2.*T)
tp.plot_graph(val_matrix=val_matrix,graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.1,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
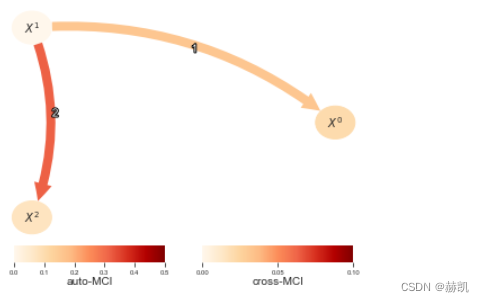
多变量X和Y的测试
上述测试中的几个也适用于多变量X和Y(所有测试都适用于多变量Z)。此外,元类PairwiseMultCI允许将每个单变量测试转换为多变量测试。该类还允许增加条件集,这可以帮助增加效应大小。
查看相应的教程和论文:
Tom Hochsprung, Jonas Wahl*, Andreas Gerhardus*, Urmi Ninad*, 和 Jakob Runge. 增加随机向量间成对条件独立测试的效应大小。UAI2023, 2023。
)
续20个)

)
)

)







![每日一题 --- 前 K 个高频元素[力扣][Go]](http://pic.xiahunao.cn/每日一题 --- 前 K 个高频元素[力扣][Go])


![Useros.environ[“CUDA_VISIBLE_DEVICES“] = “1“](http://pic.xiahunao.cn/Useros.environ[“CUDA_VISIBLE_DEVICES“] = “1“)

