因为文字太过晦涩难懂，下面以图示的方法来理解RSA加密解密的过程

 

 

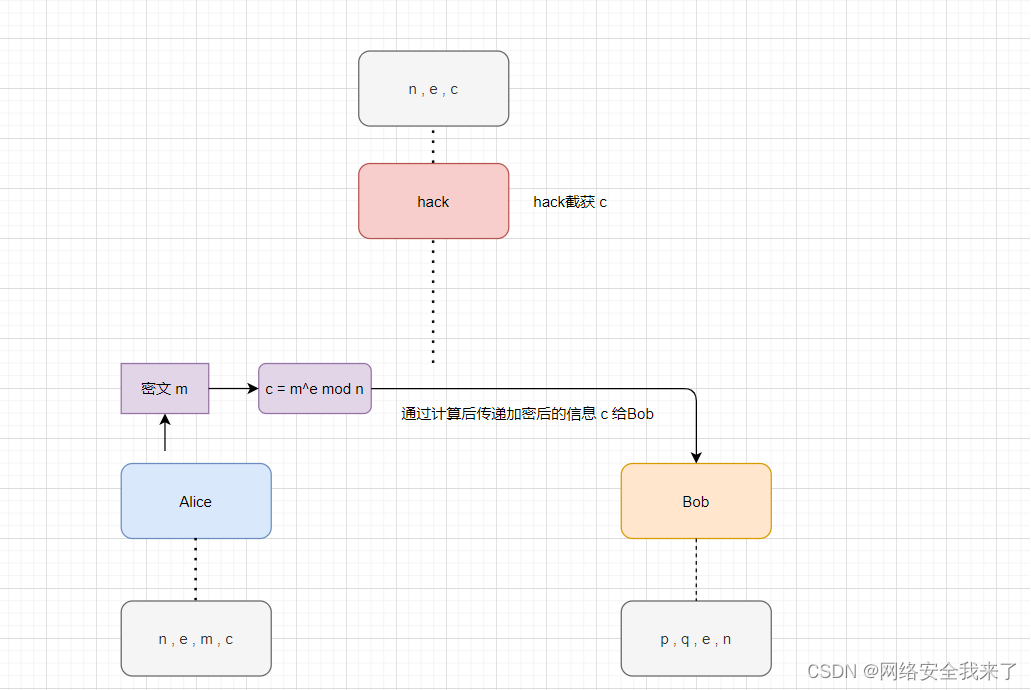
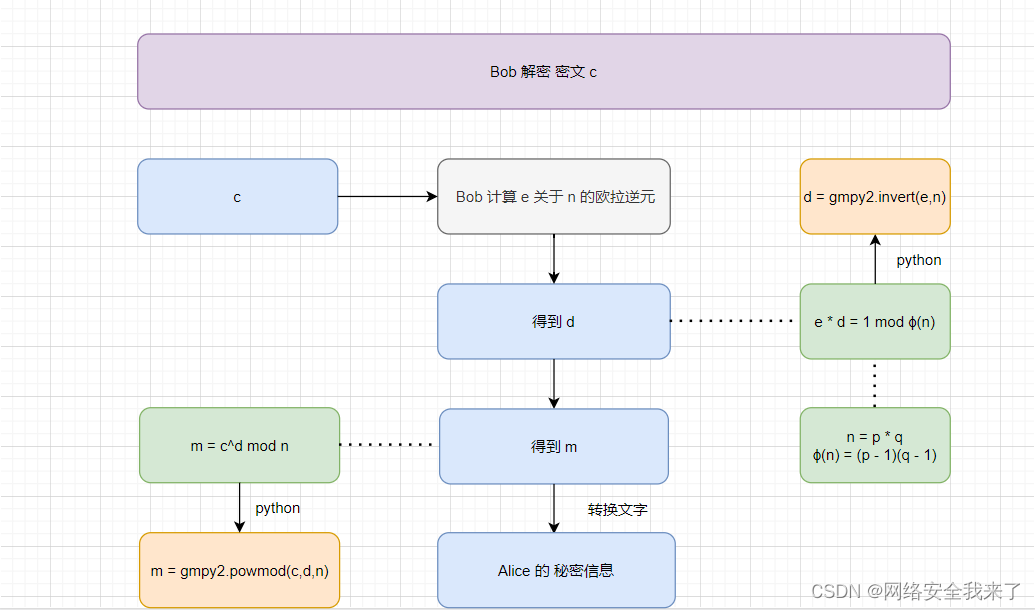
以上过程中因为HACK无法得到p,q信息，也就是无法计算出d , 导致了无法解密 c 得到 m

(n,e) 公钥

(d,n) 私钥

(p,q,n,e) 生成的加密必要信息

必要的公式

c ≡ me mod n -----------> (信息加密) m ≡ cd mod n -----------> (信息解密) ϕ(n) = (p−1)∗(q−1) ----------> (n的欧拉函数) d∗e ≡ 1 mod ϕ(n) ----------> (计算e关于ϕ(n)的逆元)

A 要 向 B 传递信息 m

首先 B  要把  公钥 （n, e）传递给  A

然后  A 拿着公钥  进行 公钥加密算法  将 明文 m  变成 密文 c

接着  A 把 生成的 密文 c  传递 给 B

最后  B 再利用 私钥 （n，d）进行 私钥解密算法 还原出来  明文 m

rsa加密的过程

随便找出两个 整数 q 和 p （q，p互素，即：公因数只有1）

求出n = q * p  

φ(n)= （p-1）*（q-1） 欧拉公式

公钥 e ：   随机取，要求 ：e 和 φ(n) 互素（公因数只有 1）；   1<  e < φ(n)）；

私钥 d ：  ed  ≡  1 （mod  φ(n) ）   （ed 除以 φ(n) 的 余数 为  1 ）

N：大整数N，我们称之为模数（modulus）

p 和 q ：大整数N的两个因子（factor）

e 和 d：互为模反数的两个指数（exponent）

c 和 m：分别是密文和明文

而{N,e}称为公钥,{N,d}称为私钥。总的来说,明文m(一般为flag)就像是一个锁,而私钥{N,d}就是打开这个锁的钥匙。我们要做的就是根据公钥{N,e}来生成这把钥匙来打开锁。而私钥{N,d}中的N又是可以从公钥{N,e}中获得的，所以关键就是在d的获取，d的值和p,q,e有关。p,q又是N的两个因子，所以RSA题目关键便是对N的分解，分解出N的两个因子题目便解决了。这便是RSA题目的思路。

1 已知 p ，q，e   求 d？

p= 18255878996579787209

q= 324206965464727676218470615969477348407

e= 13

import gmpy2p= 18255878996579787209q= 324206965464727676218470615969477348407e= 13phi_n= (p - 1) * (q - 1)d = gmpy2.invert(e, phi_n)print("d is:")print (d)

将获取的d，进行md5加密：d3ba43fb7bbe17d17aa7054a7ed3ac23，得到的结果即为flag。

2 已知 公钥（n, e） 和 密文 c  求 明文 m？

方法一：（n,e不太大的情况下）

首先将  n 用 yafu分解为 q 和 p

再利用脚本 ：

import libnumfrom Crypto.Util.number import long_to_bytesc = 0x6cd55a2bbb49dfd2831e34b76cb5bdfad34418a4be96180b618581e9b6319f86n = 108539847268573990275234024354672437246525085076605516960320005722741589898641#n = int("",16)e = 65537#e = int("",16)q = 333360321402603178263879595968004169219p = 325593180411801742356727264127253758939d = libnum.invmod(e, (p - 1) * (q - 1))m = pow(c, d, n)   # m 的十进制形式string = long_to_bytes(m)  # m明文print(string)  # 结果为 b‘ m ’ 的形式

方法二：（n , e 比较大的时候）

在一个题目中，你拿到了两个n，e都为65537，两个n分别为：

n1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327

n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743

通过直接分解，上factordb都分解失败。通过尝试发现：

print gcd(n1,n2)

打印出：

1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109

则此致即为两个n共有的素因子p，然后进一步求出q，求解完毕。

def gcd(a, b):if a < b:a, b = b, awhile b != 0:temp = a % ba = bb = tempreturn an1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743print gcd(n1,n2)p=1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109q=n1/pprint(q)