目录
1问题: 输入任意进制的数值,可以转换成任意进制的数值(2到36进制);
2思路:
3代码:(需要运用到数据结构栈的知识)
4运行结果:
1问题: 输入任意进制的数值,可以转换成任意进制的数值(2到36进制);
2思路:
因为十进制是中间值,就是任何进制转换成十进制只需要每位乘上自己进制的加权数即可,十进制转换成任意进制可以的逆余数即可

一、十进制转任意进制:
十进制转任意进制时,将这个十进制数除以进制数,比如2(也就是十进制转二进制),得到商和一个从0~1的余数,然后再以这个商为被除数,除了进制数2,继续得到商和一个从0~1的余数。以此方式不断相除,直到得到的商为0为止。此时,得到若干个余数,把这些余数按从后到先的顺序排列起来,那么这个排列起来的值即为该十进制转换成二进制的值。计算如图所示:
最后得到的余数为二进制的非零的最高位,最先得到的余数为二进制的最低位,可知:十进制数9转换成二进制数为1001。
二、任意进制转十进制:
任意进制转十进制时,以二进制数1001为例:该进制的最低位(右一)的值1就表示实际的十进制值1,次低位(右二)的值0表示进制数2的一次方的0倍即为0,次次低位(右三)的值0表示进制数2的二次方4的0倍即为0,最高位(左一)的值1表示进制数2的三次方8的1倍即为8,以此类推,将每位得到的十进制数相加得到9,该和即为二进制数1001对应的十进制数。计算如图所示:
3代码:(需要运用到数据结构栈的知识)
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<iostream>
using namespace std;
#define MAXSIZE 100
#define ok 1
#define error 0
#define ovrflow -1
typedef int status;
typedef struct{int *base;int *top;int stacksize;
}sqstack;
status initlist(sqstack &s);
void input(int x,int &e);
void conversion(sqstack &s,int y,int e);
void push(sqstack &s,int e);//改进
int stackempty(sqstack s);
int pop(sqstack &s,int &e);
int main(){sqstack s;int x,y,m,e=0;while(1){cout<<"请决定将几进制转换为几进制:";cin>>x>>y;cout<<endl<<"请输入具体数值:";input(x,e);if(initlist(s)) cout<<"初始化成功"<<endl;else cout<<"初始化失败";conversion(s,y,e);//栈,要转换的进制,元素 cout<<endl<<endl<<endl; }return 0;
}
status initlist(sqstack &s){//初始化 s.base=new int[MAXSIZE];if(!s.base) return error;s.top=s.base;s.stacksize=MAXSIZE;return ok;
}
void conversion(sqstack &s,int y,int e){//万物皆可十进制 x原先进制,y要转换的进制,m数值 while(e){push(s,e%y);e=e/y;}cout<<"转换成"<<y<<"进制为:";while(!stackempty(s)){pop(s,e);cout<<e;}
}
void input(int x,int &e){char a[20];scanf("%s",a);int c;c=strlen(a);cout<<endl;for(int i=0;i<c;i++){if(a[i]>='0'&&a[i]<='9')e+=((int)a[i]-48)*(int)pow(x,c-i-1);if(a[i]>='A'&&a[i]<='Y')e+=((int)a[i]-55)*(int)pow(x,c-i-1);}
}
void push(sqstack &s,int e){if(s.top-s.base==s.stacksize){cout<<"失败,栈满";}*s.top++=e;
}
int stackempty(sqstack s){if(s.top==s.base) return ok;return error;
}
int pop(sqstack &s,int &e){if(s.top==s.base) return error;e=*--s.top;return ok;
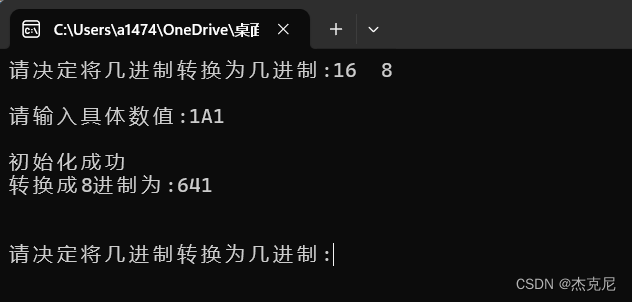
}4运行结果:









)


房地产消费者问卷调查)





)
