【笔试】01

1

给定一个 R 行C 列的二维数组 M 表示一张棋盘地图
数组元素取值为 0或者 1,1 表示对于的地图格子里有一颗炸弹,如下示例
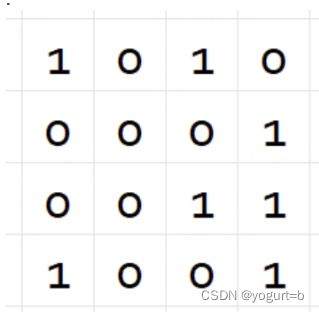
在这里插入图片描述

游戏规则如下:
1)当点击格子时,如果格子有炸弹(数值1),则炸弹发生爆炸
2)当一个格子中的炸弹爆炸时,其周围的8个格子(上,下,左,右,左上,左下,右上,右下)里如果有炸弹则会发生连锁反应一起爆炸
请问:最少需要点击几次可以清理完地图中所有炸弹?(如上图示例需要3次)
示例输入

[[1, 0, 0, 1],[0, 1, 1, 0],[0, 0, 1, 0],[1, 0, 0, 1]]

示例输出

解答

DFS
对于棋盘上的每一个格子，如果它包含炸弹（即值为1），我们就执行一次DFS，以模拟炸弹爆炸导致的连锁反应。DFS的过程中，我们会标记所有被连锁反应引父的炸弹，以确保每个炸弹只被计算一次。

    void dfs(vector<vector<int>>& M, int r, int c) {int R = M.size();int C = M[0].size();// 如果越界或者当前格子不含炸弹，则停止当前方向的搜索if (r < 0 || r >= R || c < 0 || c >= C || M[r][c] != 1) {return;}// 标记当前格子的炸弹已经爆炸（或者说，已经处理过），以避免重复计算M[r][c] = 0;// 搜索当前格子周围的8个方向dfs(M, r-1, c);   // 上dfs(M, r+1, c);   // 下dfs(M, r, c-1);   // 左dfs(M, r, c+1);   // 右dfs(M, r-1, c-1); // 左上dfs(M, r-1, c+1); // 右上dfs(M, r+1, c-1); // 左下dfs(M, r+1, c+1); // 右下}int minClicks(vector<vector<int>>& M) {int R = M.size();int C = M[0].size();int clicks = 0;for (int r = 0; r < R; ++r) {for (int c = 0; c < C; ++c) {if (M[r][c] == 1) {// 对于每一个未被爆炸的炸弹，执行一次DFSdfs(M, r, c);clicks++; // 每次DFS都代表了一次点击}}}return clicks;}

2

1)假如有A,B两个任务,如果要完成任务B必须先完成任务A,我们称A为B的前置任务, B为A的后置任务.
2)一个任务可以有最多2个(0个,1个,或者2个)的后置任务
3)后置任务不会再有后置任务
4)所有任务只能完成一次
问题:在给定玩家当前活力值 V,和当前游戏可做任务列表T的情况下,求通玩家过完成任务能获取的最高奖励.
输入描述
int V;玩家当前活力值vector<vector>T;当前游戏可做任务列表列表中的每一项为一个长度为 3的 vector表示一个任务的 3 个属性:[消耗活力值,任务奖励,其依赖的前置任务序号(序号-1表示无依赖前置任务)]
如:
0:[20,60，4]// 任务0,需要活力值20,完成任务可获得奖励60，依赖任务4
1:[20,60，4]// 任务1,需要活力值20,完成任务可获得奖励60，依赖任务4
2:[10,30，-1]// 任务2,需要活力值10,完成任务可获得奖励30，无依赖任务
3:[10,20，-1]// 任务3,需要活力值20,完成任务可获得奖励60，无依赖任务
4:[10,10，-1]// 任务4,需要活力值20,完成任务可获得奖励60，无依赖任务
示例输入

50,[[20,60,4],[20,60,4],[10,30,-1],[10,20,-1],[10,10,-1]]

示例输出

解答（存疑）

1、贪心-》寻找可能最优解

// 自定义排序函数，优先比较奖励，其次比较消耗活力值
bool compare(const vector<int>& a, const vector<int>& b) {double ratioA = (double)a[1] / a[0];double ratioB = (double)b[1] / b[0];return ratioA > ratioB;
}int getMaxReward(int V, vector<vector<int>>& T) {vector<bool> completed(T.size(), false); // 标记任务是否完成int totalReward = 0;// 分两轮处理任务：第一轮处理无依赖任务，第二轮处理有依赖的任务for (int round = 0; round < 2; ++round) {// 根据奖励/消耗比进行排序sort(T.begin(), T.end(), compare);for (int i = 0; i < T.size(); ++i) {if (completed[i]) continue; // 跳过已完成的任务int cost = T[i][0], reward = T[i][1], dependency = T[i][2];// 检查是否可以执行当前任务if (V >= cost && (dependency == -1 || completed[dependency])) {V -= cost; // 消耗活力值totalReward += reward; // 增加奖励completed[i] = true; // 标记任务为已完成}}}return totalReward;
}

2、回溯搜索，比较所有情况获得确定的最优解

int calculateMaxReward(const int V, vector<vector<int>>& tasks, vector<bool>& visited, int currentReward, int index, vector<int>& dependencyCounter) {if (index == tasks.size()) {// 所有任务都尝试过，返回当前奖励return currentReward;}// 直接跳过当前任务，看下一个任务的选择会如何int maxReward = calculateMaxReward(V, tasks, visited, currentReward, index + 1, dependencyCounter);// 尝试选择当前任务if (!visited[index] && V >= tasks[index][0] && (tasks[index][2] == -1 || (tasks[index][2] != -1 && visited[tasks[index][2]]))) {visited[index] = true; // 标记为已访问// 更新依赖计数器，对于任何依赖此任务的任务，减少它们的依赖计数for (int i = 0; i < tasks.size(); ++i) {if (tasks[i][2] == index) {dependencyCounter[i]--;}}// 选择当前任务，并递归尝试后续任务maxReward = max(maxReward, calculateMaxReward(V - tasks[index][0], tasks, visited, currentReward + tasks[index][1], index + 1, dependencyCounter));// 回溯，撤销当前选择visited[index] = false;for (int i = 0; i < tasks.size(); ++i) {if (tasks[i][2] == index) {dependencyCounter[i]++;}}}return maxReward;
}int getMaxReward(int V, vector<vector<int>>& tasks) {vector<bool> visited(tasks.size(), false); // 记录任务是否已完成vector<int> dependencyCounter(tasks.size(), 0); // 记录每个任务有依赖的次数for (auto& task : tasks) {if (task[2] != -1) {dependencyCounter[task[2]]++;}}return calculateMaxReward(V, tasks, visited, 0, 0, dependencyCounter);
}

3

能量站初始能量为0。
初始存在12个充能电池，每个电池具有各自的电能X(X为整数,4 <=X<=15)
每次给能量站注入能量需使用3个电池，同时要求3个电池的电能总和为4的整数倍
每天最多给能量站注入一次能量,单次注入的能量为(3个电池电能总和/4)的平方
电池使用后电能耗尽,同时不可再次使用
从今天开始每天使用电池给能量站注入能量，允许当天不使用任何电池给能量站注入能量，当天未使用的电池,若电能大于4，则电能将减少1，请输出在所有电池电能耗尽的情况下给能量站注入的最大的能量总和
输入描述
输入12个整数，空格隔开，表示12个电池各自的初始电能 4 <=X<= 15
输出描述
给能量站注入的能量总和的最大值
示例输入