异步FIFO设计的仿真与综合技术（3）

概述

本文主体翻译自C. E. Cummings and S. Design, “Simulation and Synthesis Techniques for Asynchronous FIFO Design 一文，添加了笔者的个人理解与注释，文中蓝色部分为笔者注或意译。前文链接：

异步FIFO设计的仿真与综合技术（2）https://blog.csdn.net/apple_53311083/article/details/132856486?spm=1001.2014.3001.5502 我们继续书结上回，来学习为什么异步FIFO中格雷码的使用

3.0 格雷码计数器（Gray code counter）

格雷码是以Frank Gray的名字命名的，他在1953年最初申请该编码专利，设计一个格雷码计数器有多种方法。本节详细介绍了一种简单而直接的设计方法。本文中描述的技术只使用了一组触发器作为格雷码计数器，第二种使用两组触发器来实现更高速度的方法在第4.0节中展示。

3.1 格雷码模式（Gray code patterns）

我们希望同时创建一个n位格雷码计数器和一个（n-1）位格雷码计数器（原因后面会说）。分别创建两个计数器当然很容易，但是创建一个通用的n位格雷码计数器，然后修改第二个MSB,通过共享LSBs构成一个（n-1）位格雷码计数器也是很容易和高效的。在本文中，这种方法被称为“双n位格雷码计数器”（dual n-bit Gray code counter）。

为了更好地理解将n位格雷码转换为（n-1）位格雷码的问题，我们考虑创建一个双4位和3位格雷码计数器的示例，如图2所示。

最常见的格雷码，如图2所示，是一个反射（reflected）编码，其中除了MSB位之外，任何列中的位都关于序列中点对称。这意味着4位格雷码的后半部分是MSB倒置的前半部分的镜像。

要把一个4位格雷码转换到3位，我们不希望4位序列的后半部分的LSBs是前半部分的LSBs的镜像，相反，我们希望后半部分的LSBs重复前半部分的4位LSBs。

经过更仔细的检查，很明显，反转4位格雷码的后半部分的第二个MSB（第二高位，这里指的就是从右往左数第二位）将在4位序列的三个LSB中产生所需的3位格雷码序列。唯一的问题是，具有额外MSB的3位格雷码不再是真正的格雷码，因为当序列从7（格雷码0100）改为8（~格雷码1000），再从15（~格雷码1100）改为0（格雷码0000）时，两位变化而不是一位。一个真正的格雷码在相邻数据之间只改变一位（这部分内容结合上面的图二应该解释的比较清楚）。

3.2 格雷码计数基础（Gray code counter basics）

关于格雷码，我们首先要明确的就是：任意两个相邻数之间的代码距离只有1（从一个格雷码变到相邻的另一个格雷码的时候，只有一个位可以改变）。第二点需要明确的是：当计数总量为2的幂次时，格雷码计数最有效。可以制作一个计数偶数个序列的格雷码计数器，但对这些序列的转换通常不像标准的格雷码那么简单。还要注意，没有计数奇数的格雷码计数器，所以人们不能制作一个计数值为23的格雷码代码。基于此，本文所设计的FIFO的深度被设置为 $2^{n}$ 。

图3是一个样式为#1的双n位格雷码计数器的框图。样式#1格雷码计数器假设寄存器位的输出是格雷码值本身（ptr、wptr或rptr）。格雷码输出被传递到格雷码-二进制转换器（bin），bin被传递到一个条件二进制值递增器以生成下一个二进制计数值（bnext），bnext被传递到二进制-格雷码转换器，该转换器生成下一个格雷码计数值（gnext），gnext被传递到寄存器输入。图3方框图的上半部分表示了所描述的逻辑流，而下半部分表示了下一节中描述的第二个格雷码计数器相关的逻辑。

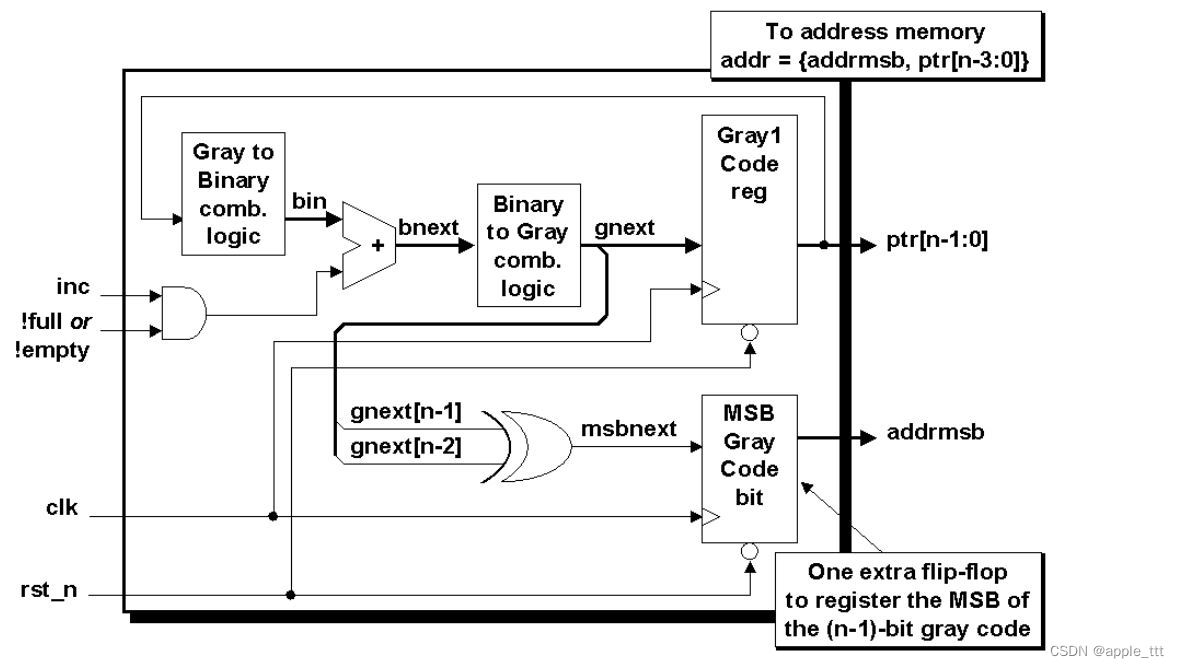
3.3 双n位格雷码计数器（Dual n-bit Gray code counter）

双n位格雷码计数器同时生成n位格雷码序列（见第3.2节所述）和（n-1）位格雷码序列。

（n-1）位格雷码只是通过对n位格雷码的两个MSB进行异或操作来生成，以生成（n-1）位格雷码的MSB。这与n位格雷码计数器的（n-2）个LSBs结合起来，形成（n-1）位格雷码计数器。

这里我们来简单解释一下，从3.1节中，我们知道，n-1位格雷码的生成方式是把格雷码的下半部分（MSB为1的部分）的第二高位（第二个MSB）翻转（0变1，1变0），这里我们的gnext[n-1]其实就是我们的MSB（在这里甚至可以直接理解成就是1），gnext[n-2]就是我们的第二个MSB，也就是gnext[n-2]与数据1进行异或操作，我们知道0和1异或结果是1，1和1异或结果是0，也就完成了第二高位的翻转，然后与剩下的LSBs进行拼接，就得到了n-1位的格雷码。

3.4 关于格雷码计数器的额外注意事项（Additional Gray code counter considerations）

二进制值递增器采用“如果未满”或“如果未空”测试，以确保适当的FIFO指针在FIFO满或FIFO空条件期间不会增加。

如果在生效FIFO满条件时，向FIFO发送数据的逻辑块能可靠地停止发送数据，则可以通过从FIFO写指针中删除FIFO满测试逻辑来简化FIFO设计。

FIFO指针本身并不保护FIFO缓冲区被覆盖（写覆盖，在写过数据的地方继续写，覆盖原有的数据），但是FIFO额外的条件逻辑可以被添加到FIFO内存缓冲区，以确保在FIFO满状态下写使能信号不能被激活。

可以向指针设计中添加一个附加的“sticky”状态位，即ovf（overflow,溢出）或unf（underflow,下溢出），以指示在FIFO满期间发生额外的FIFO写操作或在FIFO空期间发生额外的FIFO读操作，以指示只有通过复位才能清楚的错误情况。

一个安全、通用的FIFO设计将包括上述的保障措施，代价是稍大和可能较慢的实现。这是一个好主意，因为未来的同事可能会尝试在另一个设计中复制和重用代码，而不理解当前设计中所考虑的所有重要细节。

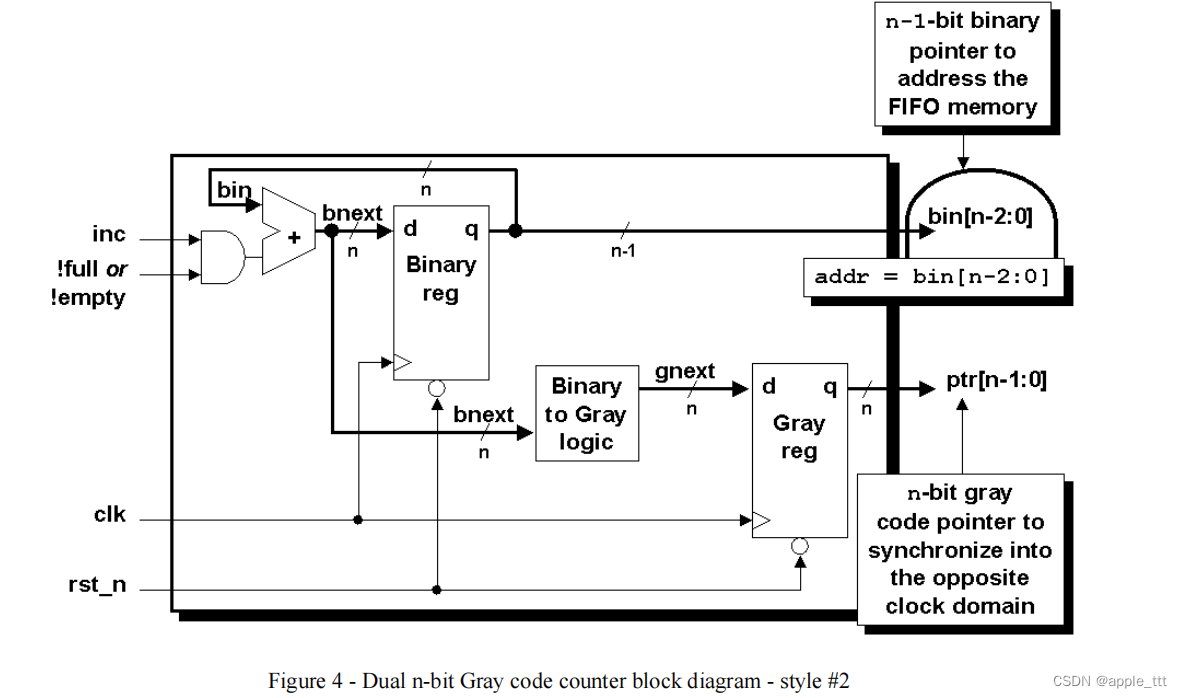
4.0 格雷码计数器-风格2（Gray code counter - Style #2）

从本文的1.2版本开始，FIFO实现使用了格雷码计数器-样式#2，它实际上使用了两组寄存器来消除将格雷码指针值转换为二进制值的需要。第二组寄存器（二进制寄存器）也可以用于直接寻址FIFO存储器，而不需要将存储器地址转换为格雷码。n-位的格雷码指针仍然需要将指针同步到相反的时钟域，但是n-1位的二进制指针可以直接用来处理内存。二进制指针还使运行计算更容易，以生成“几乎满”和“几乎空”的位（在本文中没有显示）。