文章目录
- 参考
- 概述
- 软件工程概述
- 软件过程
- 可行性分析
- 可行性分析概述
- 数据流图
- 数据字典
- 需求分析
- 需求分析概述
- ER图
- 状态转换图
参考
软件工程速成(期末+考研复试+软考)均适用. 支持4K
概述
软件工程概述
定义:采用工程的概念、原理、技术和方法来开发与维护软件。
三要素:
- 方法:完成软件开发各项任务的技术方法,回答“怎么做”。
- 工具:为运用方法提供的自动或半自动软件工程支撑环境。
- 过程:为了获得高质量软件所需要完成的一系列任务框架,回答“什么时候做”
软件生命周期三时期、八阶段。
- 软件定义时期。包括的阶段有:
问题定义阶段:用户需要解决什么样的问题。
可行性研究阶段:软件开发是否可行。
需求分析:明确客户需求,输出标准化的需求说明书。 - 软件开发时期,包括的阶段有:
总体设计:设计整体结构、确定综合测试目标
详细设计
编码和单元测试
综合测试 - 软件维护时期(持续时间最长、花费最大)
软件运维
软件过程
主要包括瀑布模型、增量模型、螺旋模型、喷泉模型等,是任务框架。
-
瀑布模型
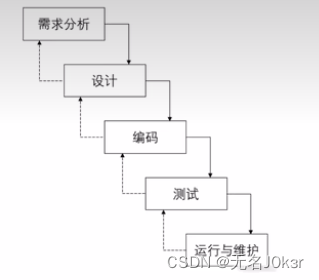
特点:是最基本的软件开发生命周期模型。
优点:方便组织管理,提高了大型软件开发的质量和效率。
缺点:开发过程死板,不便修改,很难实践 -
增量模型
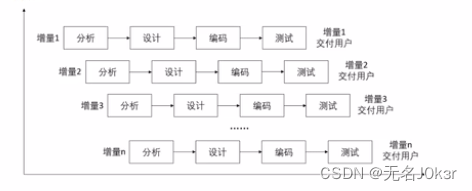
优点:人员分配灵活、可先发布部分功能给客户。
缺点:并行开发有难以集成的风险。 -
螺旋模型
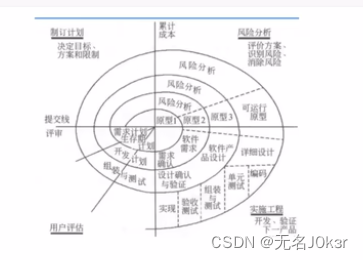 特点:引入了风险分析,每个螺旋周期大致是瀑布模型。
特点:引入了风险分析,每个螺旋周期大致是瀑布模型。
优点:设计灵活,方便变更、每个周期均要求用户评估。
缺点:迭代次数太多导致成本高。 -
喷泉模型
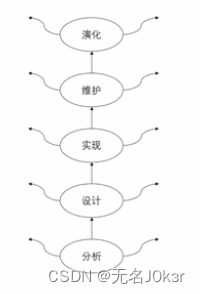
特点:划分为多个阶段,但无明显界限,可迭代交叉。
可行性分析
可行性分析概述
可行性分析:用最小代价在最短时间内确定问题是否可解决。
可行性研究:了解客户要求,从技术、经济、社会因素等方面论证可行性
数据流图
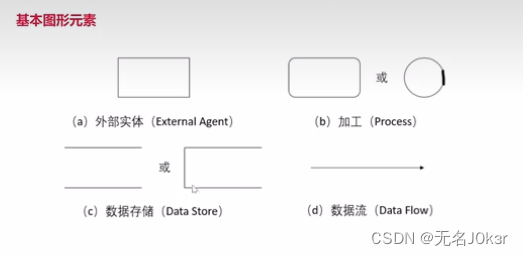
数据流图也称为数据流程图DFD,是一种便于用户理解、分析系统数据流程的图形工具,其基本元素包括:
- 外部实体:表示数据的源点和终点,为软件系统外的人员或组织。
- 加工:数据的处理。
- 数据存储:信息的静态存储。
- 数据流:转移了什么数据。
例题:零件入库或出库称为事务,通过放在仓库中的CAT终端把出入库事务报告给订货系统。当某种零件的库存数小于阈值时应该再次订货。采购部每天需要一张订货报表,报表按零件编号排序,表中列出所有需要再次订货的零件,这些零件具有如下数据(零件编号、零件名称、订货数量、目前价格、主要供应商、次要供应商)。
解题:
一、从问题描述中提取数据流的四种成分
- 源点和终点:通过仓库的CAT终端把事务报告给订货系统,进而到采购部,源点是仓库管理员,终点是采购人员。
- 加工:采购部需要订货报表,因此需要生成订货报表。出入库改变零件数量也是一个加工。
- 数据流:一是从仓库把出入库事务报告给订货系统,二是订货报表送到采购部。
- 数据存储:需要订货的零件的信息、库存信息。
二、画大致模型
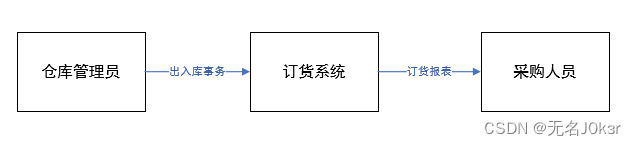
三、进一步细化
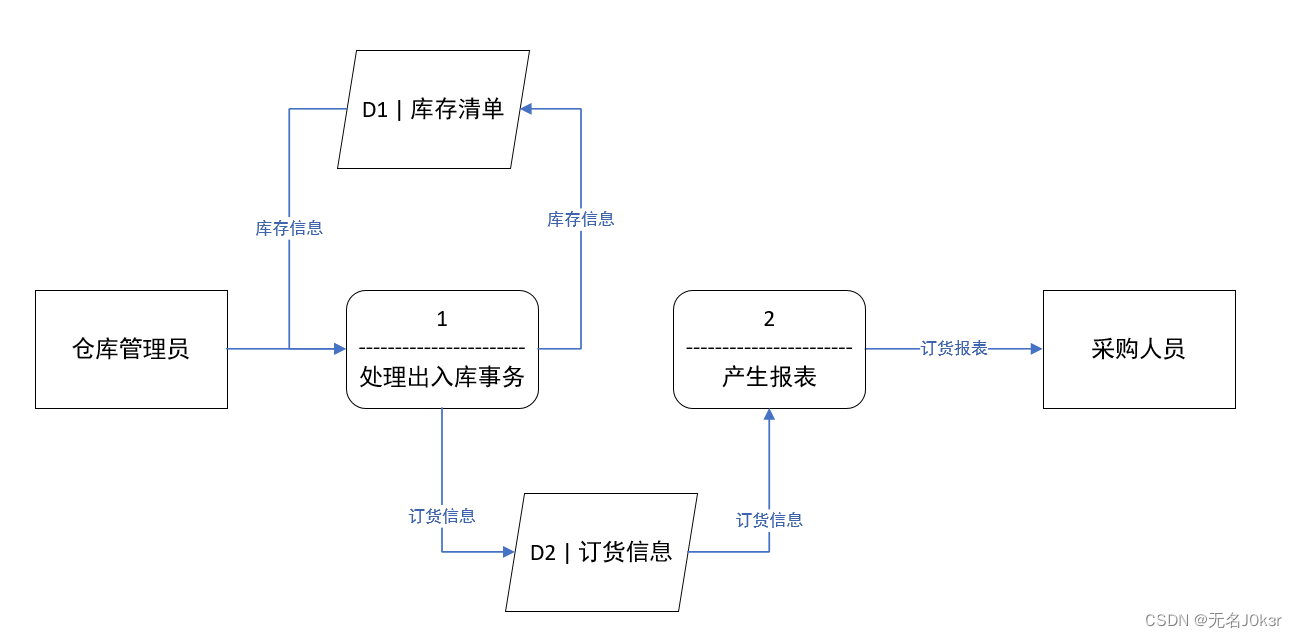
数据字典
数据流图描述了系统的分解,数据字典用于为数据流图中的每个数据流、文件、加工、数据项等作出说明,有以下四类条目:
- 数据流条目:描述数据组成部分(如:内部号码=非零数字+3{数字}3)
- 数据存储条目:
- 数据项条目:
- 处理条目:
需求分析
需求分析概述
定义:需求分析是指开发人员要准确理解客户要求,进行详细调查研究,将用户的非形式话的需求描述转换为完整的需求定义,进而生成软件需求规格说明书的过程。
ER图
提供了表示实体类型、属性和联系的方法。
状态转换图
通过描绘系统状态及引起系统状态转换的事件,来表示系统的行为,其符号包括:
- 初态:用实心圆表示。
- 中间状态:用圆角矩形表示,可分为上中下三部分,分别代表状态的名称、变量说明(可选)和活动表(可选)。
- 终态:用一对同心圆表示。
- 状态转换:用箭头表示。如转换由事件触发则应在箭头上标明,不标明则表示在原状态内部活动执行完之后自动触发。
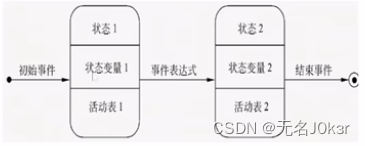



是什么意思)
:Harris角点检测)
)
)



玩转正则表达式等常用API)








