1 机器学习中的建模
1.1 描述性建模
以方便的形式给出数据的主要特征,实质上是对数据的概括,以便在大量的或有噪声的数据中仍能观察到重要特征。重在认识数据的主要概貌,理解数据的重要特征。
- Task:聚类分析,数据降维,流形学习,密度估计,异常分析,可视化
1.2 预测性建模
以函数的形式给出感兴趣量(预测量)与可观测量之间的数量关系,实质上是根据观测到的对象特征来预测对象的其他特征。重在把握协变关系,据此进行预测。
- Task:分类(类别预测),回归(数值预测),评分(排名预测)
1.2.1 预测性建模方法
概率方法:生成式建模方法,借助训练数据对同类数据的生成机制(概率分布)进行估计,基于概率关系对变量取值进行概率预测。把模式视为随机变量的抽样,利用统计决策理论(贝叶斯统计)成熟的判决准则与方法,对模式样本进行分类
如:贝叶斯分类器、贝叶斯网络(概率图模型)、高斯混合模型、隐马尔可夫模型、受限玻尔兹曼机、生成对抗网络,变分自动编码器
代数方法:判别式建模方法,借助训练数据对观测量和预测量的函数关系进行直接建模,基于函数关系对变量取值进行数值预测。利用向量空间的直观概念,使用代数方程方法,对模式进行分类
如:KNN,感知机,判别分析,决策树,随机森林,支持向量机、逻辑回归,神经网络
1.3 判别函数
1.3.1 线性可分概念与线性分类算法
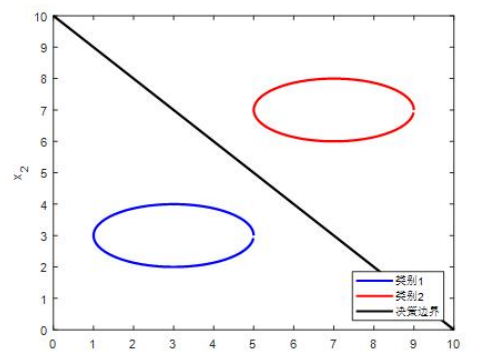
一个分类问题是否属于线性可分,取决于是否有可能找到一个点、直线、平面或超平面来分离开两个相邻的类别。如果每个类别样本的分布范围本身是全连通的单一凸集,且互不重叠,则这两个类别一定是线性可分的,如图所示。线性分类算法主要有线性判别函数、Fisher判别分析、单层感知器、逻辑回归等
1.3.2 判别函数的定义
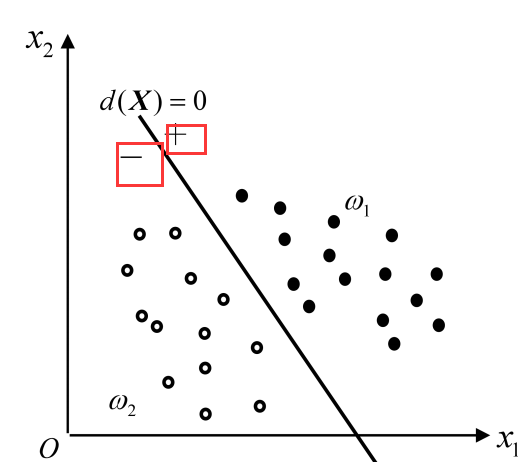
直接用来对模式进行分类的决策函数,若分属于ω1,ω2两类的n维模式在空间中的分布区域,可以用一代数方程d(X) =0决定的超平面作为分隔面,两类样本分布在分隔面的两侧,那么就称d(X)为判别函数(discriminant function)或称决策函数(decisionfunction)。代数方程d(X) =0表示的是n维空间的(n-1)维判决面 {或超平面(hyperplane)或超曲面(hypersurface) ,视d(x)形式而定}。
Note:这里的模式或许可以直接理解成数学里的自变量。
为了清晰地了解d(x)的含义,应该画出判别函数值d(x)这一轴,在没有画出的时候,就在自变量(模式)空间中画出d(x)取正负值的区域——这就是所谓判别面的正侧、负侧。
1.3.3 确定判别函数的两个因素
- 判决函数d(X)的函数形式:它可以是特征的线性或非线性的函数。
- 判决函数d(X)的系数:用所给的模式样本,通过优化准则确定。
主要关注线性判别函数,一个一般的n元线性函数应该具有什么的性质才适合做两分类和多分类的判别函数
2 线性判别函数
2.1 两类问题
在两类别情况下,判别函数 g (x) 具有以下性质:
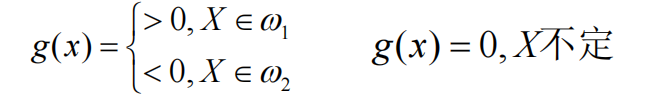
这是二维情况下判别由判别边界分类。情况如图:
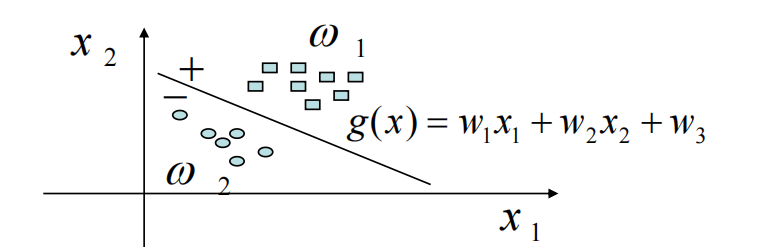
在n维情况下:
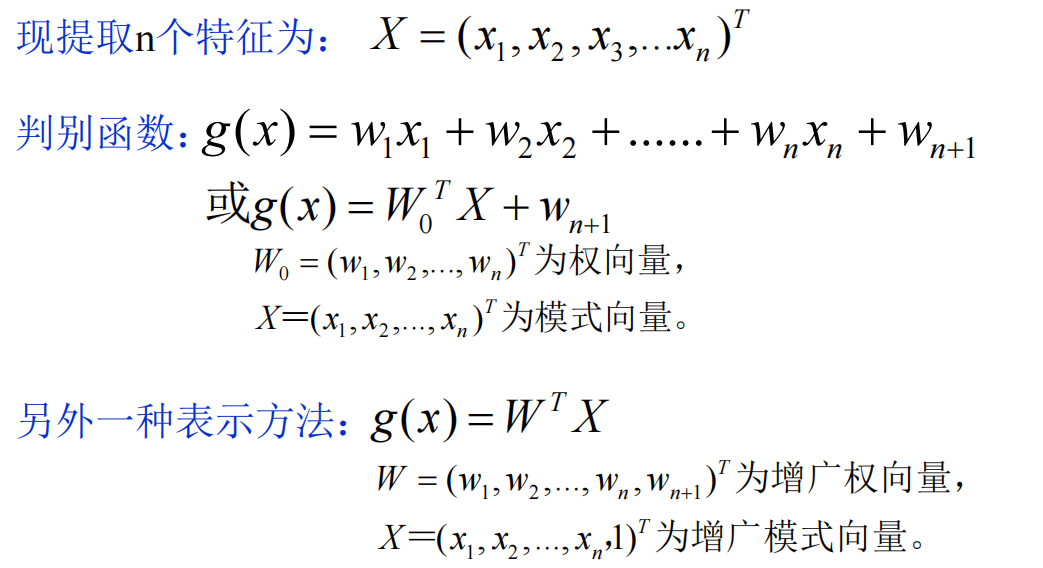
2.2 区别分类与回归两个概念
回顾:一元/多元线性回归(Multivariate linear regression)

w参数学习/训练出来之后,所确定的g(x)模型也叫预测模型。
若用g(x)预测的是离散值,此类学习任务称为“分类(Classification)” ;若用g(x)预测的是连续值,此类学习任务称为“回归(regression)”。由于这里g(x)是线性的,故称为多元线性回归
离散值预测->分类, 连续值预测->回归
2.3 多类问题
对于多类问题,模式有 ω1 ,ω2 , … , ωm 个类别。可分三种情况讨论:
2.3.1 ω i / ω ˉ i \omega_i / \bar{\omega}_i ωi/ωˉi多类情况1 (是非两分法)
每一模式类与其他模式类间可用单个判别平面把一个类分开。这种情况,M类可有M个判别函数,且具有以下性质:
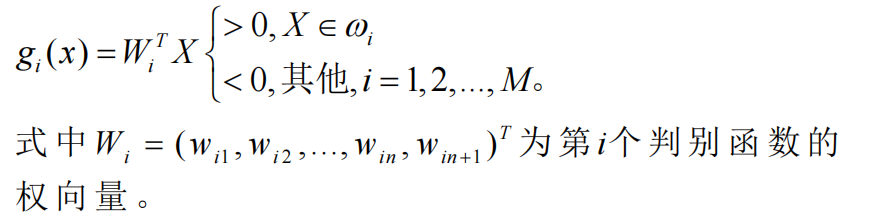
理解:
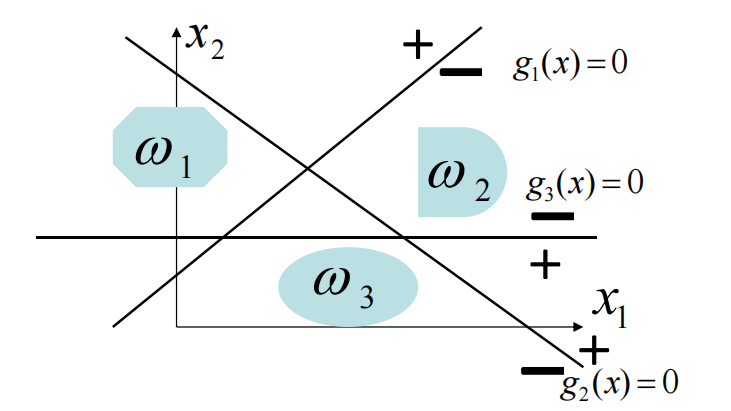
每一类别可用单个判别边界与其他类别分开。若一模式X属于ω1,则由图可清楚看出:这时g1(x) >0而g2(x) <0 , g3(x) <0 。 ω1 类与其他类之间的边界由g1(x)=0确定。模式属于哪一类,对应的那一类的判别函数值就大于0。
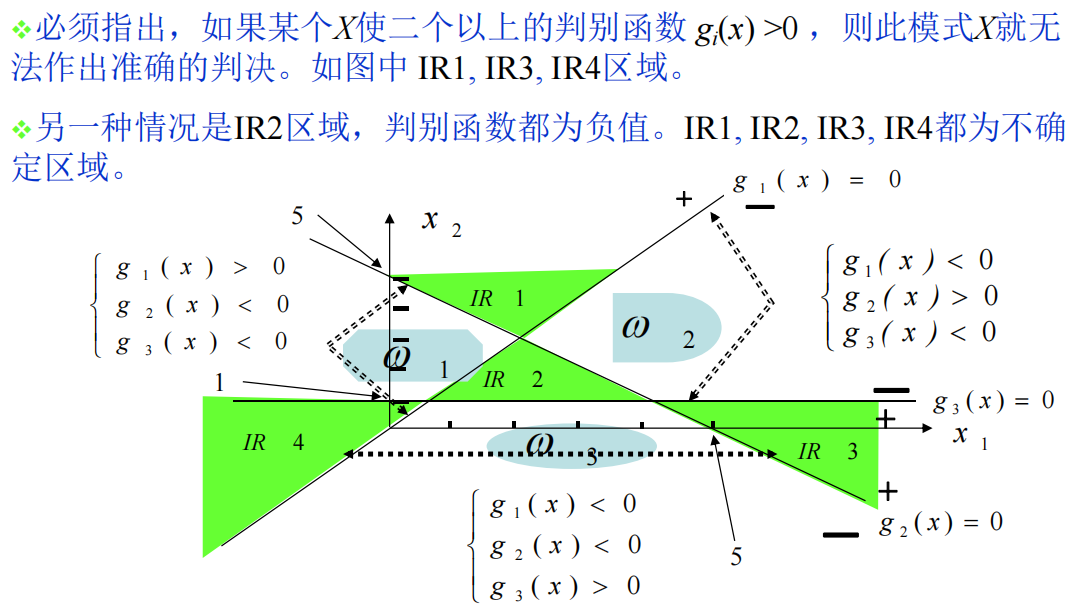
特殊情况:
2.3.2 ω i / ω j \omega_i / {\omega}_j ωi/ωj多类情况2(成对两分法)
每两个模式类间可用判别平面分开(即模式类成对可分)。

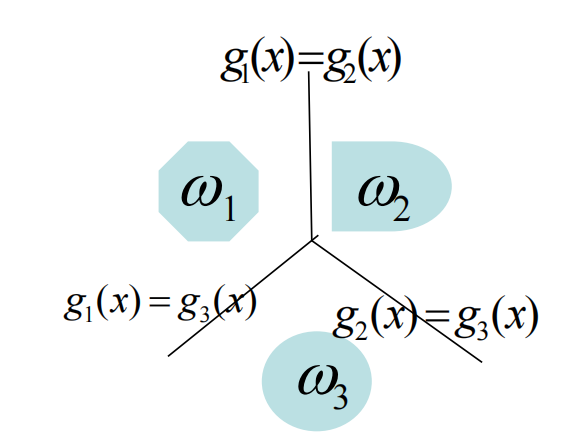
2.3.3 多类情况3: ω i / ω j \omega_i / {\omega}_j ωi/ωj 成对两分法(无IR区)

多类情况3下的一个示例:不存在IR区域,IR不确定区没有了,所以这种是最好的情况。
2.4 线性判别函数的性质
- 模式空间与加权空间:由于假设权向量W与模式向量X的内积为零(g(x)=0),故W与分界面H正交





 第三节 关系数据库标准语言SQL(Ⅳ))
:部署、使用 metrics-server)

)





--unity调试--长痛不如短痛)





