目录

【93.复原IP地址】中等题（偏难，坑很多）

【78.子集】中等题（偏简单）

【90.子集II】中等题

【93.复原IP地址】中等题（偏难，坑很多）

思路：以101023为例子

1、将题目抽象成树，子节点为指定开始索引start的子串，在遍历子节点的时候进行剪枝（打叉的地方表示剪枝），保证子节点合法

2、利用len指示IP的长度，如果已经够4个IP段，则处理结果。（图中是圆圈标注的是处理的结果，×表示长度够了，但是数组中数字没用完，不需要记录结果；√ 表示长度够了，数组中数字也用完了，得记录结果）

关键：重点考虑三个问题

• 剪枝1：如果当前子节点>255怎么办？当前及剩下的子节点不需要遍历，使用break跳出for循环
• 剪枝2：如果剩下的数字不足以构成4个IP段怎么办？当前及剩下子节点不需要遍历，使用break跳出for循环
• 剪枝3：如果当前子节点以0开头怎么办？只递归遍历单独"0"这个子串的分支，​遍历完后直接return，不再遍历剩下的"0x"不合法的IP段。​​​​​​（图中的方框处就是遍历单独的"0"）

class Solution {List<String> res = new ArrayList<>();StringBuffer path = new StringBuffer();public List<String> restoreIpAddresses(String s) {backtracking(s, 0, 0);return res;}// start是指当前层的所有子节点对应子串在数组中的开始索引// len是指当前层对应的IP段索引，从0开始，0-3对应4个IP段，当len - 4时，说明已经够4个IP段了，得考虑是否记录结果了public void backtracking(String s, int start, int len){// 终止条件(长度够了，判断 -> 数字用完了/数字没用完)if (len == 4){// 数组中的数字没用完if (start < s.length()) return; // 不记录，直接返回// 数组中的数字用完了else{// 这里不能直接删除path最后一个"."，否则回溯恢复现场的时候会出错String ss = path.toString();res.add(ss.substring(0, ss.length() - 1));  // 把最后一个"."删除，再记录结果return;}}// 单层递归逻辑// 遍历所有子节点(左闭右闭，i指示的是子串的结束索引，包含i)for (int i = start; i < s.length(); i++){String sub = s.substring(start, i+1); // 取子串是左闭右开// 剪枝1：使IP有效(如果当前子节点超过255，就不需要再遍历剩下的子节点)if (Integer.valueOf(sub) > 255) break;  // 注意是break，不是continue// 剪枝2：加速遍历(如果剩下的数字不足以构建剩下的IP段（path需要4个IP段），则不再遍历剩下的子节点)if (s.length() - i - 1 < 4 - len - 1) break;path.append(sub + ".");backtracking(s, i+1, len+1); // 当前子串i结束，那下个子串就从i+1开始path.delete(path.length() - sub.length() - 1, path.length()); // 把子串和"."一起删除// 剪枝3：使IP有效（可以是单独的0，但是不能是以0开头的其它整数）if (sub.startsWith("0")) return; // 如果字符串的开头是"0"，只需要把"0"的分支遍历完即可返回，其余的不合法}}}

总结：

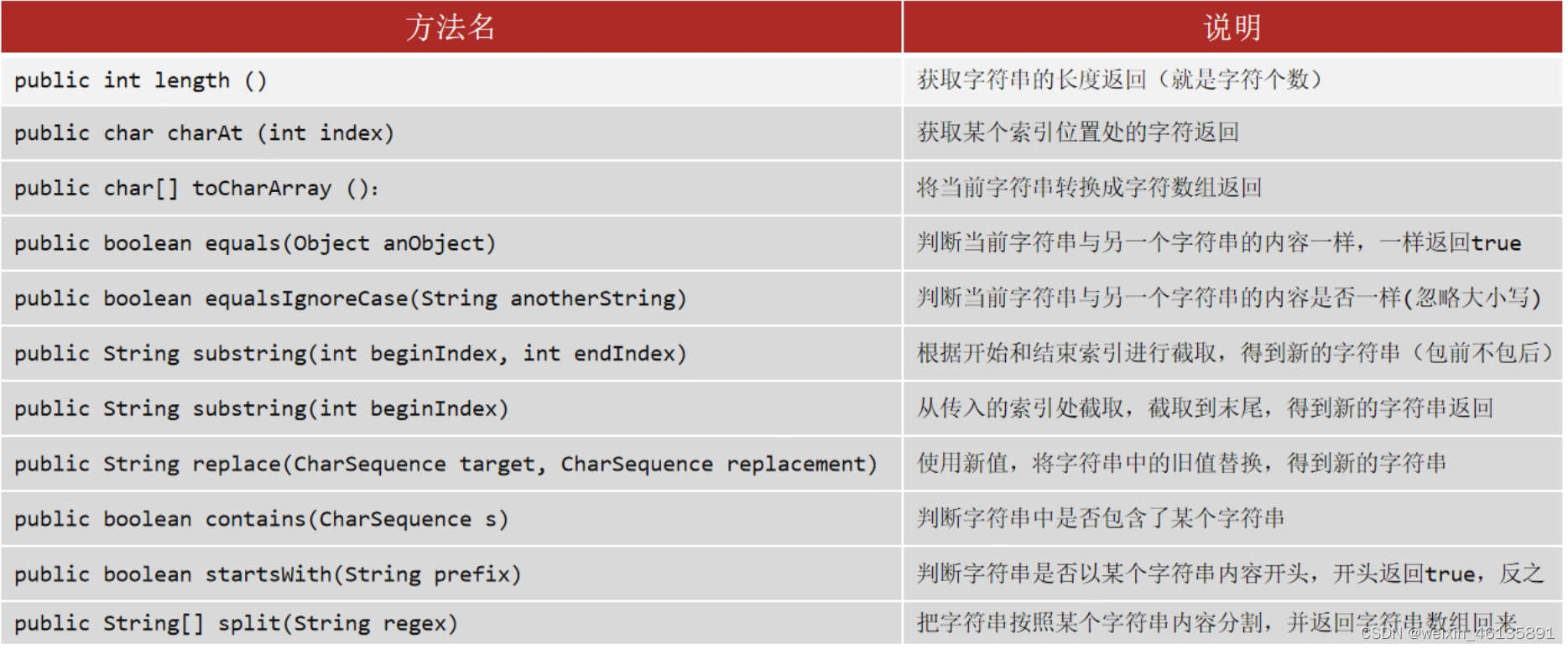
1、String类的常用方法

2、StringBuffer的常用方法

补充刷题常用的方法：

• 删除指定索引的字符：deleteCharAt(int index);
• 删除指定索引范围的字符串：delete(int start, int end);

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {res.add(new ArrayList(path)); // 加入空集backtracking(nums, 0);return res;}public void backtracking(int[] nums, int start){for (int i = start; i < nums.length; i++){path.add(nums[i]);res.add(new ArrayList(path));  // 每个子节点都需要记录路径backtracking(nums, i + 1);path.remove(path.size() - 1);}}
}

思路：和【78.子集】的区别在于，元素可以在数组中重复出现，需要先排序，后去重。

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> subsetsWithDup(int[] nums) {Arrays.sort(nums);  // 先对nums进行排序，便于后序的去重backtracking(nums, 0);  // 不需要再单独加入空集，因为一进入递归，当前节点对应路径就是空集return res;}public void backtracking(int[] nums, int start){// 记录当前节点对应的路径res.add(new ArrayList(path));for (int i = start; i < nums.length; i++){// 去重：如果当前层前面已经遍历过相同的子节点，就不再记录当前子节点对应路径和递归遍历当前子节点if (i > start && nums[i] == nums[i - 1]) continue;  // 注意是i > start，而不是i>0，i>0不能代表同一层的子节点path.add(nums[i]);backtracking(nums, i + 1);path.remove(path.size() - 1);}}
}

注意：去重的时候，是判断当前子节点在当前层前面是否已经遍历过，是 i > start， 而不是 i > 0。i > start才能保证判断的是当前层的第二个节点，而当前层的第一个节点也可能符合 i > 0，万一该节点等于数组中上一个节点的值，则该节点就无法遍历了。