卷积神经网络是一种多层的监督学习神经网络，隐含层的卷积层和池采样层是实现卷积神经网络特征提取功能的核心模块。卷积神经网络结构包括：卷积层，降采样层，全链接层。每一层有多个特征图，每个特征图通过一种卷积滤波器提取输入的一种特征，每个特征图有多个神经元。

一、卷积神经网络基础

   输入数据进入卷积层后，与卷积核进行运算，计算的结果就是得到的特征图。如果得到的特征图尺寸较大，我们可以采用池化层（降采样层）进行降采样，来减小特征图的尺寸。

1.卷积层

conv2d = nn.Conv2d(1, 1, kernel_size=3)   #输入通道1，输出通道1，卷积核为3*3  

（1）内部参数：卷积核权重

   当输入数据进入卷积层后，输入数据会与卷积核进行卷积运算。卷积核相当于权重系数。将卷积核与输入数据对应元素进行加权求和计算出结果。

kernel_size=3      """3*3的卷积核"""
kernel_size=(2,3)  """2*3的卷积核"""

具体计算步骤：

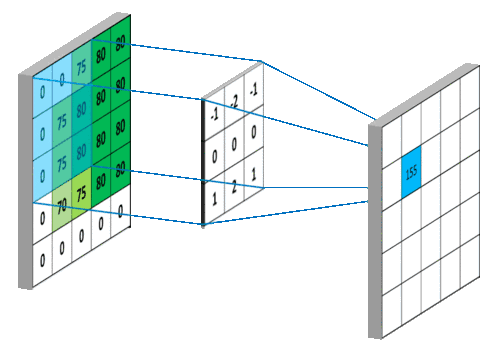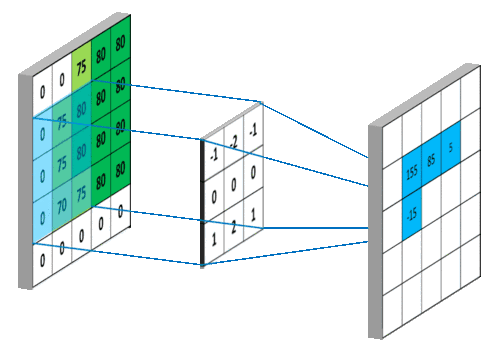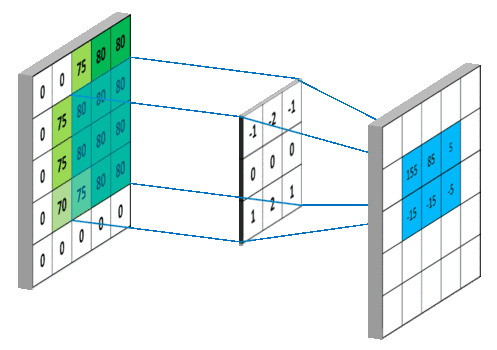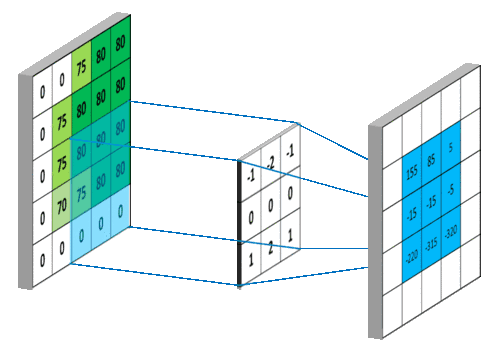
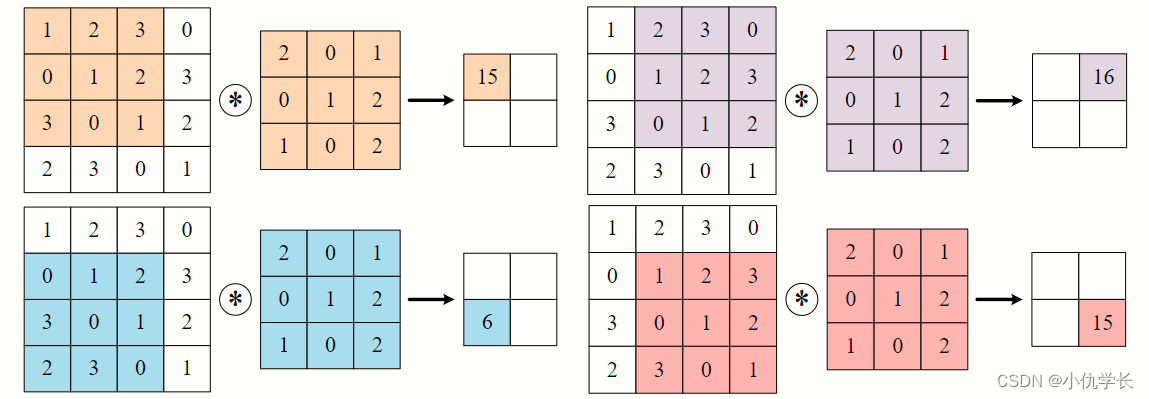
（2）内部参数：偏置

卷积层也会有偏置操作。

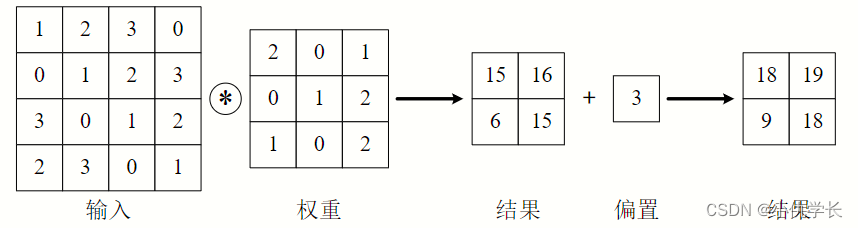
（3）外部参数：填充padding（默认不填充）

  为了防止经过多个卷积层后图像越卷越小，可以在进行卷积层的处理之前，向输入数据的周围填入固定的数据（比如 0），这称为填充（padding）。这样经过卷积后的图片不会变小，并且可以保留原始图像的边界信息，以便我们设计更深层次的神经网络。

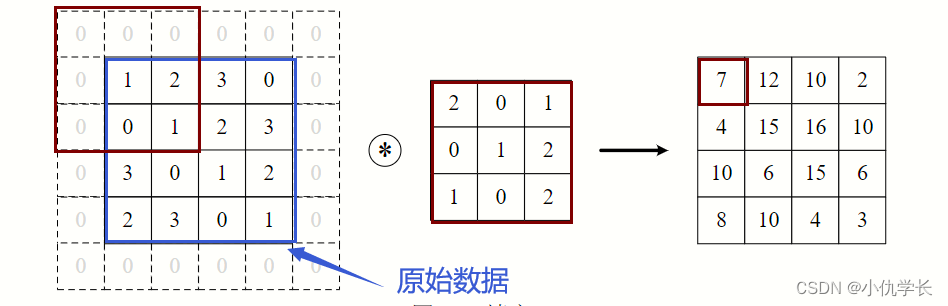
padding=1 ：输入元素上下左右各添加一圈0元素

"""(输入通道、输出通道、卷积核，填充层）"""
"""  padding=1    :输入元素上下左右各添加一圈0元素"""
"""kernel_size=3  :卷积核为3×3 """
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)  #举例：                           0  0  0  0  0  0
1  2  3  4                        0  1  2  3  4  0
5  6  7  8              		  0  5  6  7  8  0
9 10 11 12          		      0  9 10 11 12  0
13 14 15 16           		      0 13 14 15 16  00  0  0  0  0  0

padding=(0,1) ：输入元素上下维度不添加0，左右维度添加一圈0元素

"""padding=(0,1)      :输入元素上下维度不添加0，左右维度添加一圈0元素"""
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=(0,1))  #举例：
1  2  3  4                        0  1  2  3  4  0
5  6  7  8              		  0  5  6  7  8  0
9 10 11 12          		      0  9 10 11 12  0
13 14 15 16           		      0 13 14 15 16  0

padding=‘SAME’ ：在输入的周围添加足够的零填充，以确保卷积操作的输出尺寸与输入尺寸相同

 """padding='SAME '  即在输入的周围添加足够的零填充，以确保卷积操作的输出尺寸与输入尺寸相同"""
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding='SAME' )  

（3）外部参数：步幅stride（默认步幅为1）

  在卷积操作中，步幅（stride）是指卷积核在输入数据上滑动的步长。它决定了输出特征图的空间尺寸。
   具体来说，步幅控制了卷积核在输入数据的行和列方向上的移动距离。如果步幅为 1，那么卷积核将以一次一个像素的速度沿着输入数据的行和列方向滑动。而如果步幅为 2，则每次移动两个像素，以此类推。

stride=2 ：行列步幅都为2。

conv2d = nn.Conv2d(1, 1, kernel_size=2, stride=2)

如下：

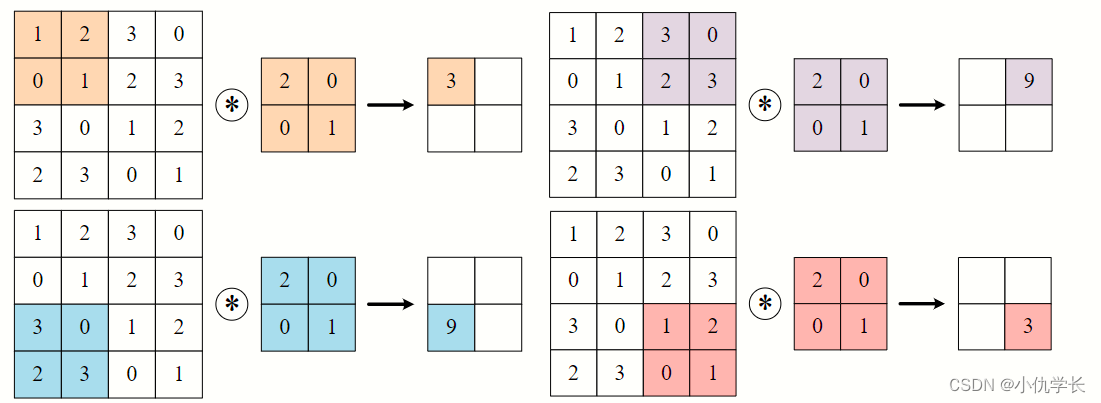
stride=(2,3) ：行步幅为2，列步幅为3。

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=1,  stride=(2,3))

  

2. 池化层（Pooling）

  池化层是卷积神经网络中的一种常用层，用于减少特征图的空间尺寸，从而减少参数数量并且降低模型的计算复杂度。池化操作通常应用于卷积层的输出之后，通过对局部区域进行汇聚（如取最大值或求平均值）来减小特征图的尺寸。
   池化层分为：最大池化和平均池化。

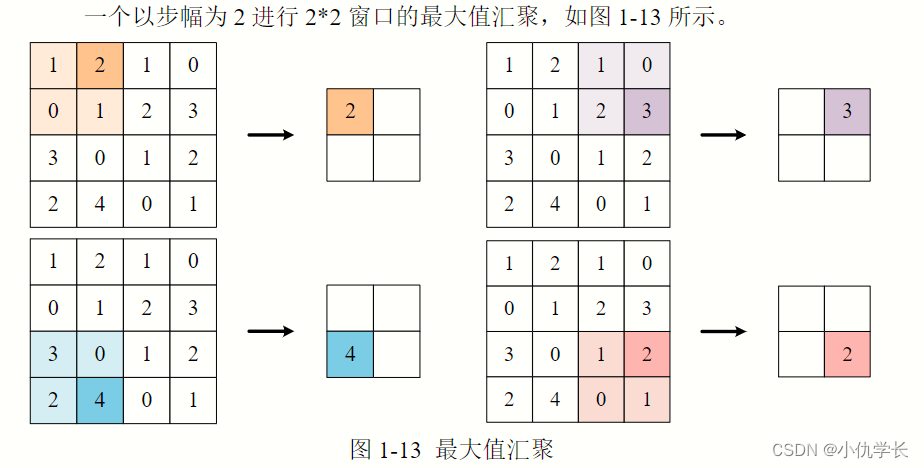
（1） 最大池化层

原理：取得原特征图窗口大小内元素的最大值作为新的特征图元素。

max_pool_layer = nn.MaxPool2d(kernel_size=2, stride=2)

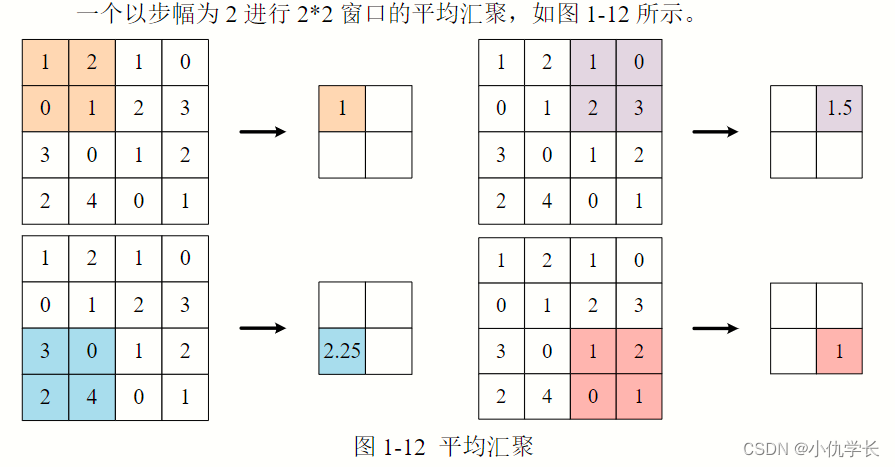
（2） 平均池化层

原理：取得原特征图窗口大小内元素的平均值作为新的特征图元素。

avg_pool_layer = nn.AvgPool2d(kernel_size=2, stride=2)

  

3. 滤波器–多通道卷积核

   上述的卷积层，仅仅针对二维的输入与输出数据（一般是灰度图像），可称之为单通道。但是，彩色图像除了高、长两个维度之外，还有第三个维度：通道（channel）。例如，以 RGB 三原色为基础的彩色图像，其通道方向就有红、黄、蓝三部分，可视为 3 个单通道二维图像的混合叠加。
   一般的，当输入数据是二维时，权重被称为卷积核（Kernel）；当输入数据是三维或更高时，权重被称为滤波器（Filter）。
   在卷积神经网络（CNN）中，滤波器用于提取图像中的特征。每个滤波器都可以看作是一个多通道的卷积核，因为它在图像的每个通道上进行卷积操作，并输出一个单通道的特征图。

（1）多通道输入

   对三维数据的卷积操作下图所示，输入数据与滤波器的通道数必须要设为相同的值，可以发现，这种情况下的输出结果降级为了二维特征图，也就是单通道。
   简单来说：输入数据有多少个通道就决定了一个滤波器有多少个通道。


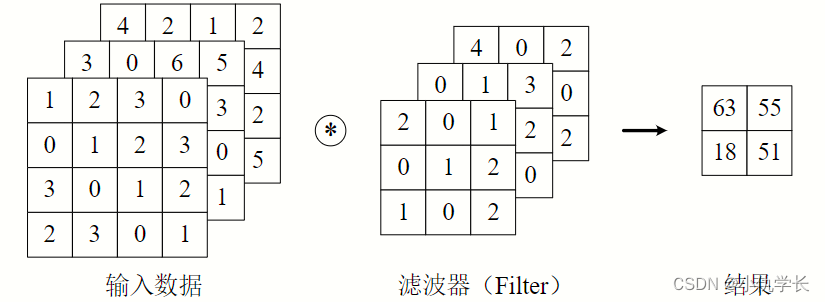
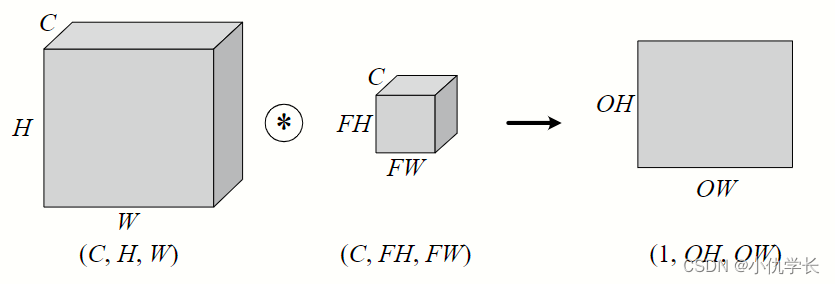
计算过程：

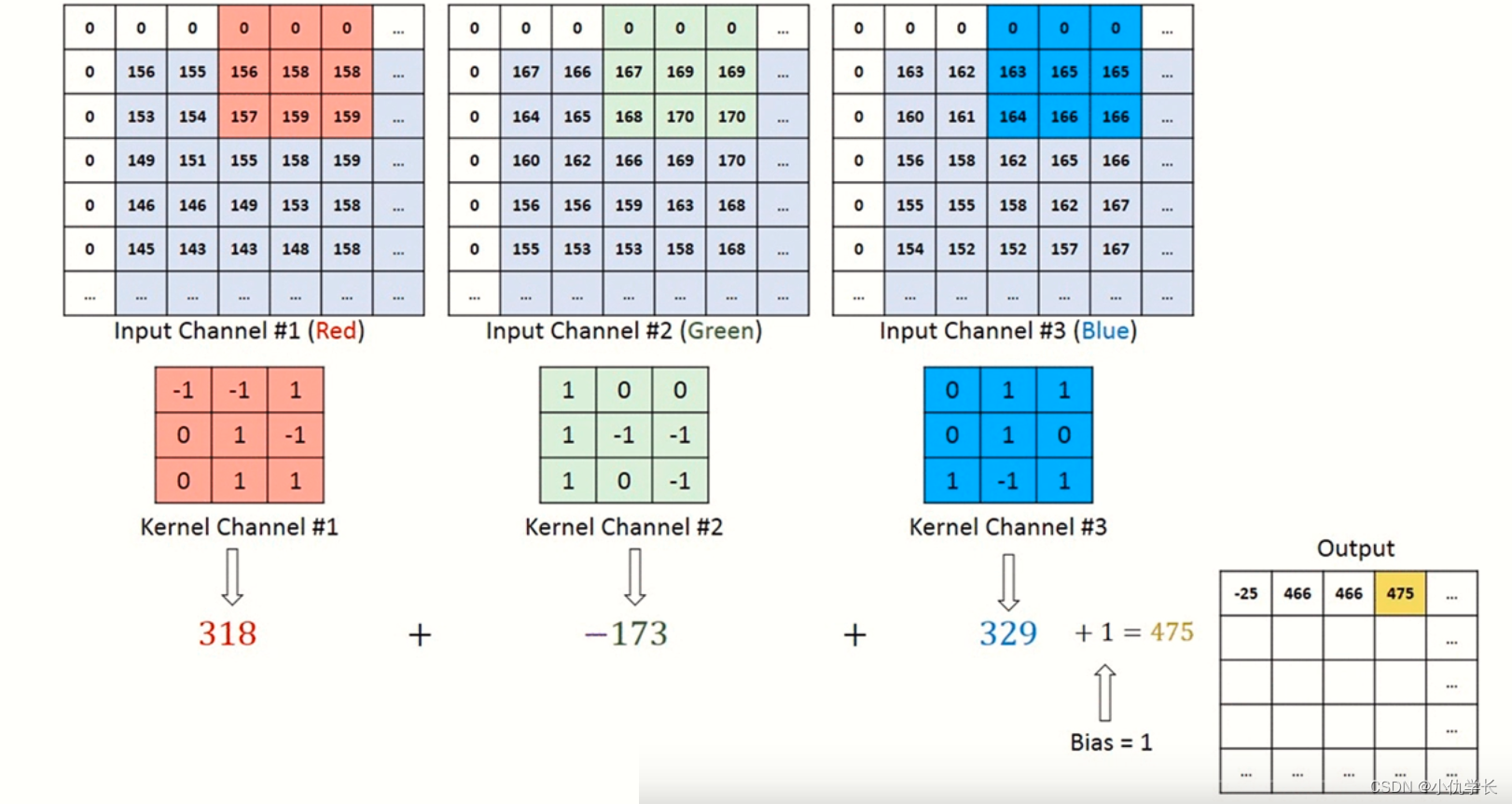
（2）多通道输出

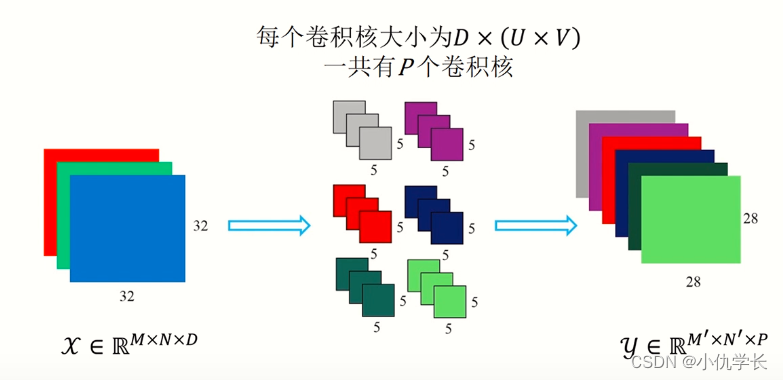
   当通过一个多层卷积核（滤波器）时，输出就被降成二维特征图了。大多数时候我们需要三维的特征图时就可以多经过几个滤波器，单个滤波器会生成单通道的特征图，多个滤波器就可以生成多个特征图，我们把这些多个特征图合并，就变成了多通道的特征图，因此就有了多通道输出。
   简单来说：有多少个滤波器（多通道卷积核），输出特征图就有多少个通道。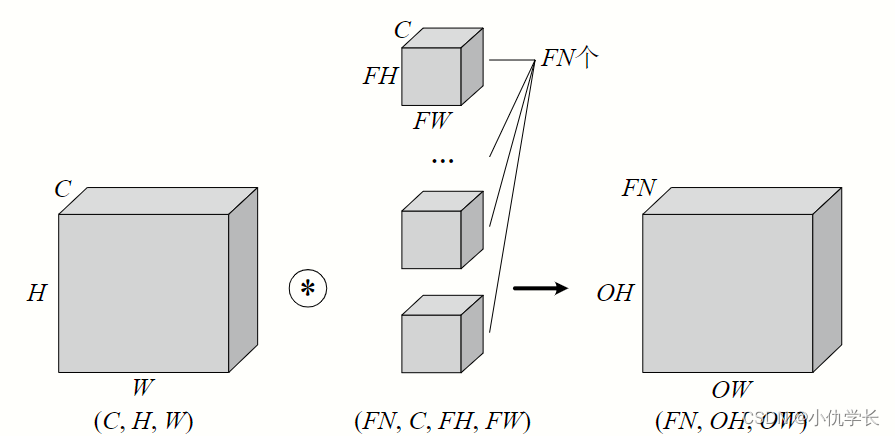

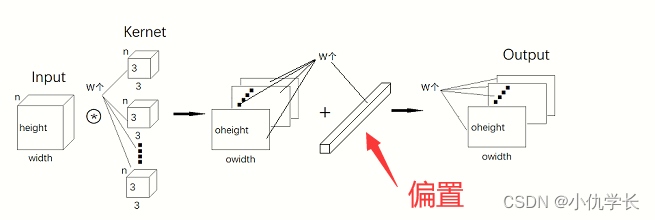
   别忘了，卷积运算中存在偏置，如果进一步追加偏置的加法运算处理，则结果如下图所示，每个通道都有一个单独的偏置。