题目链接

三角形最小路径和

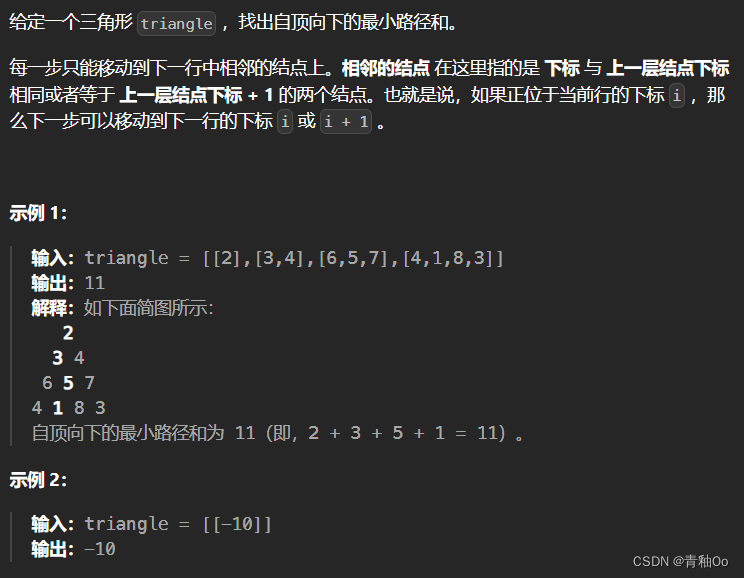
题目描述

注意点

• -10000 <= triangle[i][j] <= 10000
• triangle[i].length == triangle[i - 1].length + 1
• triangle[0].length == 1

解答思路

• 由题意得，到达任意第i层第j个节点的路径和一定是由第i - 1层第j - 1或第j个节点到达（边界除外），所以可以使用dp存储上一层节点的最小路径和，以推出下一层对应节点的最小路径和

代码

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int res = Integer.MAX_VALUE;int n = triangle.size();// 本层到达节点i时的最小路径和（根据上一层的节点推出）int[] dp = new int[n];// 第一层无上一层且只有一个节点dp[0] = triangle.get(0).get(0);for (int i = 1; i < n; i++) {// 深拷贝，dp会被新一层的节点覆盖int[] tmp = new int[i];for (int j = 0; j < i; j++) {tmp[j] = dp[j];}// 第i行有i + 1个元素List<Integer> list = triangle.get(i);// 首节点特殊考虑，无tmp[-1]dp[0] = tmp[0] + list.get(0);for (int j = 1; j < i; j++) {dp[j] = Math.min(tmp[j - 1], tmp[j]) + list.get(j);}// 尾节点特殊考虑，无tmp[i];dp[i] = tmp[i - 1] + list.get(i);}for (int i = 0; i < n; i++) {res = Math.min(res, dp[i]);}return res;}
}

关键点

• 动态规划的思想
• 注意边界问题
• 计算新一层最小路径和时会覆盖当前的dp，注意需要使用一个新的数组深拷贝记录旧的dp的值