话不多说,直接看题:

首先我们大致分析一下,先排序一下,K==n,那就全部选。
当k<n时,k是偶数,那么结果一定非负,因为假如负数的个数有偶数个,那么我们成对选它,假如是奇数个,我们就把某一个负数选出,再成对选即可。
若k是奇数,那么所有数均负,那么答案《0,如果至少存在一个非负数,那我们先选一个非负数,然后问题就转化成了上一个形式。
因此我们排一下序,假如k是偶的,那么我们从两端成对的选,k是奇数,那么一定先选正的(若选负的那么后面也是选奇数个,这样就没有区别了),接下来就是刚才的问题了。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=100010,mod=1e9+9;
typedef long long LL;
int n,k;
int a[N];
int main(){cin>>n>>k;for(int i=0;i<n;i++) scanf("%d",&a[i]);sort(a,a+n);int res=1;int l=0,r=n-1;int sign=1;if(k%2){res=a[r--];k--;if(res<0) sign=-1;}while(k){LL x=(LL)a[l]*a[l+1],y=(LL)a[r-1]*a[r];if(x*sign>y*sign){res=x%mod*res%mod;l+=2;}else{res=y%mod*res%mod;r-=2;}k-=2;}cout<<res;
}接题:

首先,后缀表达式也可以实现括号操作,首先假如没有负号,那么都是直接相加。
同时我们可以把减号从M变成1(1-(a-b-c---)),最多有N+M个减号。
因此我们减一个最小值,同时必须加最大值(第一个一定是正的),其他加绝对即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=200010;
int n,a[N],m;
int main(){cin>>n>>m;int k=n+m+1;for(int i=0;i<k;i++) scanf("%d",&a[i]);if(m==0){LL res=0;for(int i=0;i<k;i++) res+=a[i];cout<<res;return 0;}sort(a,a+k);LL res=a[k-1]-a[0];for(int i=1;i<k-1;i++) res+=abs(a[i]);cout<<res;
}接题:

我们不妨看看前缀和,我们会惊奇的发现,我们每一次操作相当于交换一下他和它前面的前缀和,因此问题就转化成了求最大前缀和差值的min,并且两端是固定的,中间一段可以任意交换。
那么怎么求?我们不妨假设a[0]<a[n],同时确定其中的max与min。

此时,我们把图像向y轴投影压缩成一条线段,然后排一下序得到:
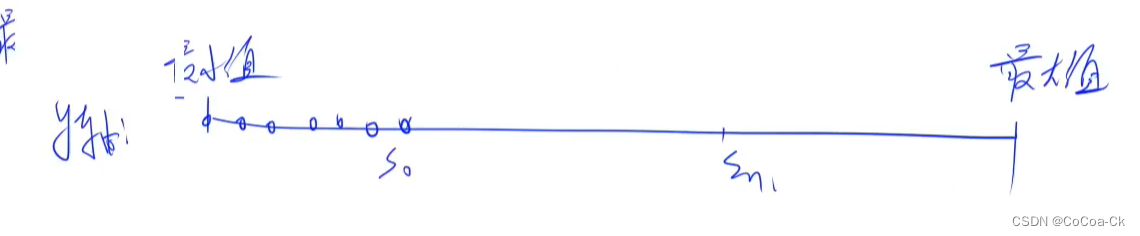
那么怎么走最优?
显然我们从S0开始向左两点走一步,即跨一个点走一步是最优的。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=300010;
LL a[N],s[N];
bool st[N];
int n;
int main(){int t;cin>>t;while(t--){scanf("%d",&n);s[0]=0;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);s[i]=s[i-1]+a[i];}LL s0=s[0],sn=s[n];if(s0>sn) swap(s0,sn);sort(s,s+n+1);//注意起点在0上for(int i=0;i<=n;i++){if(s[i]==s0){s0=i;break;}}for(int i=0;i<=n;i++){if(s[i]==sn){sn=i;break;}}memset(st,0,sizeof(st));int l=0,r=n;for(int i=s0;i>=0;i-=2){a[l++]=s[i];st[i]=1;}for(int i=sn;i<=n;i+=2){a[r--]=s[i];st[i]=1;}for(int i=0;i<=n;i++){if(st[i]==0) a[l++]=s[i];}LL res=0;for(int i=1;i<=n;i++){res=max(res,abs(a[i]-a[i-1]));}cout<<res<<endl;}
}









 懒汉单例模式)


时间序列)



题解 pb_ds 模版)

