1.引入—多项式表示
对于多项式,如何使用程序进行编写呢?
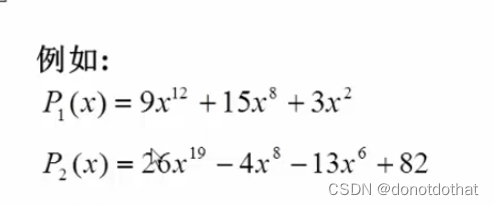
方法一:一维数组。下标对应未知数的指数,元素个体对应系数。缺点就是都得全部表示,系数为0项的存在浪费空间。例如,x只有一次方和2000次方,那么必须建立一个a[2001]这样大的数组才能进行多项式的编写。
方法二:二维数组。一维数组中存在一维数组{{1,5},{4,8},{5,3}},这样保证了系数为0的项不占用空间,根本不用写入二维数组中去。
方法三:链表。链表中的data部分包括x的指数以及所对应的系数,最后由link部分链接到下一指数。
如何进行多项式之间的运算呢?
比如两多项式F1 和 F2之间进行加法运算,首先将两个多项式按照指数递减进行排序。从F1的第一项开始,开始和F2的第一项进行比较。指数大的先输出,指数小的继续和另一多项式的下一项进行比较。如果指数相等,那么系数相加再输出。
2.线性表的顺序储存

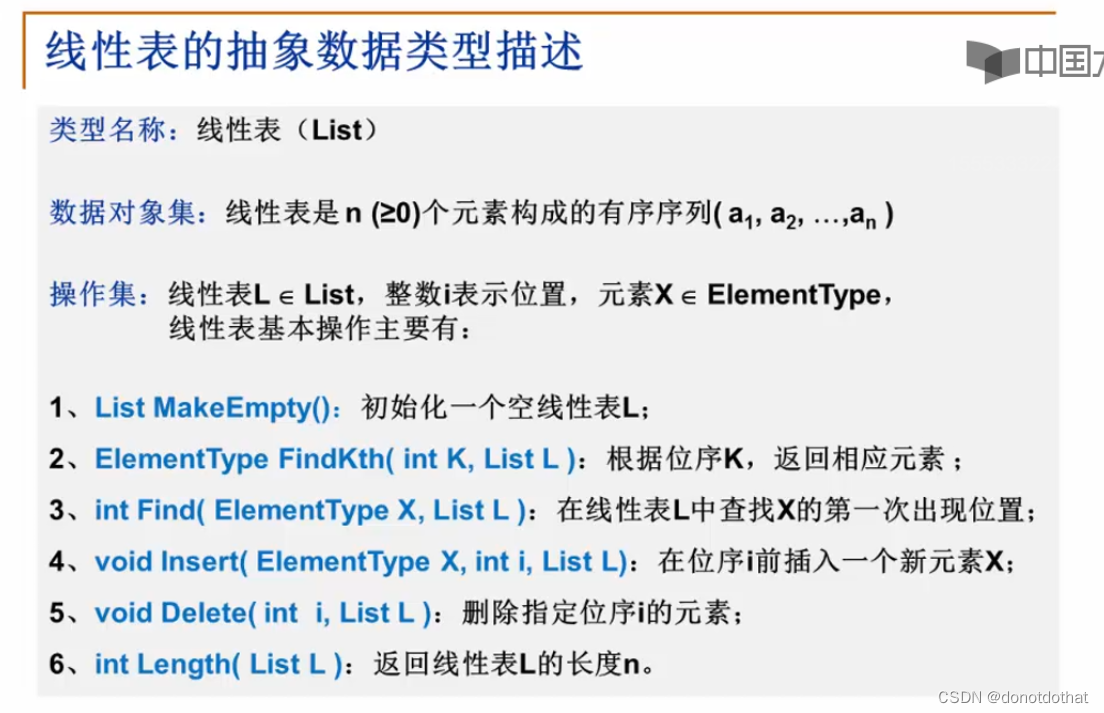
创建结构
#include <stdio.h>
#include <stdlib.h>
struct LNode{int Data[maxsize];//数据类型随便int last;//表示的是做后一个元素的下标
};
typedef struct LNode* List;
struct LNode L;
List PtrL;
//访问下标为i的元素:
L.Data[i];/ PtrL->Data[i];
//线性表的长度:
L.last + 1 / PtrL->last +1
初始化—建立空的线性表
List MakeEmpty()
{List PtrL;//表明Ptrl是指向结构类型的指针L = (List)malloc(sizeof(struct LNode));//分配内存用于储存数据。L->last = -1;//若数组中存在一个元素,这个元素的下标就是0,last = 0;若线性表为空,表示数组中没有元素,那么last = -1.
}
查找
int Find(int X,List PtrL)//传入要查找的元素(注意数据类型要和数组的一致)和指向线性表结构的指针,因为使用循环会用到数组的大小
{int result = -1;for(int i = 0,i < (PtrL->last + 1/*数组的长度*/),i++){if(PtrL->Data[i] == X){result = i;break;}}return result;
}
插入
想要实现在数组Data[]的第i个位置上插入元素X,即对应的下标为Data[i-1]。那么首先要做的事情就是将第i个位置及其之后的元素全部向后挪动一位,再进行插入的操作。
void Insert(int i/*要插入的位置*/,int X/*要插入的元素*/,List PtrL)
{if(PtrL->last + 1 == maxsize)printf("不好意思,表已经满了,不可进行插入操作");else if(i <= 0 || i>=maxsize)printf("请输入有效的位置!");for(int j = Ptrl->last;j>= i-1;j--){PtrL->Data[j+1] = PtrL->Data[j];//注意要 从后向前 逐次后退一格}PtrL->Data[i-1] = X;//下标为i-1的就是第i个元素PtrL->last++;//因为实现了元素的插入,最后一个元素下标要+1
}
如果表没有满,那么我们不确定到底空出了几个位置,但是PtrL->last告诉了我们最后一个元素的准确位置,直接使用last即可,即从最后一个元素开始向后挪动。
删除
对数组中第i个位置元素进行删除,那么之后数组中第i个位置就空出来了,之后需要对i之后的所有元素进行向前挪动一位。
void Delete(int i;List PtrL)
{if(i <= 0 || i > PtrL->last+1)printf("请输入有效的位置!");for(int j = i-1/*第i个元素要被填上*/;j <= PtrL->last;j++){PtrL->Data[j] = PtrL->Data[j+1];//注意从前向后依次向前挪动}PtrL->last--;
}
2.线性表的链式储存
使用顺序储存的时候,因为数组中的元素在内存中是连续的,所以每当对线性表进行操作的时候,往往会进元素的挪动。而使用链结构,只要轻易地修改链就行了,不需要对元素进行挪动。
--------关于指向结构类型的指针P的理解:P指向了一个结构体,里面包含data部分和Next部分,P = P->Next就实现了指针之间的赋值,其实P还是指针。那么就可以将P理解为一个结构体?P既指向了data部分又指向了Next部分。
创建结构
typedef struct LNode* List;
struct LNode{int data;List Next;
};
List PrtL = malloc(sizeof(struct LNode));
求表长
int Length(List PtrL/*传入的是表头*/)
{int count = 0 ;List p = PrtL;while(p->Next != NULL){count++;p = p->Next;}return count++;
}
查找
寻找data=X的结点的位置:
int Find(int X,List PtrL)
{List P = PtrL;int locate = 1;while(P->data != X && P->Next != NULL)//条件对应两种情况。如果最后P->data=X,那么无论P此时是不是表尾,都要返回locate;else就是找遍了链表就是没找到。{P= P->Next;locate++;}int result = -1;if(P->data == X){result = locate;}return locate;
}
寻找第K个节点
List FindKth(int K;List PtrL)
{List P = PtrL;int order = 1;while(P->Next != NULL){P = P->Next;order++:if(order == K )break;}return P;
}
插入
在第i-1的节点后面(也就是第i个节点)插入一个值为X的新节点。
——关于什么时候需要用malloc函数申请空间的思考:
当我们需要构造一个全新节点的时候,需要申请空间;但是当仅仅是使用新指针变量指向一个已经存在的节点的时候,不需要重新申请空间。因为两个指针变量指向了同一个结点,无需开辟新的空间。
void Insert(int X,int i,List PtrL)
{//创建一个新节点List new = malloc(sizeof(struct LNode));new->data = X;//代码的健壮性if(i == 1)//特殊位置:表头{new->Next = PtrL;//这样链表头就发生了改变,要调用new作为表头}else if(i == length(PtrL)+1)//特殊位置:表尾(也就是说直接在表尾增加一个新的节点){FindKth(length(PtrL))->next = new;new->Next = NULL;}else if(i>length(PtrL))//检查是否合法{printf("无法插入");}else//一般位置{new->Next = FindKth(i;PtrL);//原来的第i个节点将会变成第i+1个FindKth(i-1;PtrL)->Next = new;//原来的第i-1个节点就指向了new}
}
也可以改变函数的返回类型,返回插入完成的链表头,这样就可以方便进行赋值操作PtrL = Insert(int X,int i,List PtrL);注意如果链表头变成了新创建的指针new,那么原来的PtrL就相当于指向了链表的第二个结点。一般情况下函数返回头指针赋值给PtrL,保持PtrL作为头指针不变。
删除
删除链表中的第i个节点,就将第i-1个节点直接指向第i+1个节点,跳过第i个节点,完成连接。注意删掉的结点i是要释放空间的。
List Delete(int i,List PtrL)
{List s;//先考虑一头一尾if(i == 1)//删除的是头结点{if(PtrL != NULL)//考虑链表是否是空的{s = FindKth(i,PtrL);free(s);PtrL = PtrL->Next;}else printf("整个链表是空链表,没法再删了");}else if(i = length(PtrL)){s = FindKth(i,PtrL);free(s);FindKth(i-1,PtrL)->Next = NULL;}else if(i<=0 || i>length(PtrL))//检查合法性{printf("请输入合法的位置!");}else//一般情况{s = FindKth(i,PtrL);free(s);FindKth(i-1,PtrL)->Next = FindKth(i+1,PtrL); }return Ptrl;
}
3.广义表和多重链表
广义表
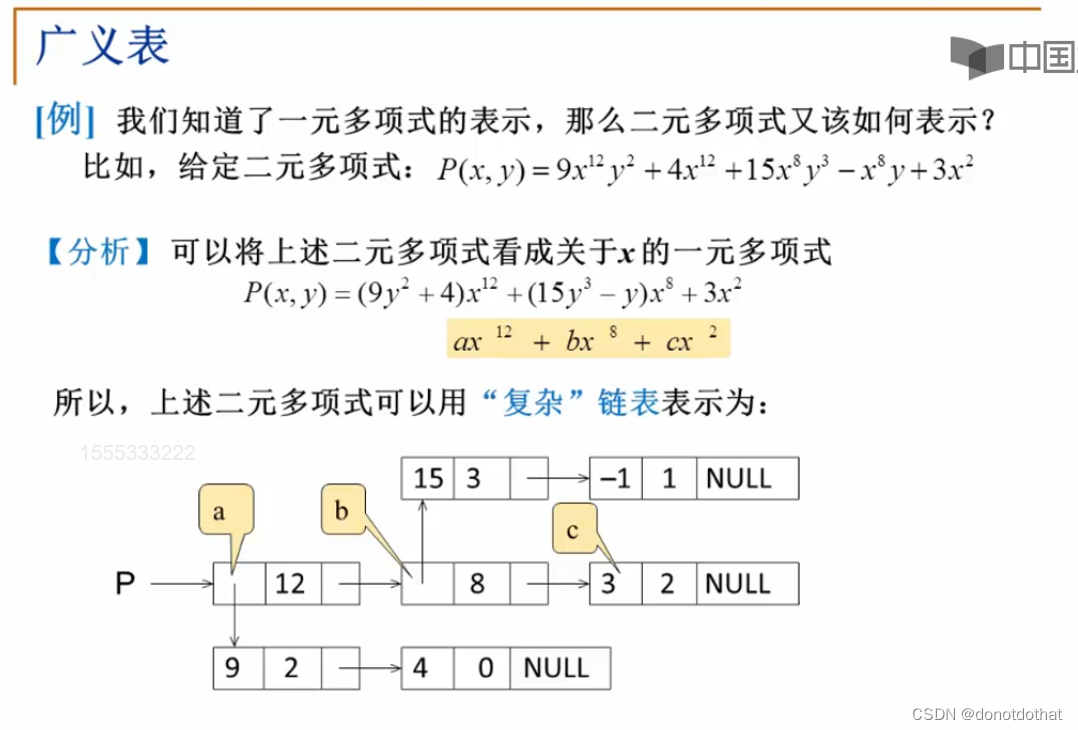
将二元多项式整理成一元多项式,使用链表。
数据部分:系数(一元多项式)、指数次方;link部分指向下一个节点。
也就是说,在关于x的一元多项式里面嵌套了关于y的一元多项式。原来线性表的系数部分是常量,只不过现在变成了有关y的一元多项式。

广义表就属于多重链表

多重链表中的节点可能属于多个链,也就是说它里面会有多个指针域,分别指向不同链中的下个节点。
eg.矩阵

稀疏矩阵就是0项非常多,使用数组就会造成大量的空间储存的是0,空间浪费严重。

十字链表来实现稀疏矩阵
data部分:行坐标i、列坐标j、元素的值A(i,j);
指针域LInk部分:行指针Right、列指针Down,是指向同一行中下一个节点和同一列中下一个节点的指针。
也就是说每个节点都需要与他最近的列和行的元素连接起来。每个节点同时属于他所在的行和他所在列。
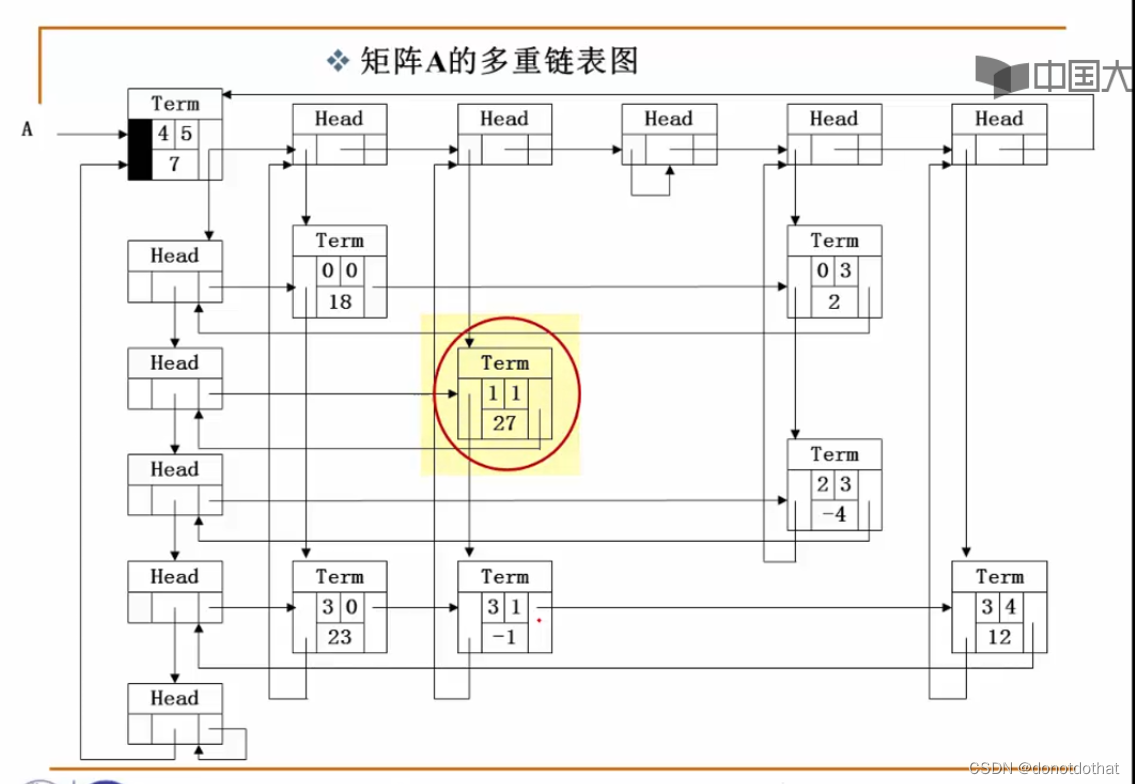
- 这里有两种类型的节点。
一种是Term类型代表矩阵中的非零项,data表示的是行、列、数值,它具有两个指针(行、列),同一行同一列都设计成循环链表。
另一种是Head节点,不同的Head作为了行链表的头结点、列链表的头结点。
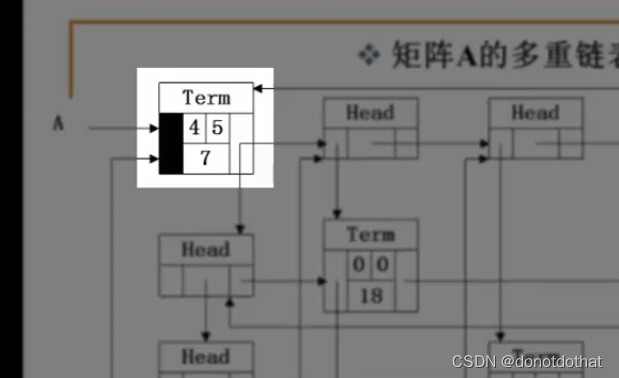
- 左上角的Term节点比较特殊,他是整个矩阵的入口,他的行值、列值、数值4,5,7,表示这个矩阵有4行5列,非零项个数有7个。他也具有两个指针,通过这两个指针就可以找到所有列的头结点和所有行的头结点。他就是整个矩阵的说明信息。
#include <stdio.h>
#include <stdlib.h>// 定义稀疏矩阵的节点结构体
typedef struct Node {int row, col, value;struct Node* right;struct Node* down;
} Node;// 创建新节点的函数
Node* createNode(int row, int col, int value) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->row = row;newNode->col = col;newNode->value = value;newNode->right = NULL;newNode->down = NULL;return newNode;
}// 定义稀疏矩阵结构体
typedef struct SparseMatrix {int rows, cols;Node* head; // 头指针
} SparseMatrix;// 创建稀疏矩阵的函数
SparseMatrix createSparseMatrix(int m, int n) {SparseMatrix matrix;matrix.rows = m;matrix.cols = n;// 创建头指针节点,表示头结点matrix.head = createNode(-1, -1, 0);matrix.head->right = matrix.head; // 将右指针和下指针指向自身,构成一个环形链表matrix.head->down = matrix.head;return matrix;
}// 向稀疏矩阵插入元素的函数
void insert(SparseMatrix* matrix, int row, int col, int value) {Node* newNode = createNode(row, col, value);Node* currentRow = matrix->head;while (currentRow->down != matrix->head && currentRow->down->row < row) {currentRow = currentRow->down;}Node* currentColumn = currentRow;while (currentColumn->right != currentRow && currentColumn->right->col < col) {currentColumn = currentColumn->right;}newNode->right = currentColumn->right;currentColumn->right = newNode;currentColumn = matrix->head;while (currentColumn->right != matrix->head && currentColumn->right->col < col) {currentColumn = currentColumn->right;}newNode->down = currentColumn->right;currentColumn->right = newNode;
}int main() {SparseMatrix matrix = createSparseMatrix(3, 3); // 创建一个3x3的稀疏矩阵insert(&matrix, 0, 2, 5); // 向矩阵中插入元素insert(&matrix, 1, 1, 3);insert(&matrix, 2, 0, 4);return 0;
}
在调用指针之前一定要保证指针的内容是存在的而不是NULL
while(p && p->data != e)//当p存在并且...
{
}


)




图论)





-- 用launch命令管理启动项)

)



