前言:
在前面我们已经学习了数据结构的基础操作:顺序表和链表及其相关内容,今天我们来学一点有些难度的知识——数据结构中的二叉树,今天我们先来学习二叉树中堆的知识,这部分内容还是非常有意思的,下面我们就开始慢慢学习
准备工作:本人习惯将文件放在test.c、SeqList.c、SeqList.h三个文件中来实现,其中test.c用来放主函数,SeqList.c用来放调用的函数,SeqList.h用来放头文件和函数声明
一、什么是树
在正式进行二叉树的学习之前,我们要了解一下树是何物,其实我们经常讲到的计算机中的树其实是以数组的形式存在在内存中的,只是它的可以形象化成树的形状,如下:
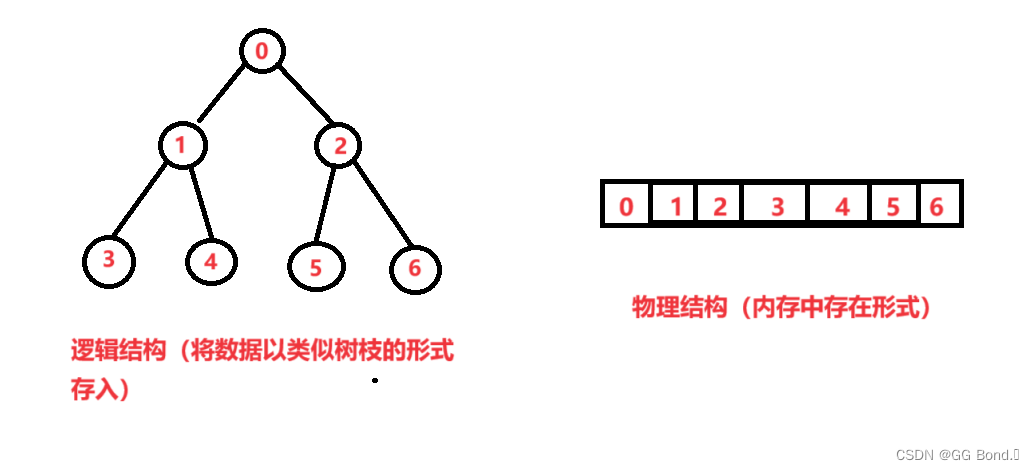
如图,其中0所在位置被称为树顶或者树根都可以,下面的称为子树,其中1所在分叉称为左子树,2所在分叉成为右子树
还有一些规则如下:

对于学过离散数学的同学来说这部分知识并不难,没有学过的自己再去搜一下了解一下吧,这里只讲了一些大概内容
二、什么是堆
树里面有几个特殊的概念,例如完全二叉树和满二叉树,而堆就是完全二叉树的一种,完全二叉树就是除了最后一层外,其他层节点数达到最大
堆与普通的完全二叉树的不同在于它的大小堆的性质
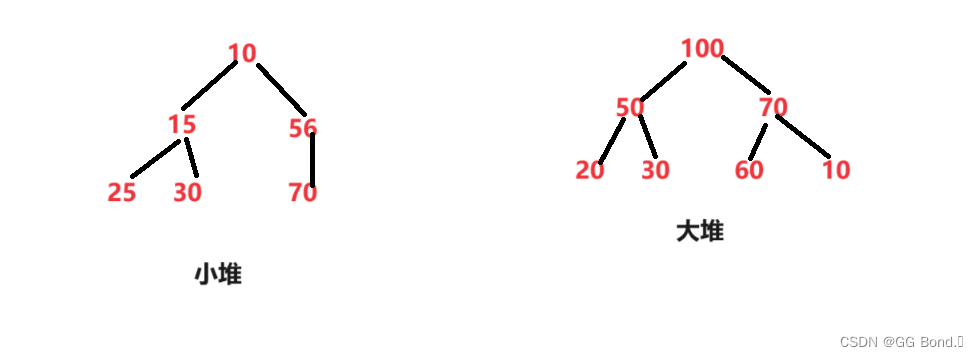
大堆:树任何一个父亲>=孩子
小堆:树任何一个父亲<=孩子
例如:
三、堆的节点结构
堆用的顺序表的结构,所以堆的节点结构与顺序表差异不大
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;
堆的节点结构很简单,定义一个指针,两个表示容量的整形即可
四、堆的基本操作
//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);看上面的函数声明部分我们就可以看到我们每一步要实现的内容,接下来,我们就来一步一步进行实现
1、初始化
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
2、销毁
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
3、插入元素
插入元素时要先检查空间是否够用,如果不够用要先进行扩容
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
在这一步我们还创建了几个其他的函数分担一些功能,这些函数在后文中也有应用
4、判断栈顶元素是否为空
这一步在下面有用到,例如当删除树根元素时,如果树根元素为空就无法操作,所以需要判断树根元素是否为空
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
5、删除元素
这里删除元素是删除树根元素
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
6、返回树根元素
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
7、算个数
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
}五、完整代码实例
SeqList.h
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);test.c
//堆
int main()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d ", top);HeapPop(&hp);}return 0;
}SeqList.c
//堆
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
}



)
Jedis客户端、SpringDataRedis客户端)

、kibana、libreoffice)


)


:adc adc128s102)

)

—Dubbo服务引用源码(1))
)
