接前一篇文章:软考 系统架构设计师系列知识点之云原生架构设计理论与实践(7)
所属章节:
第14章. 云原生架构设计理论与实践
第2节 云原生架构内涵
14.2 云原生架构内涵
关于云原生的定义有众多版本,对于云原生架构的理解也不尽相同。本节将根据广泛的云原生技术、产品和上云实践,给出一般性的理解。
14.2.3 主要架构模式
云原生架构有非常多的架构模式,这里选取一些对应用收益更大的主要架构模式进行讨论。
1. 服务化架构模式
2. Mesh化架构模式
3. Serverless模式
Serverless将“部署”这个动作从运维中“收走”,使开发者不用关心应用运行地点、操作系统、网络配置、CPU性能等。从架构抽象上看,当业务流量到来/业务事件发生时,云会启动或调度一个已启动的业务进程进行处理,处理完成后,云会自动关闭/调度业务进程,等待下一次触发,也就是把应用的整个运行都委托给云。
Serveless并非适用任何类型的应用,因此架构决策者需要关心应用类型是否适合于Serverless运算。如果应用是有状态的,由于Serverless的调度不会帮助应用做状态同步,因此云在进行调度时可能导致上下文丢失;如果应用是长时间后台运行的密集型计算任务,会无法发挥Serverless的优势;如果应用涉及频繁的外部I/O(网络或者存储,以及服务间调用),会因为繁重的I/O负担、时延大而不合适。事件驱动架构图如图14-2所示:
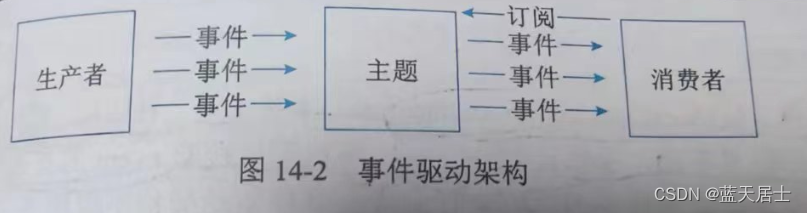
Serverless非常适合于事件驱动的数据计算任务、计算时间短的请求/响应应用、没有复杂相互调用的长周期任务。
4. 存储计算分离模式
分布式环境中的CAP困难主要是针对有状态应用,因为无状态应用不存在C(一致性)这各维度,因此可以获得很好的A(可用性)和P(分区容错性),因而获得更好的弹性。在云环境中,推荐把各类暂态数据(如session)、结构化和非结构化持久数据都采用云服务来保存,从而实现存储计算分离。但仍然有一些状态如果保存到远端缓存,会造成交易性能的明显下降,比如交易会话数据太大、需要不断根据上下文重新获取等,这时可以考虑通过采用时间日志+快照(或检查点)的方式,实现重启后快速增量恢复服务,减少不可用对业务的影响时长。
5. 分布式事务模式
微服务模式提倡每个服务使用私有的数据源,而不是像单体这样共享数据源。但往往大颗粒度的业务需要访问多个微服务,必然带来分布式事务问题,否则数据就会出现不一致。架构师需要根据不同的场景,选择合适的分布式事务模式。
(1)传统采用XA模式,虽然具备很强的一致性,但是性能差。
(2)基于消息的最终一致性(BASE)通常有很高的性能,但是通用性有限。
(3)TCC模式完全由应用层来控制事务,事务隔离性可控,也可以做到比较高效;但是对业务的侵入性非常强,设计开发维护等成本很高。
(4)SAGA模式与TCC模式的优缺点类似,但没有try这个阶段,而是每个正向事务都对应一个补偿事务,也是开发维护成本高。
(5)开源项目SEATA的AT模式非常高性能且无代码开发工作量,且可以自动执行回滚操作,同时也存在一些使用场景限制。
更多内容请看下回。





)
)












)