C++ 二叉树OJ题

💓博主CSDN主页:麻辣韭菜-CSDN博客💓

⏩专栏分类：C++知识分享⏪

🚚代码仓库:C++高阶🚚

🌹关注我🫵带你学习更多C++知识
🔝🔝

前言

C++二叉搜索树这篇讲解了搜索二叉树的实现的，本篇从实战出发，让大家更好的掌握和理解二叉树的！！！！

1. 二叉树创建字符串。606. 根据二叉树创建字符串 - 力扣（LeetCode）

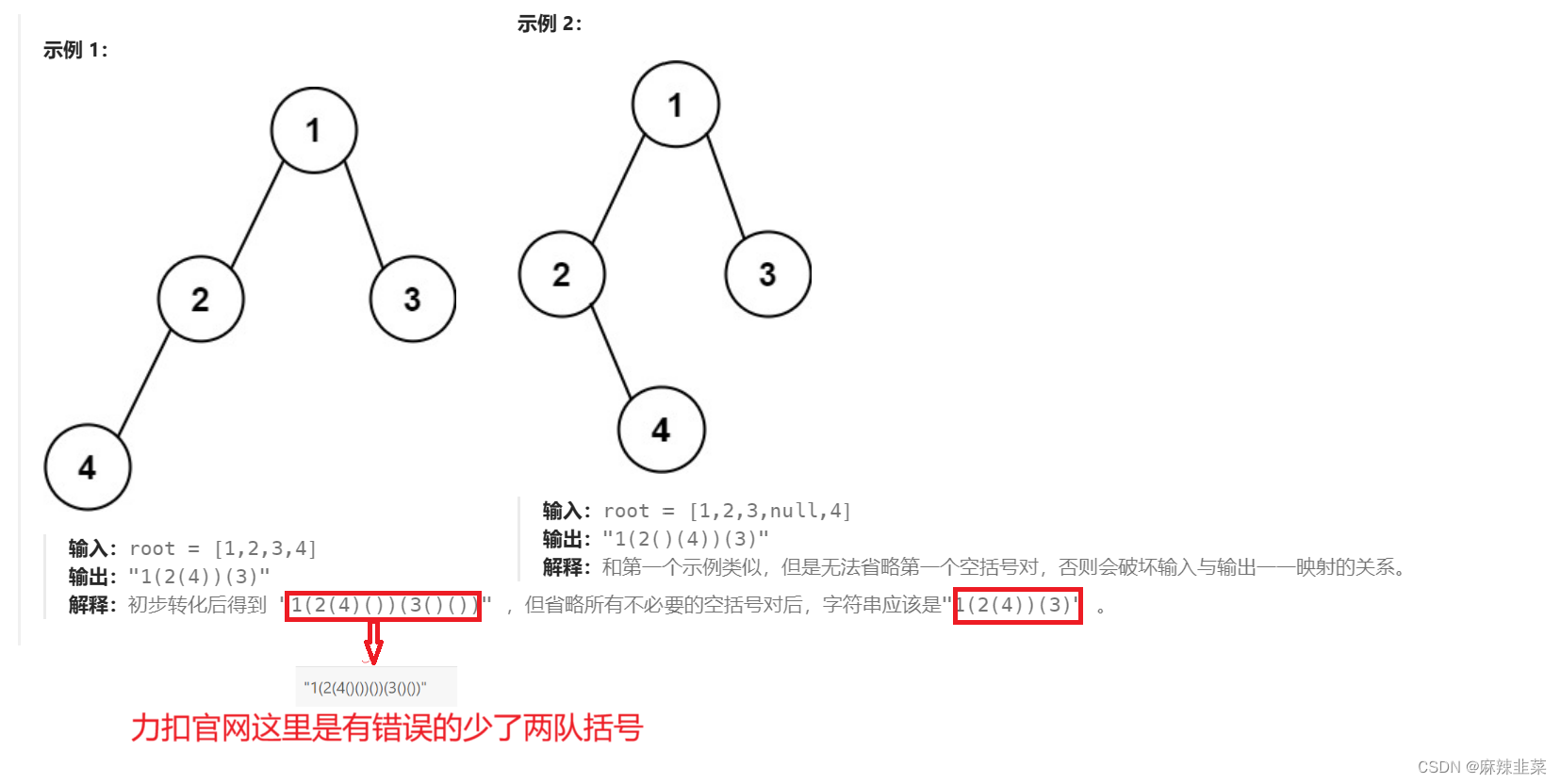
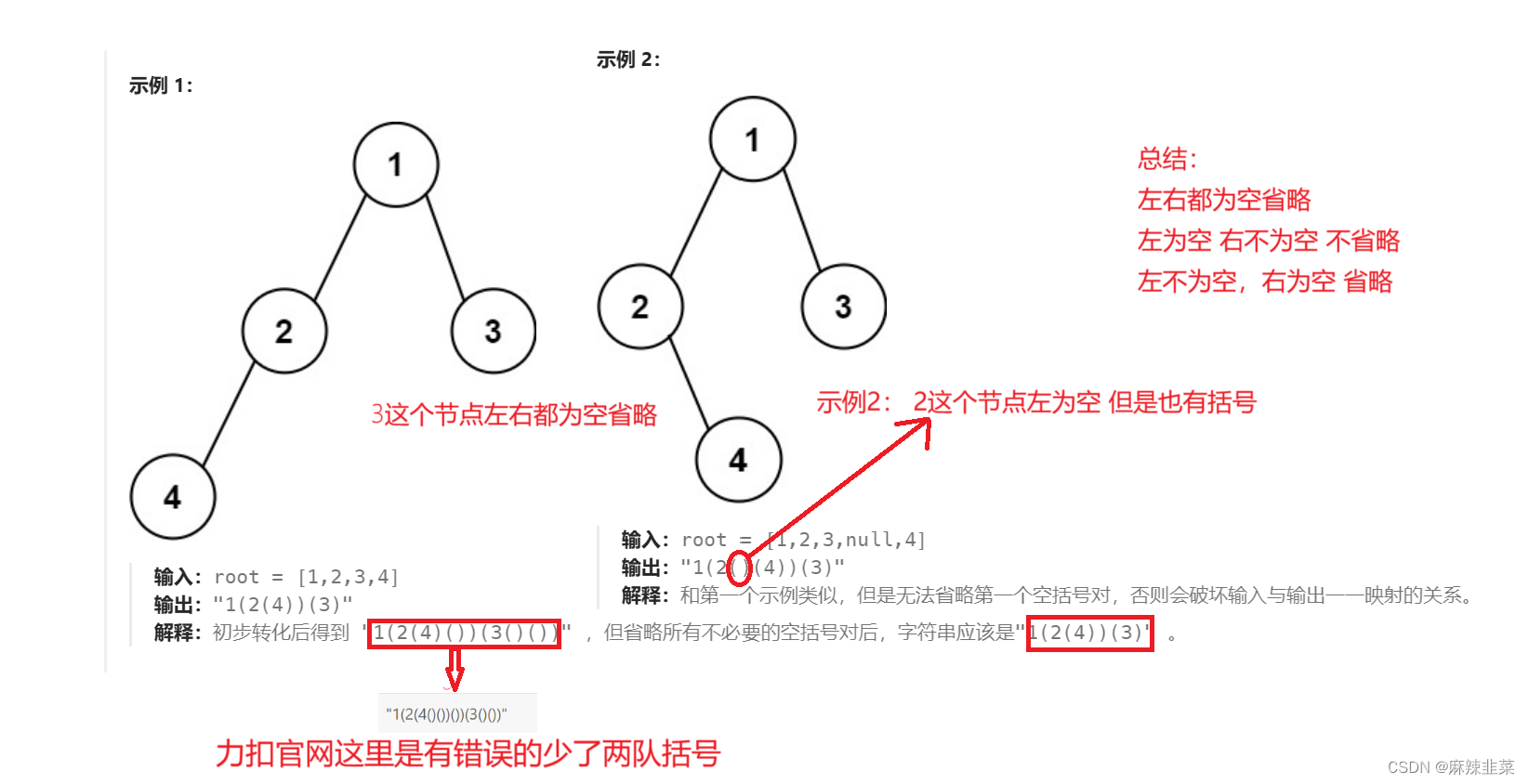
找出规律，我们就好办了直接代码演示。

class Solution {
public:string tree2str(TreeNode* root) {if(root == nullptr) //根为空 直接返回空串！return "";string str  = to_string(root->val); //外面解释这个函数//结合 刚才的3点总结 左右都为空不加括号，左为空是要加括号的。 if(root->left || root->right){str += '(';str += tree2str(root->left);str += ')';}if(root->right){str += '(';str += tree2str(root->right);str += ')';}return str;}
};

to_string 是 C++ 标准库中的一个函数，它定义在 <string> 头文件中。这个函数用于将一个数值类型（如 int、double 等）转换为其对应的字符串表示形式。在给出的代码片段中，to_string(root->val) 被用来将 TreeNode 对象的 val 属性（假设是一个数值类型）转换为一个字符串。这样，就可以将该字符串与其他部分拼接起来，形成最终的树形结构字符串表示。例如，如果 root->val 是整数 3，那么 to_string(root->val) 将返回字符串 "3"。简而言之，to_string 函数在 C++ 中用于数值到字符串的转换。在你的代码中，它被用来将树节点的值转换为字符串，以便构建树结构的字符串表示。

这里有点难理解是左不为空，右为空。按照上面条件不是就错了吗？

我们按照题的要求前序遍历，是先根在左然后右看递归展开图

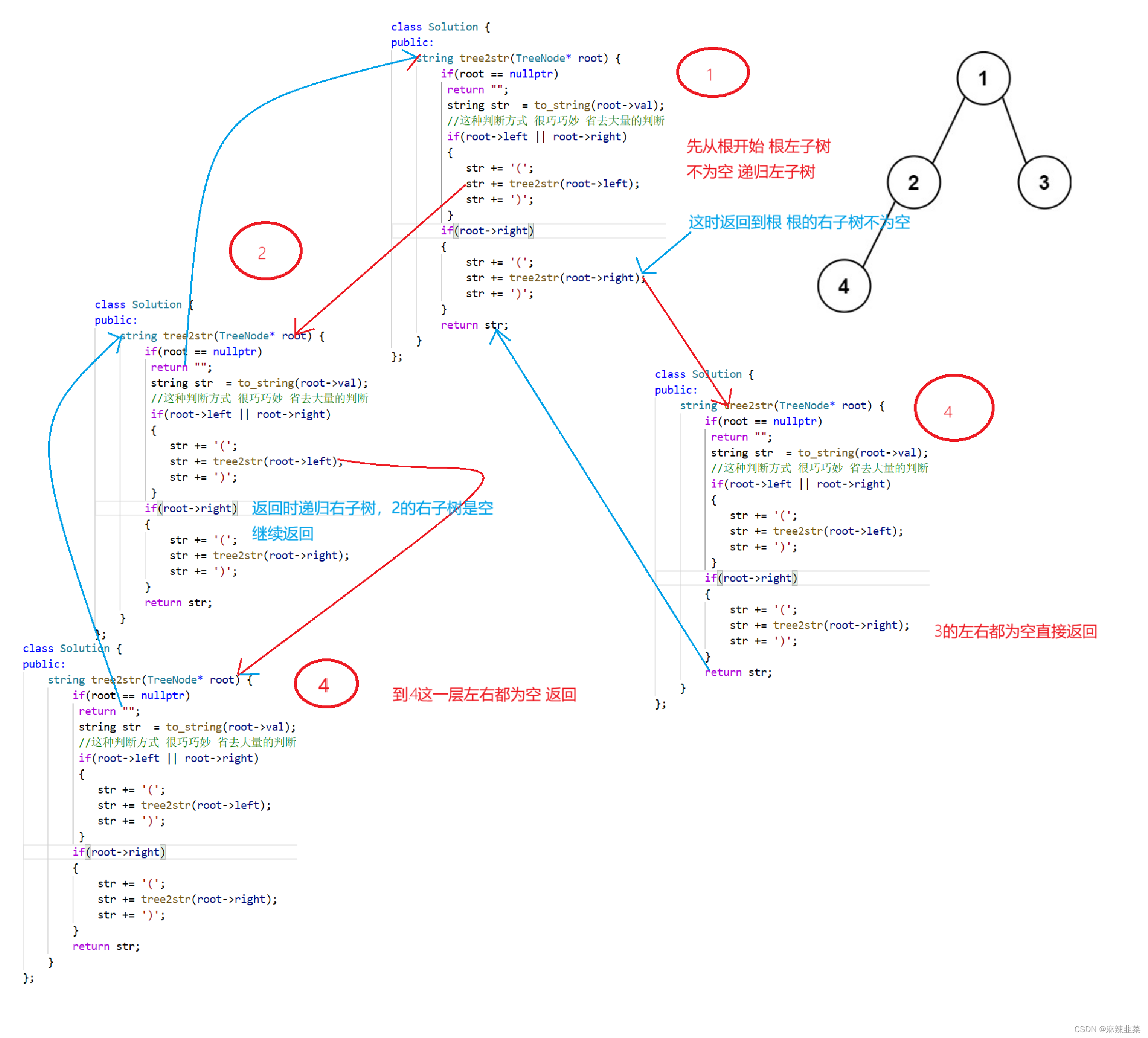
递归是一层一层展开，如果左不为空，右为空它们就会像上图那样一直找到左为空为止，

这时在递归右子树。

2. 二叉树的分层遍历1。102. 二叉树的层序遍历 - 力扣（LeetCode）

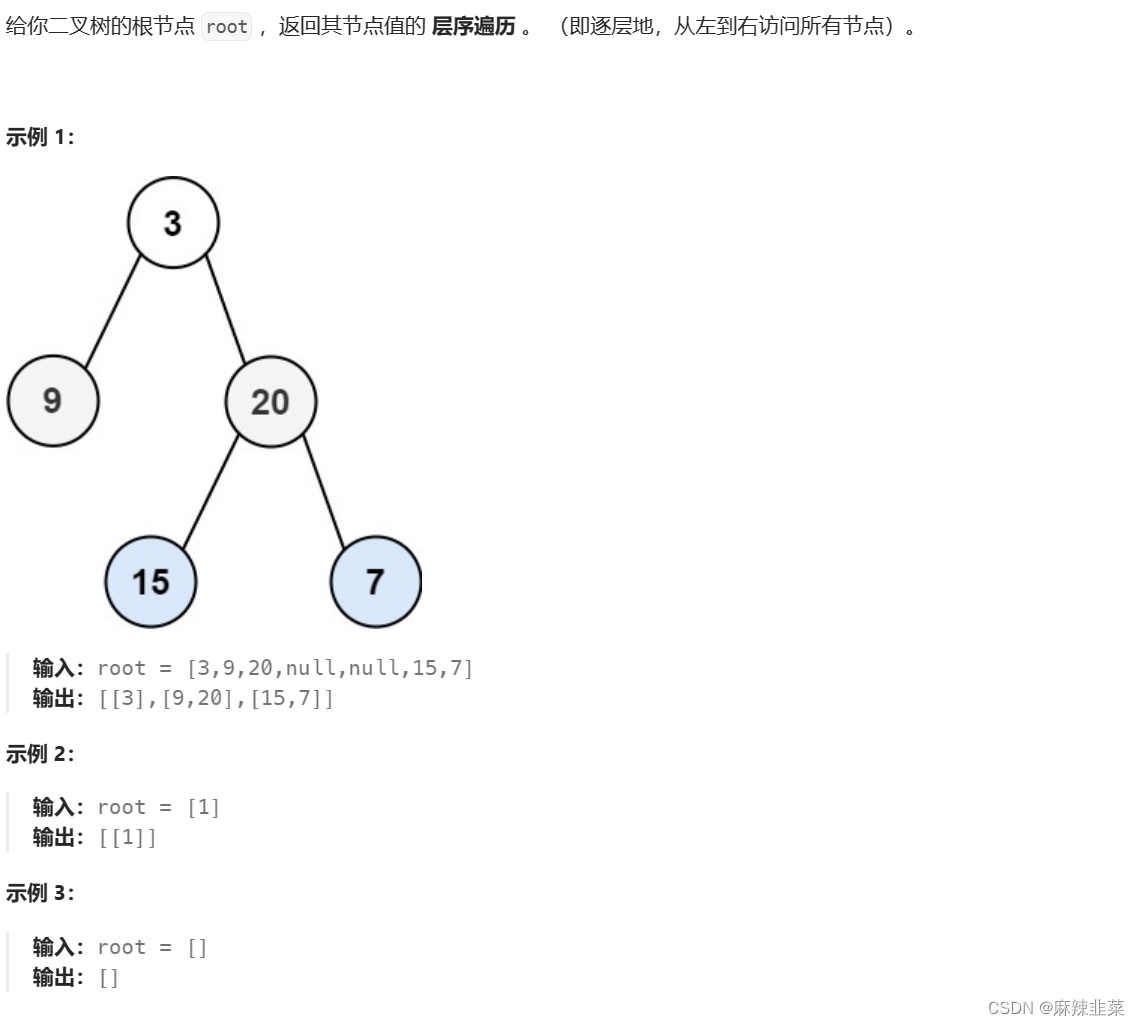
解题思路：我们创建一个队列，前序遍历这个数组，每遍历一次，就进队列一次，

根据队列的性质先进先出。就解决了！！！

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode* > q; //创建队列int levelSize = 0; //层数变量vector<vector<int>> vv;if(root) //节点不为空进队列{q.push(root);levelSize = 1; //为什么是1 根就只有一个。}while(!q.empty()) //如果队列不为空{vector<int> v;while(levelSize){TreeNode* front = q.front();q.pop();//出队列v.push_back(front->val); //把队顶的数据压进顺序表V//带入下一层if(front->left)q.push(front->left);if(front->right)q.push(front->right);--levelSize;}vv.push_back(v); //把每一层出完，压进二维的顺序表levelSize = q.size();//更新每一层，数据有多少个。}return vv;}
};

3. 二叉树的分层遍历2。107. 二叉树的层序遍历 II - 力扣（LeetCode）

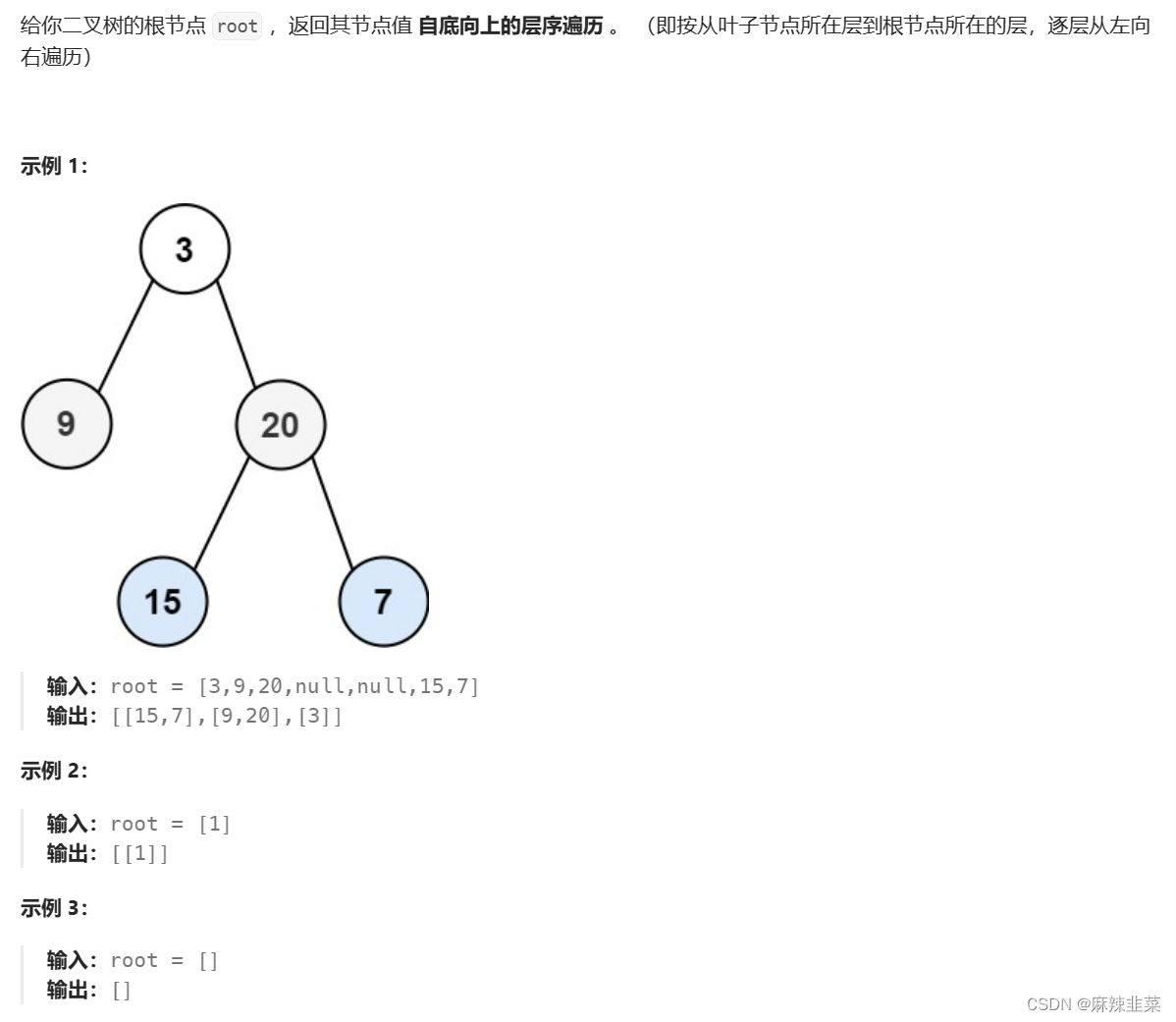
这个题没什么好说的，来个投机的，把第二题逆置再返回。

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode* > q; //创建队列int levelSize = 0; //层数变量vector<vector<int>> vv;if(root) //节点不为空进队列{q.push(root);levelSize = 1; //为什么是1 根就只有一个。}while(!q.empty()) //如果队列不为空{vector<int> v;while(levelSize){TreeNode* front = q.front();q.pop();//出队列v.push_back(front->val); //把队顶的数据压进顺序表V//带入下一层if(front->left)q.push(front->left);if(front->right)q.push(front->right);--levelSize;}vv.push_back(v); //把每一层出完，压进二维的顺序表levelSize = q.size();//更新每一层，数据有多少个。}reverse(vv.begin(),vv.end()); //用迭代器逆置return vv;}};

4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

解题思路根据解释，我们可以得出一个在我的左子树，一个在我的右子树。我就是公共祖先。那我们可以用路径相交思路来解决，比如7和0的公共祖先。根据递归深度路径大小，

让深度更深的那个先走，等它们深度一样时，同时再走，最后相等的那个值就是公共祖先。

class Solution {
public:bool GetPath(TreeNode* root,TreeNode* x,stack<TreeNode*>& path){if(root == nullptr) //根都为空了 还找个屁{return false;}//不为空进栈path.push(root);if(root == x) // 找到了{return true;}if(GetPath(root->left,x,path)) //左递归{return true;}if(GetPath(root->right,x,path))//右递归{return true;}path.pop();//刚才条件说 一个在我的右，一个在我的左，这里左右都为空了肯定不是祖先，出栈。return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> pPath,qPath; //这里用栈 先进后出GetPath(root,p,pPath);GetPath(root,q,qPath);while(qPath.size() != pPath.size()){if(qPath.size()>pPath.size())qPath.pop();elsepPath.pop();}while(qPath.top() != pPath.top()){qPath.pop();pPath.pop();}return qPath.top();}
};

5. 二叉树搜索树转换成排序双向链表。二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)

解题思路：中序遍历，然后改链接方向，如何改？根的左就是prev。右怎么改？记录父亲节点，根的右就是父亲节点以4举例：4的左为空，那它连接就是nullptr，再看右为空返回上一层这时父亲连接它的右

class Solution {
public:void InorderConvert(TreeNode* cur, TreeNode*& prev){if(cur == nullptr)return ;InorderConvert(cur->left,prev);cur->left = prev;if(prev)prev->right = cur;prev = cur;InorderConvert(cur->right,prev);}TreeNode* Convert(TreeNode* pRootOfTree){TreeNode* prev = nullptr;InorderConvert(pRootOfTree,prev);TreeNode* head = pRootOfTree;while (head && head->left) {head = head->left;}return head;}};

6. 根据一棵树的前序遍历与中序遍历构造二叉树。 105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

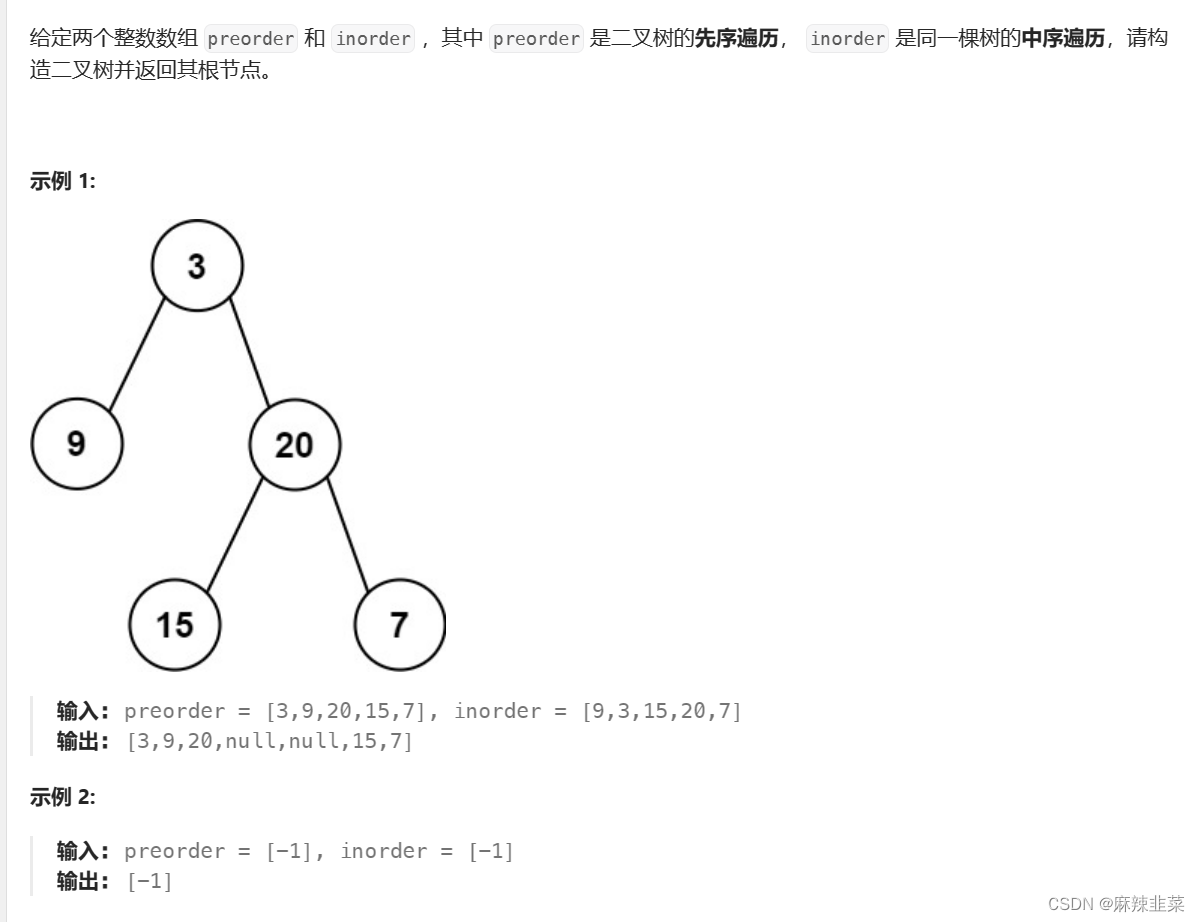
解题思路：前序确定什么？确定根，中序确定什么？确定根的左右区间

class Solution {
public:TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend){if(inbegin > inend){return nullptr;}TreeNode* root = new TreeNode(preorder[prei]);int rooti = inbegin;//分割区间while(rooti< inend){if(inorder[rooti] == preorder[prei]){break;}elserooti++;}++prei;// 区间[inbegin, rooti-1] prei [rooti+1,inend] //转化成子问题root->left = _buildTree(preorder,inorder,prei,inbegin,rooti-1);root->right = _buildTree(preorder,inorder,prei,rooti+1,inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i = 0;return _buildTree(preorder, inorder, i, 0, inorder.size()-1);}
};

7. 根据一棵树的中序遍历与后序遍历构造二叉树。106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

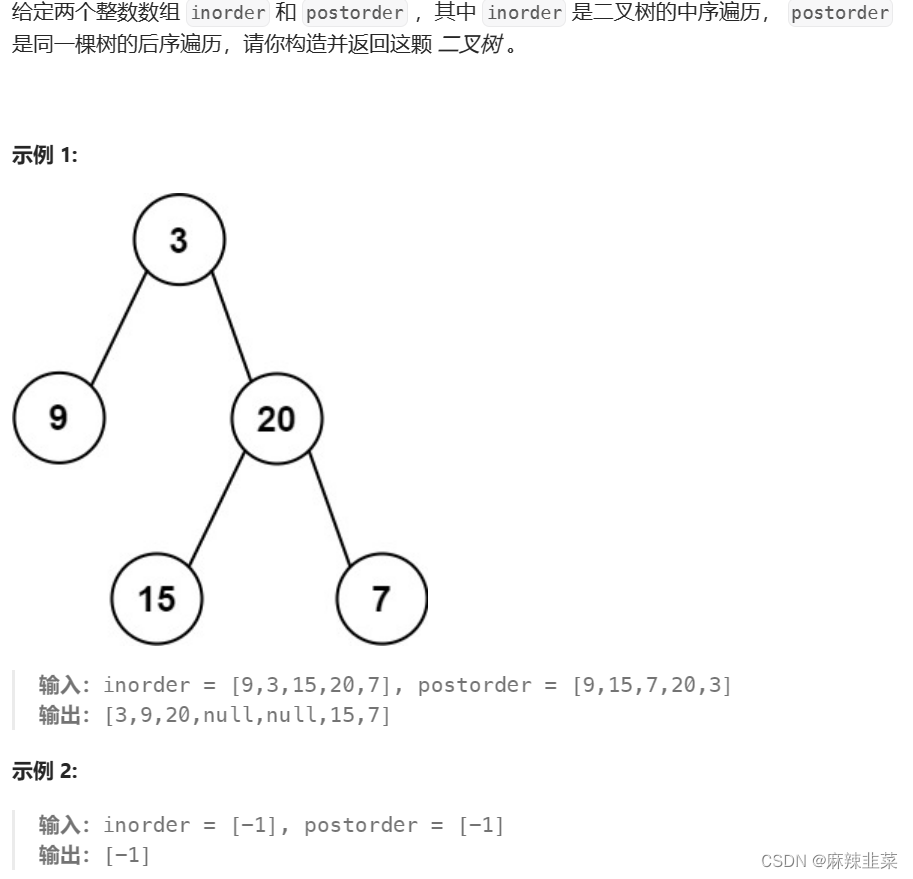
解题思路：还是一样，中序确定根的左右区间，后序确定根。先创建右再创建左


class Solution {
public:TreeNode*  _buildTree(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin, int inend){if(inbegin > inend){return nullptr;}TreeNode* root = new TreeNode(postorder[posti]);int rooti = inbegin;while(rooti < inend){if(inorder[rooti] == postorder[posti])break;else++rooti;}++posti;root->right= _buildTree(inorder, postorder,posti ,rooti+1, inend);root->left= _buildTree(inorder, postorder,posti ,inbegin, rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i = 0;reverse(postorder.begin(),postorder.end());return _buildTree(inorder, postorder,  i, 0, inorder.size()-1); }
};

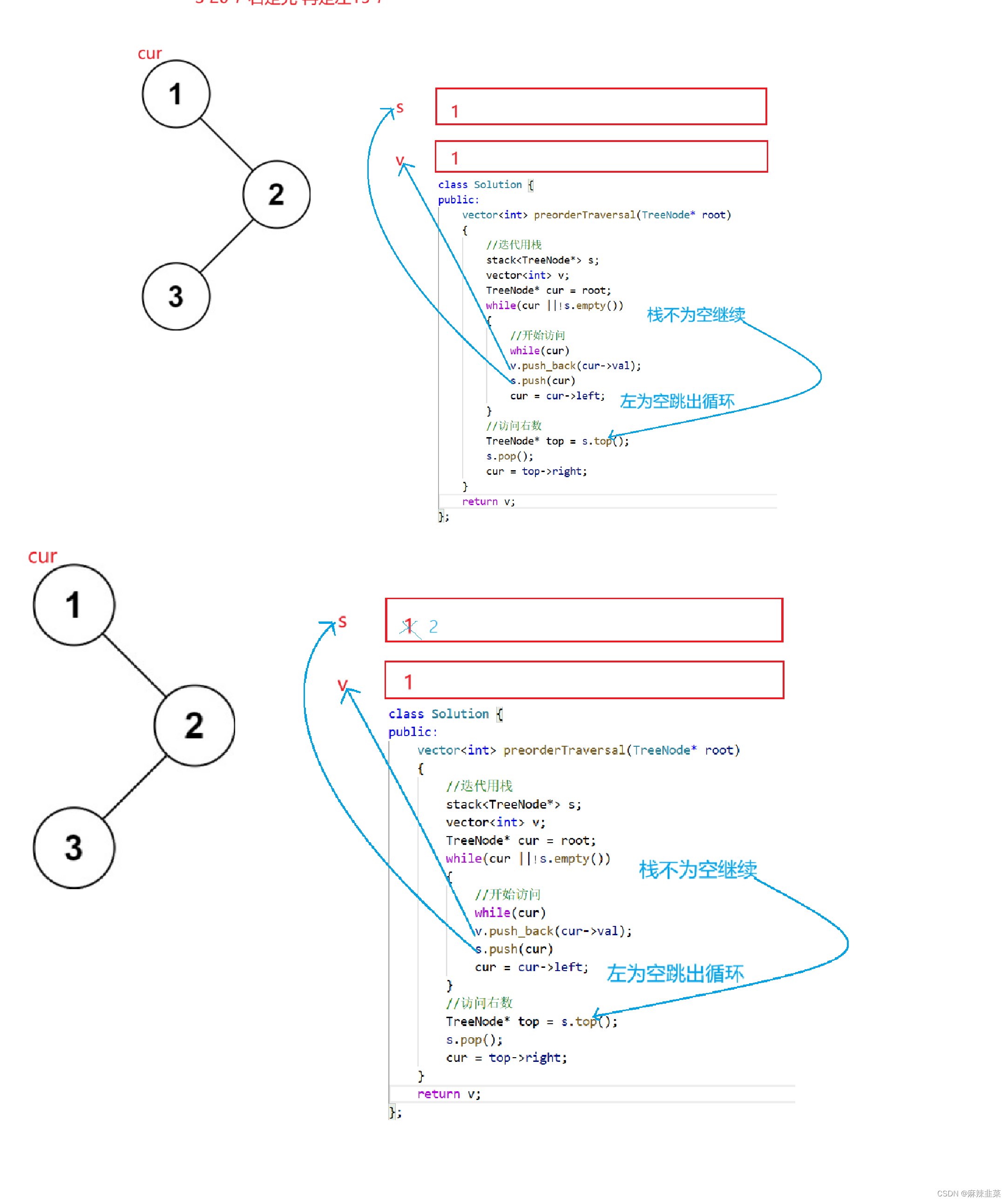
8. 二叉树的前序遍历，非递归迭代实现 144. 二叉树的前序遍历 - 力扣（LeetCode）。

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {//迭代用栈 stack<TreeNode*> s;vector<int> v;TreeNode* cur = root;while(cur || !s.empty()){//开始访问while(cur)v.push_back(cur->val);s.push(cur)cur = cur->left;}//访问右树TreeNode* top = s.top();s.pop();cur = top->right;}return v;
};

9. 二叉树中序遍历，非递归迭代实现。94. 二叉树的中序遍历 - 力扣（LeetCode）

解题思路：和前序不同的是先访问左再访问根然后右。那这样的话一直迭代到左树为空为止，然后取栈中取元素 push到vector中，最后访问右树。

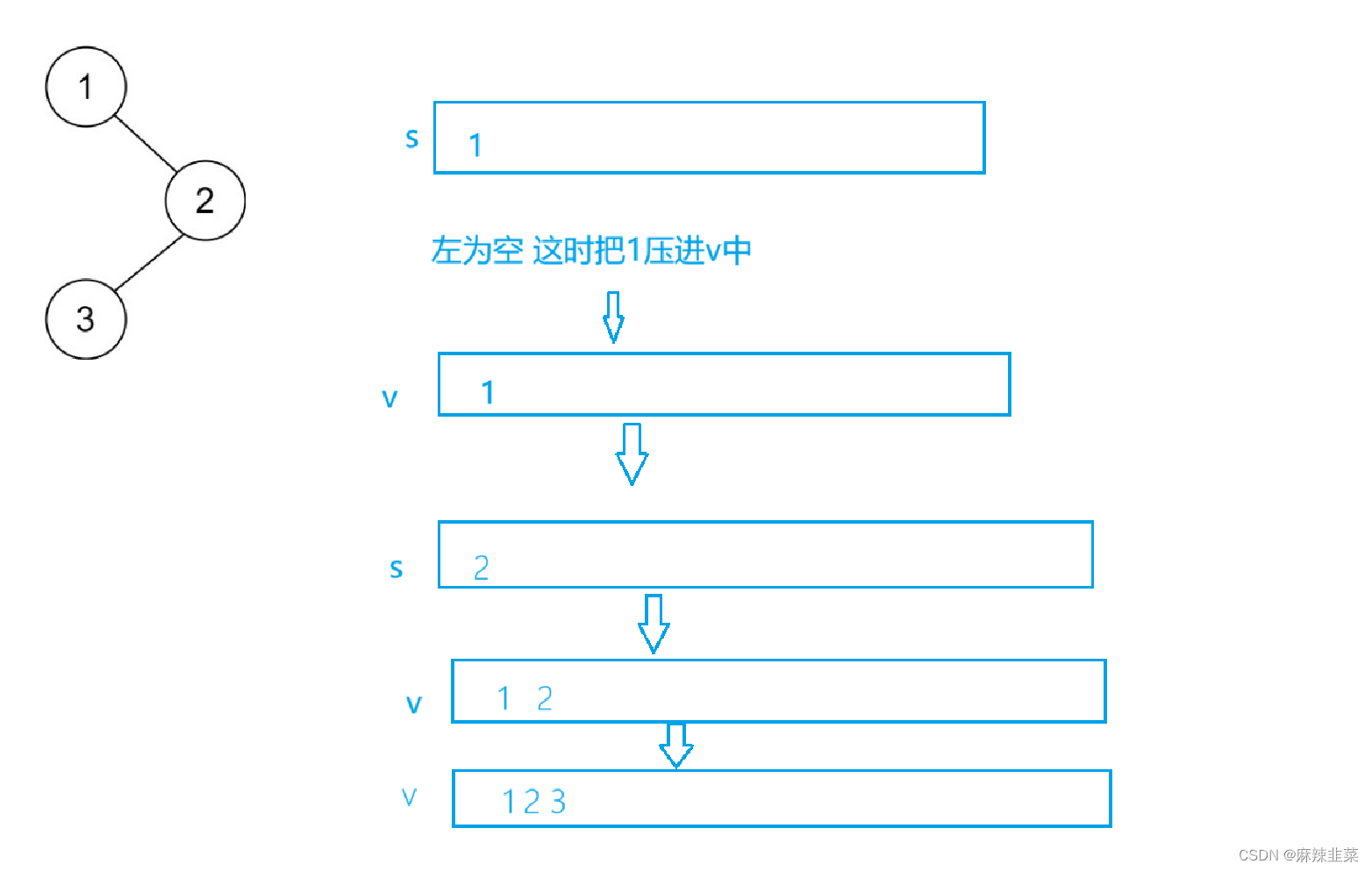
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> s;TreeNode* cur = root;while(cur || !s.empty()){while(cur){s.push(cur);cur = cur->left;}TreeNode* top = s.top();s.pop();v.push_back(top->val);cur = top->right;}return v;}
};

10. 二叉树的后序遍历，非递归迭代实现。145. 二叉树的后序遍历 - 力扣（LeetCode）

解题思路：后序先左再右然后根右为空了再取栈顶的元素，这里不一样的是如果左右都不空怎么访问根? 看下图

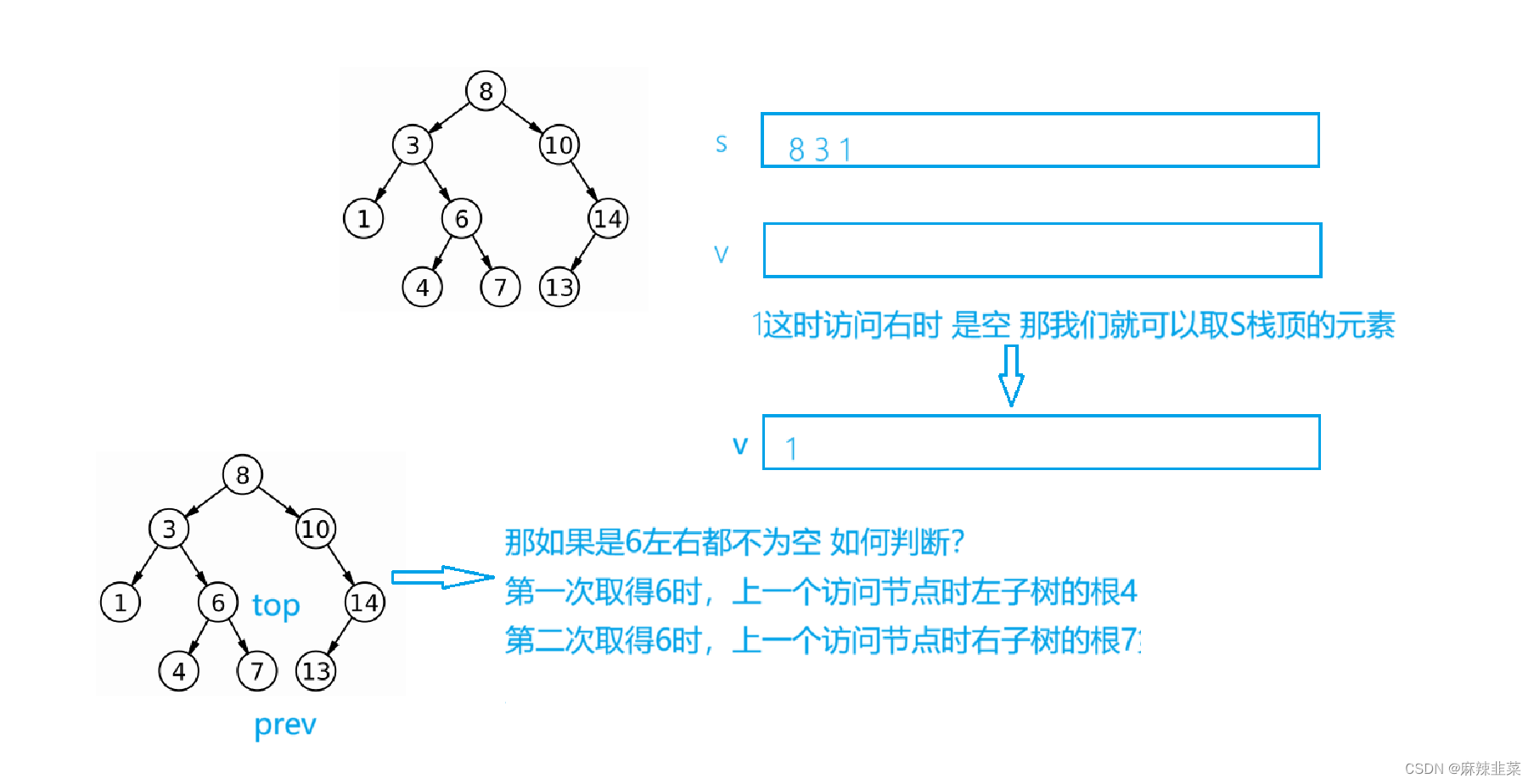
从这个图可以说明上一个访问的节点如果等于我的右子树的根，那我不就是根吗？

class Solution {
public:vector<int> postorderTraversal(TreeNode* root){vector<int> v;stack<TreeNode*> s;TreeNode* cur = root;TreeNode* prev = nullptr;while(cur || !s.empty()){while(cur){s.push(cur);cur = cur->left;}TreeNode* top = s.top();if(top->right == nullptr || top->right == prev){   v.push_back(top->val);s.pop();prev = top;}elsecur = top->right;}return v;}};