Dijkstra堆优化

Dijkstra算法是一种用于解决单源最短路径问题的算法，即从图中的一个顶点出发到所有其他顶点的最短路径。然而，处理大图时，常规的Dijkstra算法可能会遇到性能问题。这就是Dijkstra的堆优化算法派上用场的地方。在堆优化版本中，我们使用优先队列（通常是二叉堆）来获取当前未访问顶点中的最短距离顶点。这大大提高了算法的效率，因为每次从集合中获取最短距离的顶点的时间复杂度从降低到了，其中是顶点的数量。

前置知识

图是一种非线性数据结构，由节点（或顶底）和边组成。有多种方式可以表示图的数据结构。常见的有两种图的存储方式：

邻接矩阵

邻接矩阵是一种二维数组，其中的每个元素表示两个顶点之间是否存在边。如果顶点 i 和顶点 j 之间存在边，则matrix[i][j] = 1，否则matrix[i][j] = 0。

优点：

• 表示简单，直观；
• 对于无向图，邻接矩阵是对称的；
• 适用于稠密图（边数接近顶点数平方的图）。

缺点

• 对于稀疏图（边数远小于顶点数平方的图），邻接矩阵可能会浪费空间；
• 需要的空间，其中 n 是顶点数。

邻接表

邻接表是一种数组和链表的混合数据结构。邻接表中的每个元素都是一个链表，表示与该顶点相连的所有顶点。

优点：

• 适用于稀疏图，空间效率高；
• 可以容易地找到与特定顶点相邻的所有顶点。

缺点：

• 对于无向图，每条边都需要存储两次；
• 需要更复杂的数据结构来存储和管理。

C++中的图可以使用STL的vector来表示：

/*邻接矩阵*/
#include <iostream>
#include <vector>using namespace std;int main(){// 创建一个5*5的邻接矩阵vector<vector<int> > adjMatrix(5, vector<int> (5, 0));// 添加边adjMatrix[0][1] = 1;adjMatrix[1][0] = 1;return 0;
}

/*邻接表*/
#include <iostream>
#include <vector>using namespace std;int main(){//创建一个邻接表vector<vector<int> > adjList(5);//添加边adjList[0].push_back(1);adjList[1].push_back(0);return 0;
}

链式前向星（更适合算法竞赛）

链式前向星是一种存储图的方式，它结合了邻接矩阵和邻接表的优点，通过两个一维数组来保存图的信息，空间负责度低，方便边的遍历，适合存储稀疏图。

链式前向星存储图的方式如下：

h[ ]数组：h[ver]表示节点 ver 的第一条边的编号；

e[ ]数组：e[i]表示编号为 i 的边的终点；

w[ ]数组：w[i]表示编号为 i 的边的权重；

ne[ ]数组：ne[I]表示编号为 i 的边的下一条边的编号。

在C++中，我们可以使用数组来表示链式前向星：

int h[N], e[M], w[M], ne[M], idx;// 添加从a到b的边，初始时a指向空值
void add(int a, int b){// 分配空间idx，idx的ne[]指针指向初始时a指向的空值，头h[a]指向idx,idx更新e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}// 添加从a到b的边，权重为c
void add(int a, int b, int c){e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int main(){add(1, 2)memset(h, -1, sizeof h);// 输出节点1的所有邻居(i≠-1继续，否则就是指向空值了)for(int i = h[1]; ~i; i = ne[i]){int j = e[i];cout << j << ' ';}return 0;
}

图示：

优先队列入门

优先队列是一种抽象数据类型，它与常规队列非常相似，但在这种情况下，每个元素都有一定的优先级。在优先队列中，优先级最高的元素最先被删除。

在C++中，我们可以使用STL中的 priority_queue 来实现优先队列：

#include <iostream>
#include <queue>
using namespace std;int main(){priority_queue<int> pq;//默认大数优先pq.push(30);pq.push(100);pq.push(25);pq.push(40);//显示优先对列while(!pq.empty()){cout << pq.top() << '\n';pq.pop();}return 0;
}

使用自定义排序规则的优先队列

有时我们需要根据特定的排序规则来构建优先对列，而不是默认的排序规则。在C++中，我们可以通过定义比较函数来实现自定义排序规则：

#include <iostream>
#include <queue>
using namespace std;struct Compare{bool operator()(const int& a, const int& b){return a > b; //小数优先}
};int main(){priority_queue<int, vector<int>, Compare> pq;//结构体为向量容器pq.push(30);pq.push(100);pq.push(25);pq.push(40);//显示优先对列while(!pq.empty()){cout << pq.top() << '\n';pq.pop();}return 0;
}

使用二元组的自定义排序规则的优先队列

在C++中，我们可以通过为pair定义比较函数来实现自定义排序：

#include <iostream>
#include <queue>
#define x first
#define y second
using namespace std;struct Compare{bool operator()(const pair<int, int>& a, const pair<int, int>& b){return a.second < b.second; //第二个元素大优先}
};int main(){priority_queue<pair<int, int>, vector<pair<int, int>>, Compare> pq;pq.push(make_pair(1,30));pq.push(make_pair(2,100));pq.push(make_pair(3,25));pq.push(make_pair(4,40));//显示优先队列while(!pq.empty()){cout << "("<< pq.top().first<<","<<pq.top().second<<")\n";pq.pop();}return 0;
}

朴素版

基本思想

Dijkstra算法是一种用于解决单源最短路径问题的贪心算法。其基本思想如下：

        1.初始化：初始时，源节点的最短路径长度设为0（dist[source] = 0）。对于所有其他节点，我们暂时将最短路径长度设为无穷大（dist[v] = ∞），表示我们还不知道到达它们的最短路径。同时我们创建一个空集合，用来存放已经确定最短路径的节点。

        2.选择最小的 dist 节点：在未被确定最短路径的节点中，选择一个距离最小的节点 u。由于最开始只有源节点的最短路径是已知的，所以在第一步中，我们会选择源节点。

        3.更新路径长度：然后，我们更新所有从 u 直接连线到的节点的最短路径长度。假设 v 是从 u 出发可以直接到达的一个结点，如果通过 u 到 v 的路径 dist[u] + length(u, v) 比当前的 dist[v] 更短，那么我们就用新的路径长度来更新 dist[v]。

        4.重复：我们将 u 添加到已确定最短路径的节点集合中。然后再去未确定最短路径的节点中找一个距离最小的节点，继续进行更新。重复这个步骤，直到所有的节点都被添加到已确定最短路径的节点集合中。

通过这种方式，Dijkstra算法保证了每次添加到集合的节点都是当前可以确定最短路径的节点。需要注意的是，Dijkstra算法不能处理存在负权边的图，因为这会导致它可能再添加节点到集合之前就已经确定了一个更短的路径。对于存在负权边的图，我们通常使用Bellman-Ford算法或者Floyd-Warshall算法。

/*伪代码*/
函数 Dijkstra()初始化 dist[] 为无穷大dist[1] = 0对于 i = 0 到 n-1t = -1对于 j = 1 到 n如果节点 j 还未被访问 并且 t 不存在或者 dist[j] 更小则 t = j //找到最短路径点标记 t 已被访问对于 j = 1 到 n更新 dist[j] 为 dist[j] 和 dist[t] + edge[t][j] 的最小值如果 dist[n] 仍然为无穷大，返回 -1否则，返回 dist[n]

/*C++*/
int dijkstra(){memset(dist, 0x3f, sizeof dist);dist[1] = 0for(int i = 0; i < n; i++){int t = -1;for(int j = 1; j <= n; i++)if(!st[j] && (t = -1 || dist[t] > dist[j]))t = jst[t] = true;for(int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]);}return dist[n] == 0x3f3f3f3f ? -1 : dist[n];
}

Dijkstra的堆优化算法的步骤如下：

        1.初始时，我们将起点的距离设为0，将所有其他顶点的距离设为无穷大（在代码中，这通常用一个大的数字表示）。我们将所有顶点放入优先队列中。

        2.然后，我们从优先队列中取出一个距离最短的顶点。我们将这个顶点标记为已访问。

        3.接下来，我们遍历从这个顶点出发的所有边。对于每条边，我们检查是否可以通过这条边到达的顶点的距离比原来顶点的距离路径会更短。如果可以，我们就更新这个顶点的距离，并在优先队列中更新这个顶点的位置。

        4.我们重复上述步骤，直到优先队列为空，即所有可达的顶点都已访问过，或者找到目标顶点的最短路径。

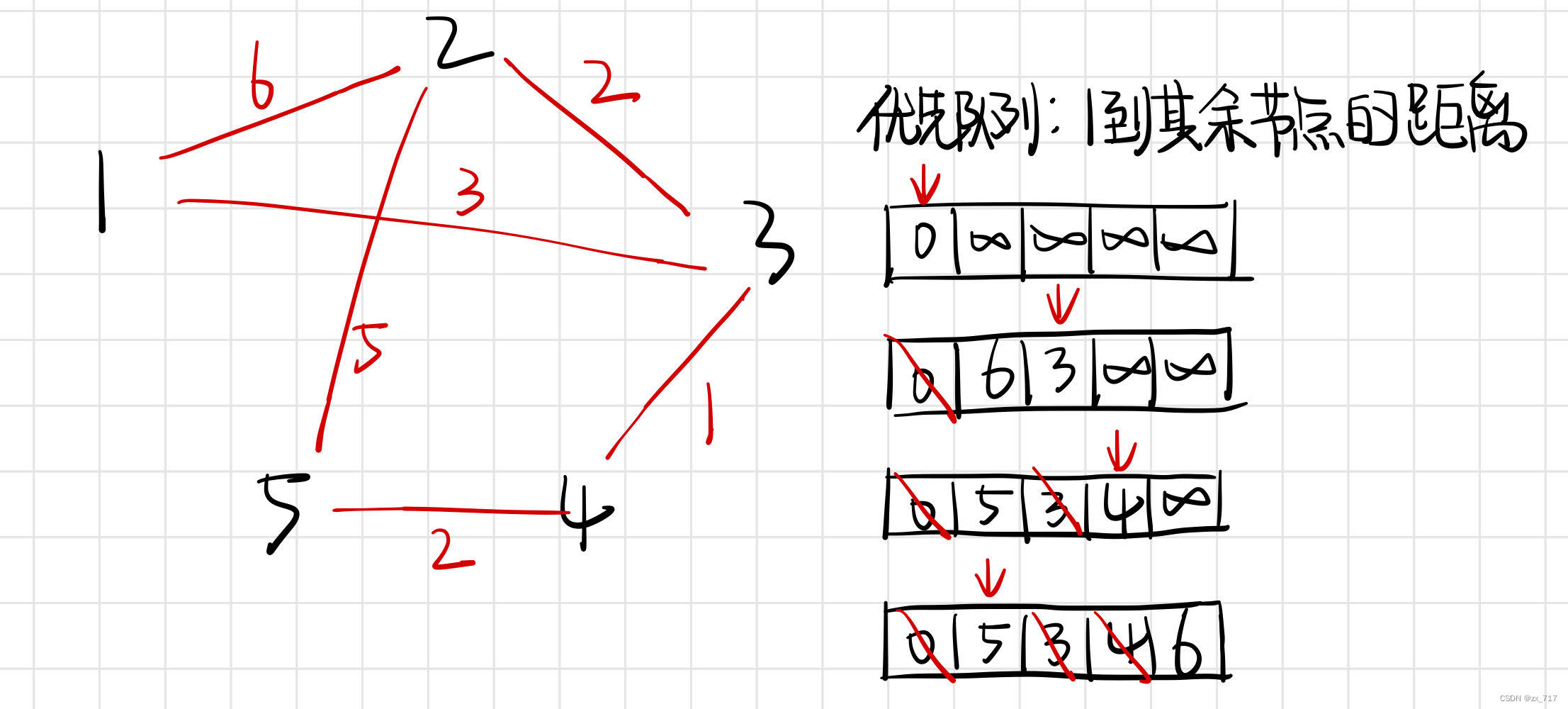
假设我们有一个图，它包含了5个顶点（1, 2, 3, 4, 5）和6条边。边的信息如下：1-2（权重6），1-3（权重3），2-3（权重2），3-4（权重1），2-4（权重5），4-5（权重2）。如果我们要找到从顶点 1 到所有其他顶点的最短路径，我们可以按照以下步骤进行：

        1.将所有顶点的距离初始化为无穷大，除了起点1，它的距离为0。所以，优先队列为：（1,0）（2,∞）（3,∞）（4,∞）（5,∞）。

        2.从队列中取出距离最小的顶点，这是1。然后，我们查看所有从1开始的边，我们发现顶点2和3的距离可以更新。所以，优先队列更新为：（2,6）（3,3）（4,∞）（5,∞）。

        3.我们再次从队列中取出距离最小的顶点，这是3。然后，我们查看从3开始的边，我们发现顶点2和4的距离可以更新。所以，优先队列更新为：（2,5）（4,4）（5,∞）。

        4.我们继续这个过程，直到队列为空。最后，我们得到了从顶点1到所有其他顶点的最短距离：1-2（距离5），1-3（距离3），1-4（距离4），1-5（距离6）。

代码

/*伪代码*/
设定顶点数 n，边数 m
设定存储图的数组 h[N], e[N], w[N], ne[N], 初始化索引 idx
设定存储最短距离的数组 dist[N]
设定标记数组 st[N]定义函数 dijkstra:初始化 dist 数组为无穷大建立优先队列 q, 队列元素为一对整数(距离, 顶点), 按距离从小到大排序设定起点 1 的距离为 0将(0, 1)推入队列 q当队列 q 不为空时:弹出队列顶部元素 t，设定顶点 ver 和距离 distance如果顶点 ver 已经被标记过，则继续下一轮循环否则，标记顶点 ver遍历顶点 ver 的所有领边:设定邻边的目标顶点为 j如果到达 j 的距离大于到达 ver 的距离加上边的权重w[i]，则更新
到达 j 的距离，并将(dist[j], j)推入队列 q如果终点 n 的距离为无穷大，返回-1否则，返回终点 n 的距离

/*C++*/
int n, m;
const int N = 1e3 + 10;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool st[N];
typedef pair<int, int> PII;int dijkstra(){memset(dist, 0x3f, sizeof dist);priority_queue<PII, vector<PII>, greater<PII>> q;dist[1] = 0;q.push({0, 1});while(!q.empty()){auto t = q.top();q.pop();auto ver = t.y, distance = t.x;if (st[ver])continue;st[ver] = true;//h[]第一条边,ne[]下一条边,e[]边指向的终点,w[]边的权重for(int i=h[ver]; i!=-1; i=ne[ver]){int j = e[i];if(dist[j] > dist[ver] + w[i]){dist[j] = dist[ver] + w[i];q.push({dist[j], j});}}}return dist[n] == 0x3f3f3f3f ? -1 : dist[n];
}

蓝桥王国

题目描述

小明是蓝桥王国的王子，今天是他登基之日。在即将成为国王之前，老国王给他出了道题，他想要考验小明是否有能力管理国家。内容如下：

蓝桥王国一共有N个建筑和M条单向道路，每条道路都连接这两个建筑，每个建筑都有自己编号，分别为1~N。（其中皇宫的编号为1）

国王想让小明回答从皇宫到每个建筑的最短路径是多少，但紧张的小名此时已经无法思考，请你编写程序帮助小明回答国王的考核。

输入描述

输入第一行包含两个正整数N, M。

第2到M+1行每行包含三个正整数u, v, w，表示u→v之间存在一条距离为w的路。

输出描述

输出仅一行，共N个数，分别表示从皇宫到编号为1~N建筑的最短距离，两两之间用空格隔开。（如果无法达到则输出-1）

输入输出样例

示例 1

输入

3 3 
1 2 1
1 3 5
2 3 2

输出

0 1 3

运行限制

语言	最大运行时间	最大运行内存
C++	2s	512M
C	2s	512M
Python3	2s	512M
Java	2s	512M

代码

#include <iostream>
#include <queue>
#include <cstring>    //memset
#include <algorithm>#define x first
#define y secondusing namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;int n, m;
const int N = 3e5 + 10, M = 1e6 + 10;
//节点的第一条边，指向的终点，下一条边
int h[N], e[M], ne[M], idx;
LL w[M], dist[N];
bool st[N];void dijkstra(){memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PLI, vector<PLI>, greater<PLI>> heap;heap.push({0,1});while(!heap.empty()){auto t = heap.top();heap.pop();LL ver = t.y, distance = t.x;if(st[ver])continue;st[ver] = true;for(int i = h[ver]; i != -1; i = ne[i]){LL j = e[i];if(dist[j] > dist[ver] + w[i]){dist[j] = dist[ver] + w[i];heap.push({dist[j], j});}}}
}void add(LL a, LL b, LL c){//分配内存idx, 插入链表（头插法）, 加权重e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int main(){cin >> n >> m;//初始化链表指向空值-1memset(h, -1, sizeof h);for(int i = 0; i < m; i++){LL a, b, c;cin >> a >> b >> c;add(a, b, c);//放入链表}dijkstra();for(int i = 1; i <= n; i++){cout << (dist[i]==0x3f3f3f3f3f3f3f3f ? -1:dist[i]) << " ";}cout << endl;return 0;
}

总结

Dijkstra算法是最短路径的一个重要解法，但是只能用于正值带权。