💕"对相爱的人来说，对方的心意，才是最好的房子。"💕
作者：Lvzi
文章主要内容：算法系列–递归,回溯,剪枝的综合应用(1)

大家好,今天为大家带来的是算法系列--递归,回溯,剪枝的综合应用(1)

1.全排列(重点)

链接:
https://leetcode.cn/problems/permutations/description/

分析:

1.画出决策树

所谓的决策树就是我们小时候学排列画的树状图,通过一个树枚举出所有的情况

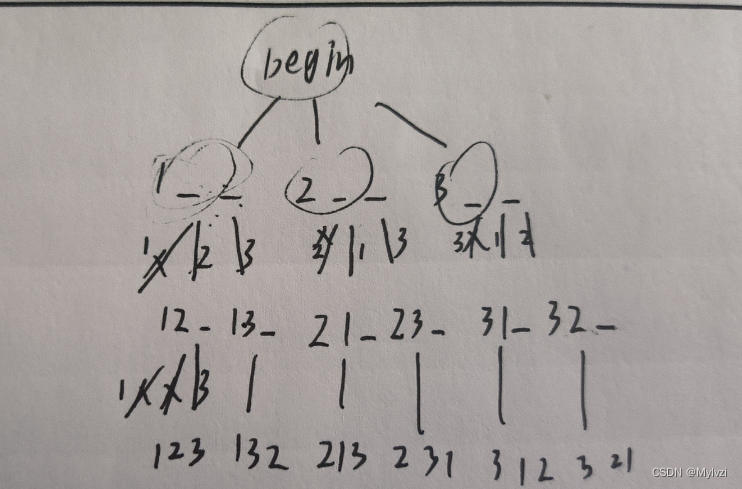
画出决策树之后,分析每一层干的事情是否相同(一般都是相同的),对于本题,每一层干的事可以总结为

• 枚举出所有符合条件的排列情况

注意:决策树画的越详细越好(包括所有不符合条件的情况也画出来),有助于我们后面设计代码

2.设计代码

设计代码主要从两个方面考虑

1. 全局变量
2. dfs函数

1.全局变量

模拟决策的过程,想想需要哪些变量,首先题目要求的返回值是一个二维数组,所以需要设计一个ret作为返回值,当我们在枚举出所有的情况时,要考虑到枚举的数字是否被使用,如果被使用就不能被枚举,所以要标记搜索路径上数字的使用情况,所以要创建一个布尔类型的数组,接着当我们走到叶子结点时,需要保存当前排列的情况,一共就三个数字,所以需要使用一个数组进行保存,接着当从叶子结点向上返回时,我们需要舍弃掉数组中最后一个数字,这个操作比较简单,可以直接对数组进行变动即可

• List<List> ret: 最后的返回值,用于记录所有排列情况
• List path: 用于记录每一次dfs的结果
• boolean[] check : 用于标记搜索过程中数字的使用情况

2.dfs函数

和递归相同,dfs函数的设计我们只需要关注某一个子问题的具体操作即可

把数组中所有的数都枚举一遍,只要没有用过,就添加到path后面

3.细节问题

• 剪枝:在check中被标记为true,就进行剪枝

• 回溯:如图
  

• 递归出口:当path中元素的数目和nums中元素的数目相同时,递归结束,将path中的所有元素添加到ret之中

4.代码实现

class Solution {// 全局变量List<List<Integer>> ret;// 返回值List<Integer> path;// 记录搜索路径boolean[] check;// 标记是否被使用过public List<List<Integer>> permute(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];dfs(nums);return ret;}public void dfs(int[] nums) {// 递归出口if(nums.length == path.size()) {ret.add(new ArrayList<>(path));return;}// 函数体for(int i = 0; i < nums.length; i++) {if(check[i] == false) {path.add(nums[i]);check[i] = true;dfs(nums);// 回溯check[i] = false;path.remove(path.size() - 1);}}}
}

为什么不是ret.add(path);

2.⼦集

链接:
https://leetcode.cn/problems/subsets/description/

分析:
画决策树:

根据定义选或者不选当前数

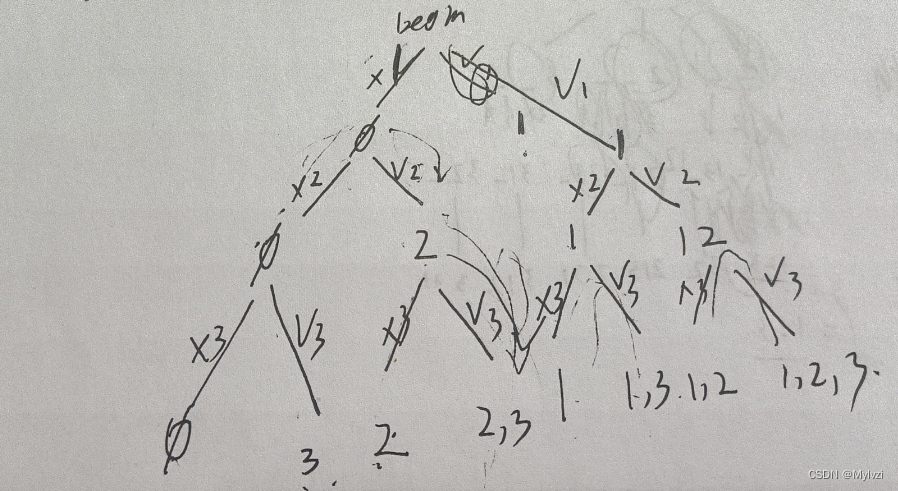
每一层都在干啥
分别枚举出选当前数字选和不选当前数的所有情况

设计代码:

全局变量:模拟整个过程,需要两个变量

• ret:接收每次搜索的结果,是最终的返回值
• path: 表示搜索路径的结果

dfs: 需要一个数组和当前的位置(下标),因为我需要知道当前的数是谁

细节问题:

• 剪枝:不需要
• 回溯:只有当选择选当前数的情况时,在返回的时候需要删除这个数
• 递归出口:当pos走到n.length时表示数组遍历完毕,结束递归,将path添加进ret之中

代码:

class Solution {// 全局变量List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int pos) {// 递归出口if(pos == nums.length) {ret.add(new ArrayList<>(path));return;}// 选path.add(nums[pos]);dfs(nums,pos + 1);path.remove(path.size() - 1);// 回溯// 不选dfs(nums,pos + 1);}
}

这种决策树的遍历类似于二叉树遍历中的后序遍历

第二种决策树

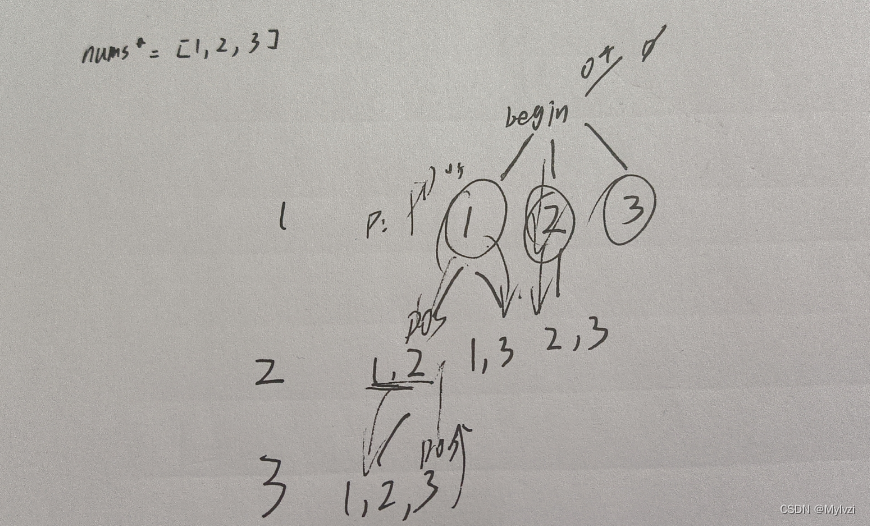
以当前位置的值为起始位置,枚举出后面所有的数字的情况

class Solution {// 全局变量List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int pos) {// 这个遍历类似于前序遍历  根左右ret.add(new ArrayList<>(path));// 刚进来的时候path为空 空集也是子集的一种// 从当前位置一直遍历到结束for(int i = pos; i < nums.length; i++) {path.add(nums[i]);dfs(nums,i+1);path.remove(path.size() - 1);// 回溯}}
}

这种遍历的方式类似于二叉树遍历中的前序遍历,先打印根节点的值,再去遍历左右子树

总结:

1. 画出具体详细的决策树,模拟每一步都是在干啥,明确操作
2. 设计代码,具体来说是要设计出需要的全局变量和dfs,设计dfs和我们之前递归过程中设计函数头,函数体,递归出口一样,这不过这里的逻辑会更加的复杂一点
3. 注意细节问题:主要从两个方面考虑
   • 剪枝
   • 回溯

3.找出所有⼦集的异或总和再求和

链接:
https://leetcode.cn/problems/sum-of-all-subset-xor-totals/

分析:

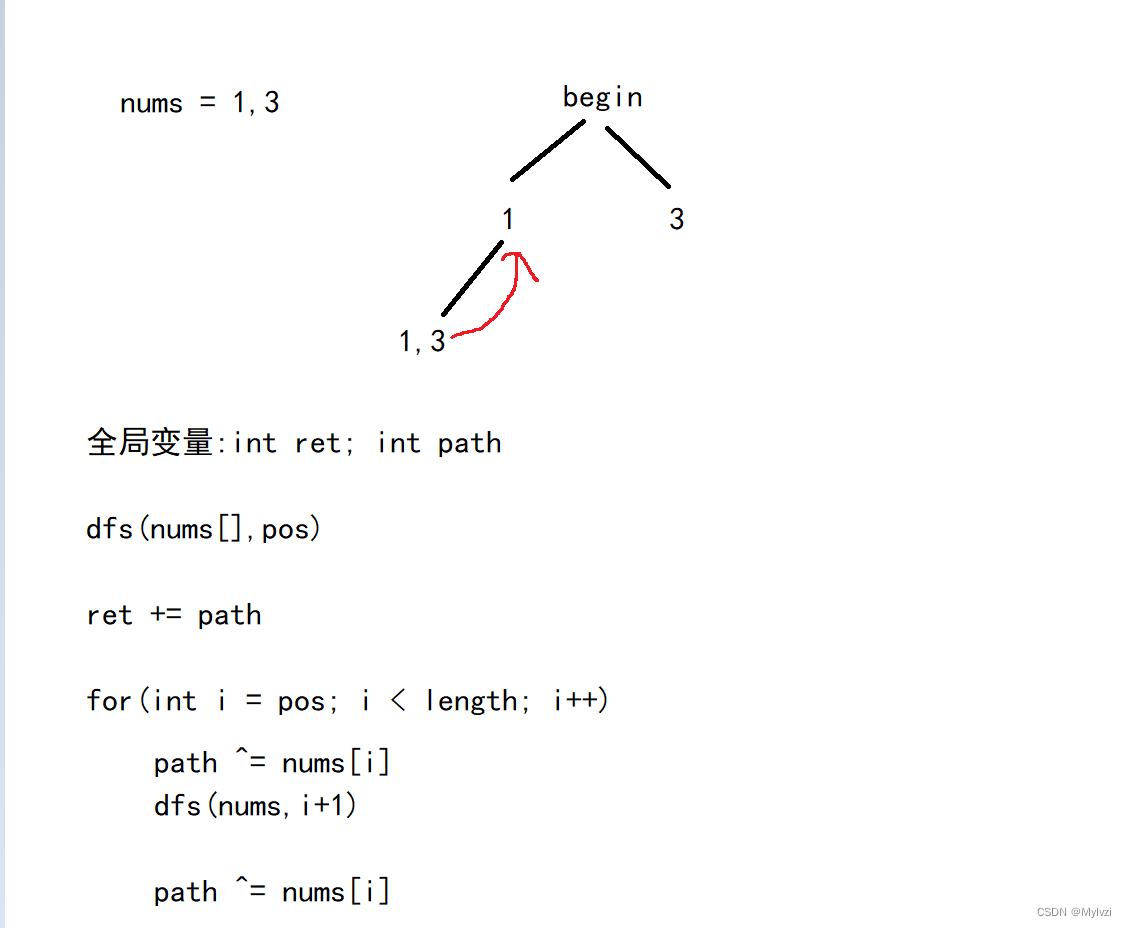
代码:

class Solution {// 全局变量int ret;int path;public int subsetXORSum(int[] nums) {dfs(nums,0);return ret;}public void dfs(int[] nums,int pos) {ret += path;for(int i = pos; i < nums.length; i++) {path ^= nums[i];dfs(nums,i + 1);// 递归下一个位置path ^= nums[i];// 回溯}}
}

注意这里面利用了^运算的性质,a ^ a = 0

还是那句话,画出决策树一切都好办!!!

四.全排列II

链接:
https://leetcode.cn/problems/permutations-ii/

分析:

相较于全排列I多了个限制条件不能有重复的组合出现,那么只需分析出所有的不合法的情况即可

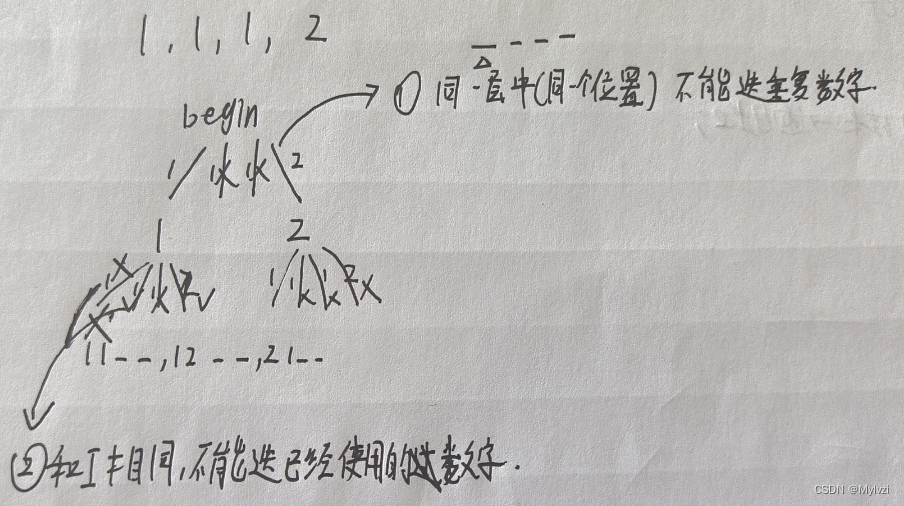
1. 同一层中(同一位置比如选择第一个位置的数),不能选择重复的数字
2. 和全排列I一样,不能选择已经使用过的数字

对于2的处理和全排列I的处理方式相同,使用一个布尔类型的check数组标记即可,对于1需要判断出 不合法的数据,首先要和前面的数字相同nums[i] == nums[i - 1],i不能越界i != 0,其次上述两个条件还不能完全判定出是不合法的数据,还必须要保证前一个数字是同一层的,check[i - 1] == false

总结来说就是:

1. nums[i] == nums[i-1] && 在同一层–>不合法数据–>不能dfs
2. nums[i] == nums[i-1] && 不在同一层–>合法数据–>能dfs

此外,为了保证相同的数据是紧挨着的,还需要进行排序

代码:

class Solution {// 全局变量List<List<Integer>> ret;// 返回值List<Integer> path;// 记录搜索路径boolean[] check;// 标记是否被使用过public List<List<Integer>> permuteUnique(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];Arrays.sort(nums);dfs(nums);return ret;}public void dfs(int[] nums) {// 递归出口if(path.size() == nums.length) {ret.add(new ArrayList<>(path));return;}// 函数体for(int i = 0; i < nums.length; i++) {// 剪枝  不合法的数据if(check[i] == true || (i != 0 && nums[i] == nums[i - 1] && check[i - 1] == false)) {continue;}path.add(nums[i]);check[i] = true;dfs(nums);// 回溯check[i] = false;path.remove(path.size() - 1);}}
}

5.电话号码的字⺟组合

链接:
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/
分析:

每一层所做的事情:

• 枚举出当前数字对应的字符串中所有的字符

设计代码:
1.全局变量
ret:返回值
path
string[] map:映射关系

2.dfs(digits,pos)
pos表示digits中字符的下标
递归出口:
走到最后一个节点的位置

回溯:
删除最后添加的数字

剪枝:无

代码:

class Solution {List<String> ret;// 返回值StringBuffer path;// 记录搜索路径String[] map= {"","","abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};// 建立映射关系public List<String> letterCombinations(String digits) {ret = new ArrayList<>();path = new StringBuffer();if(digits.length() == 0) return ret;// 处理为空的情况dfs(digits,0);return ret;}private void dfs(String digits, int pos) {if(pos == digits.length()) {// 递归出口ret.add(path.toString());return;}String s = map[digits.charAt(pos) - '0'];// 获取当前层的字符串for(int i = 0; i < s.length(); i++) {path.append(s.charAt(i));// 追加字符dfs(digits, pos + 1);path.deleteCharAt(path.length() - 1);// 回溯}}
}

dfs是往下,是递归,每一层是要做的事情是子问题