【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结12
25.零钱兑换 II
题目链接:518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
提示:
1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000
题解:
方法:完全背包
使用动态规划解决零钱兑换问题,采用完全背包的思想。
设计一维数组f,其中f[j]表示凑出金额j的组合数。
初始化数组f,将f[0]设置为1,表示凑出金额0的组合数为1。
通过状态转移方程更新数组f的值,即f[j] += f[j - val],其中val为硬币的面值,表示凑出金额j的组合数等于凑出金额j - val的组合数加上当前硬币的组合数。
最终返回f[cnt],即使用所有硬币凑出金额cnt的组合数。
class Solution {// 使用动态规划解决零钱兑换问题(完全背包)public int change(int cnt, int[] cs) {int[] f = new int[cnt + 1]; // 定义一维数组f,表示凑出金额j的组合数f[0] = 1; // 初始化凑出金额0的组合数为1// 动态规划状态转移过程,更新数组f的值for (int val : cs) { // 遍历硬币面值数组for (int j = val; j <= cnt; j++) { // 遍历金额范围f[j] += f[j - val]; // 更新组合数}}return f[cnt]; // 返回使用所有硬币凑出目标金额的组合数}
}
方法:完全背包 (优化)
class Solution {// 使用动态规划解决零钱兑换问题(完全背包,一维优化)public int change(int cnt, int[] cs) {int[] f = new int[cnt + 1]; // 定义一维数组f,表示凑出金额j的组合数f[0] = 1; // 初始化凑出金额0的组合数为1// 动态规划状态转移过程,更新数组f的值for (int val : cs) { // 遍历硬币面值数组for (int j = val; j <= cnt; j++) { // 遍历金额范围f[j] += f[j - val]; // 更新组合数}}return f[cnt]; // 返回使用所有硬币凑出目标金额的组合数}
}26.设计可以求最短路径的图类
题目链接:2642. 设计可以求最短路径的图类
给你一个有 n 个节点的 有向带权 图,节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示,其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。
请你实现一个 Graph 类:
- Graph(int n, int[][] edges) 初始化图有 n 个节点,并输入初始边。
- addEdge(int[] edge) 向边集中添加一条边,其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
- int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在,返回 -1 。一条路径的代价是路径中所有边代价之和。
示例 1:
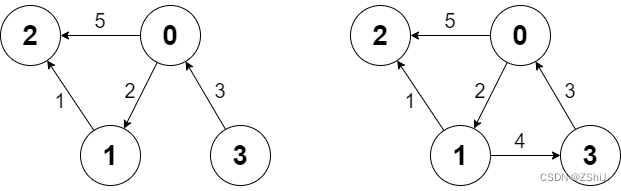
输入:
[“Graph”, “shortestPath”, “shortestPath”, “addEdge”, “shortestPath”]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3],
[[1, 3, 4]], [0, 3]]输出:
[null, 6, -1, null, 6]
解释:
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示:3 -> 0 -> 1 -> 2
,总代价为 3 + 2 + 1 = 6 。g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边,得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ,总代价为 2 + 4
= 6 。
提示:
1 <= n <= 100
0 <= edges.length <= n * (n - 1)
edges[i].length == edge.length == 3
0 <= fromi, toi, from, to, node1, node2 <= n - 1
1 <= edgeCosti, edgeCost <= 106
图中任何时候都不会有重边和自环。
调用 addEdge 至多 100 次。
调用 shortestPath 至多 100 次。
题解:
方法:Dijkstra
直接把边addEdge加入图中即可。
对于 shortestPath,用 Dijkstra 算法计算从起点 start 到终点 end 的最短路长度。
邻接矩阵建图 + 朴素 Dijkstra
class Graph {private static final int INF = Integer.MAX_VALUE / 2; // 防止更新最短路时加法溢出private final int[][] g; // 邻接矩阵表示图的边信息// 构造方法,初始化图的邻接矩阵并添加边public Graph(int n, int[][] edges) {g = new int[n][n]; // 初始化邻接矩阵for (int[] row : g) {Arrays.fill(row, INF); // 初始化邻接矩阵的值为无穷大}for (int[] e : edges) {addEdge(e); // 添加一条边(题目保证没有重边)}}// 添加一条边到邻接矩阵public void addEdge(int[] e) {g[e[0]][e[1]] = e[2]; // 添加一条边(题目保证这条边之前不存在)}// 求解从起点到终点的最短路径长度public int shortestPath(int start, int end) {int n = g.length;int[] dis = new int[n]; // 起点到各个点的最短路径长度Arrays.fill(dis, INF); // 初始化为无穷大dis[start] = 0; // 起点到自身的距离为0boolean[] vis = new boolean[n]; // 标记节点是否被访问过while (true) {int x = -1; // 最近的未访问节点for (int i = 0; i < n; i++) {if (!vis[i] && (x < 0 || dis[i] < dis[x])) {x = i;}}if (x < 0 || dis[x] == INF) { // 所有从起点能到达的点都被更新了return -1; // 终点无法到达}if (x == end) { // 找到终点,提前退出return dis[x]; // 返回终点的最短路径长度}vis[x] = true; // 标记节点为已访问for (int y = 0; y < n; y++) {dis[y] = Math.min(dis[y], dis[x] + g[x][y]); // 更新最短路径长度}}}
}邻接表建图 + 堆优化 Dijkstra
class Graph {private final List<int[]>[] g; // 邻接表表示图的边信息// 构造方法,初始化图的邻接表并添加边public Graph(int n, int[][] edges) {g = new ArrayList[n]; // 初始化邻接表Arrays.setAll(g, i -> new ArrayList<>()); // 初始化邻接表的数组for (int[] e : edges) {addEdge(e); // 添加一条边(题目保证没有重边)}}// 添加一条边到邻接表public void addEdge(int[] e) {g[e[0]].add(new int[]{e[1], e[2]}); // 添加一条边(题目保证这条边之前不存在)}// 求解从起点到终点的最短路径长度public int shortestPath(int start, int end) {int[] dis = new int[g.length]; // 起点到各个点的最短路径长度Arrays.fill(dis, Integer.MAX_VALUE); // 初始化为无穷大dis[start] = 0; // 起点到自身的距离为0PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[0] - b[0])); // 使用最小堆存储节点,按路径长度排序pq.offer(new int[]{0, start}); // 将起点加入优先队列while (!pq.isEmpty()) {int[] p = pq.poll(); // 弹出当前路径长度最短的节点int d = p[0]; // 当前路径长度int x = p[1]; // 当前节点if (x == end) { // 到达终点,返回最短路径长度return d;}if (d > dis[x]) { // x 之前出堆过,无需更新邻居的最短路continue;}for (int[] e : g[x]) {int y = e[0]; // 邻居节点int w = e[1]; // 边的权重if (d + w < dis[y]) { // 如果通过当前节点 x 到达邻居节点 y 的路径更短dis[y] = d + w; // 更新最短路径长度pq.offer(new int[]{dis[y], y}); // 将邻居节点加入优先队列}}}return -1; // 无法到达终点}
}
题单:Dijkstra 算法
2642. 设计可以求最短路径的图类
1514. 概率最大的路径
1631. 最小体力消耗路径
1368. 使网格图至少有一条有效路径的最小代价
1786. 从第一个节点出发到最后一个节点的受限路径数
1976. 到达目的地的方案数
2662. 前往目标的最小代价
2045. 到达目的地的第二短时间
882. 细分图中的可到达节点
2203. 得到要求路径的最小带权子图
2577. 在网格图中访问一个格子的最少时间
2699. 修改图中的边权
2093. 前往目标城市的最小费用
2473. 购买苹果的最低成本
2714. 找到最短路径的 K 次跨越
2737. 找到最近的标记节点
LCP 35. 电动车游城市
方法:Floyd
创建一个Graph类表示图结构,使用邻接矩阵存储图的边权重信息,并使用Floyd-Warshall算法求解任意两点之间的最短路径长度。
在构造方法中,初始化邻接矩阵,并根据边的信息更新图的边权重。然后,利用Floyd-Warshall算法计算任意两点之间的最短路径长度。
使用INF表示无穷大,防止加法溢出,初始化邻接矩阵的对角线为0,其他位置为INF。
构造方法中使用两层循环遍历所有节点对,并通过中间节点k更新从节点i到节点j的最短路径长度。
shortestPath方法用于返回从指定起点到终点的最短路径长度,如果路径不存在则返回-1。
addEdge方法用于添加一条边,并根据新添加的边更新图的最短路径长度。
class Graph {private static final int INF = Integer.MAX_VALUE / 3; // 防止更新最短路时加法溢出private final int[][] f; // 邻接矩阵表示图的边权重信息// 构造方法,初始化邻接矩阵,并使用Floyd-Warshall算法计算任意两点之间的最短路径长度public Graph(int n, int[][] edges) {f = new int[n][n]; // 初始化邻接矩阵for (int i = 0; i < n; i++) {Arrays.fill(f[i], INF); // 初始化邻接矩阵为无穷大f[i][i] = 0; // 对角线上的元素为0}for (int[] e : edges) {f[e[0]][e[1]] = e[2]; // 添加一条边(题目保证没有重边和自环)}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {if (f[i][k] == INF) {continue;}for (int j = 0; j < n; j++) {f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j]); // 使用中间节点k更新最短路径长度}}}}// 添加一条边,并根据新添加的边更新图的最短路径长度public void addEdge(int[] e) {int x = e[0], y = e[1], w = e[2], n = f.length;if (w >= f[x][y]) { // 如果新添加的边权重大于等于已有的边权重,则无需更新return;}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {f[i][j] = Math.min(f[i][j], f[i][x] + w + f[y][j]); // 更新最短路径长度}}}// 返回从指定起点到终点的最短路径长度,如果路径不存在则返回-1public int shortestPath(int start, int end) {int ans = f[start][end]; // 获取起点到终点的最短路径长度return ans < INF ? ans : -1; // 如果路径长度小于INF,则返回路径长度,否则返回-1}
}27.统计将重叠区间合并成组的方案数
题目链接:2580. 统计将重叠区间合并成组的方案数
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
-
每个区间只属于一个组。
-
两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间 [1, 3] 和 [2, 5] 有交集,因为 2 和 3 在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]]
输出:2
解释:
两个区间有交集,所以它们必须在同一个组内。
所以有两种方案:
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]]
输出:4
解释:
区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。
同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。
所以总共有 4 种分组方案:
- 所有区间都在第 1 组。
- 所有区间都在第 2 组。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
1 <= ranges.length <= 105
ranges[i].length == 2
0 <= starti <= endi <= 109
题解:
方法:合并区间
首先对ranges按照区间的起点进行升序排序,这样可以保证后面的区间起点始终不小于前面的区间起点。
初始化ans为1,用于记录合法区间的数量。初始化maxR为-1,用于记录当前能够合并的区间的最大右边界。
遍历排序后的ranges数组,对于每个区间p:
如果当前区间的起点p[0]大于maxR,说明当前区间无法与之前的区间合并,此时将ans乘以2并取模1_000_000_007,表示新增加一个独立的区间。
更新maxR为当前区间的右边界p[1],表示将当前区间合并到已有的区间中。
遍历结束后,返回ans作为结果。
注释已添加在代码中。
class Solution {public int countWays(int[][] ranges) {// 对ranges按照区间的起点进行升序排序Arrays.sort(ranges, (a, b) -> a[0] - b[0]);// 初始化ans为1,用于记录合法区间的数量int ans = 1;// 初始化maxR为-1,用于记录当前能够合并的区间的最大右边界int maxR = -1;// 遍历排序后的ranges数组for (int[] p : ranges) {// 如果当前区间的起点p[0]大于maxR,说明当前区间无法与之前的区间合并if (p[0] > maxR) {// 将ans乘以2并取模1_000_000_007,表示新增加一个独立的区间ans = ans * 2 % 1_000_000_007;}// 更新maxR为当前区间的右边界p[1],表示将当前区间合并到已有的区间中maxR = Math.max(maxR, p[1]);}// 返回ans作为结果return ans;}
}
题单:合并区间
难度1
56. 合并区间
55. 跳跃游戏
2963. 统计好分割方案的数目
2584. 分割数组使乘积互质
2585. 寻找最大长度的未覆盖区间
难度2
2587. 跳跃游戏 II
2588. 视频拼接
2589. 灌溉花园的最少水龙头数目
28.访问完所有房间的第一天
题目链接:1997. 访问完所有房间的第一天
你需要访问 n 个房间,房间从 0 到 n - 1 编号。同时,每一天都有一个日期编号,从 0 开始,依天数递增。你每天都会访问一个房间。
最开始的第 0 天,你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 nextVisit 。在接下来的几天中,你访问房间的 次序 将根据下面的 规则 决定:
- 假设某一天,你访问 i 号房间。
- 如果算上本次访问,访问 i 号房间的次数为 奇数 ,那么 第二天 需要访问 nextVisit[i] 所指定的房间,其中 0 <= nextVisit[i] <= i 。
- 如果算上本次访问,访问 i 号房间的次数为 偶数 ,那么 第二天 需要访问 (i + 1) mod n 号房间。
请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大,返回对 109+ 7 取余后的结果。
示例 1:
输入:nextVisit = [0,0]
输出:2
解释:
第 0 天,你访问房间 0 。访问 0 号房间的总次数为 1 ,次数为奇数。
下一天你需要访问房间的编号是 nextVisit[0] = 0
第 1 天,你访问房间 0 。访问 0 号房间的总次数为 2 ,次数为偶数。
下一天你需要访问房间的编号是 (0 + 1) mod 2 = 1
第 2 天,你访问房间 1 。这是你第一次完成访问所有房间的那天。
示例 2:
输入:nextVisit = [0,0,2]
输出:6
解释:
你每天访问房间的次序是 [0,0,1,0,0,1,2,…] 。
第 6 天是你访问完所有房间的第一天。
示例 3:
输入:nextVisit = [0,1,2,0]
输出:6
解释:
你每天访问房间的次序是 [0,0,1,1,2,2,3,…] 。
第 6 天是你访问完所有房间的第一天。
提示:
n == nextVisit.length
2 <= n <= 105
0 <= nextVisit[i] <= i
题解:
方法:前缀和优化 DP
利用前缀和数组 s[] 存储到达每个房间时已经停留的总天数。通过动态规划的方式,从第一个房间开始遍历到倒数第二个房间,计算到达下一个房间所需的天数,并将结果存储在前缀和数组中。最终返回到达最后一个房间所需的天数。
class Solution {public int firstDayBeenInAllRooms(int[] nextVisit) {final long MOD = 1_000_000_007; // 取模的值int n = nextVisit.length; // 房间数量long[] s = new long[n]; // 用于存储前缀和的数组// 循环计算前缀和for (int i = 0; i < n - 1; i++) {int j = nextVisit[i]; // 下一个要访问的房间s[i + 1] = (s[i] * 2 - s[j] + 2 + MOD) % MOD; // 计算当前房间所需的天数并取模,避免负数// s[i] 表示到达房间 i 时已经停留的总天数// s[i] * 2 表示离开房间 i 时已经停留的总天数(因为要走一趟再回来)// s[j] 表示到达下一个房间 j 时已经停留的总天数// (s[i] * 2 - s[j] + 2) 表示到达下一个房间需要的天数// 加 2 是因为无论如何都需要一天时间移动到下一个房间// 取模避免结果溢出}return (int) s[n - 1]; // 返回到达最后一个房间所需的天数}
}
29.元素和最小的山形三元组 I
题目链接:2908. 元素和最小的山形三元组 I
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 :
- i < j < k
- nums[i] < nums[j] 且 nums[k] < nums[j]
请你找出 nums 中 元素和最小 的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
示例 1:
输入:nums = [8,6,1,5,3]
输出:9
解释:三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组,因为:
2 < 3 < 4
nums[2] < nums[3] 且 nums[4] < nums[3]
这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。
示例 2:
输入:nums = [5,4,8,7,10,2]
输出:13
解释:三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组,因为:
1 < 3 < 5
nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
示例 3:
输入:nums = [6,5,4,3,4,5]
输出:-1
解释:可以证明 nums 中不存在山形三元组。
题解:
方法:O(n) 前后缀分解
首先从右往左计算数组的后缀最小值,然后从左往右遍历数组,寻找满足一定条件的山形结构。在遍历过程中,维护前缀的最小值,并判断当前元素是否构成山形结构,如果是,则更新答案。最后返回答案,若无满足条件的山形结构,则返回-1。
class Solution {public int minimumSum(int[] nums) {int n = nums.length;int[] suf = new int[n]; // 后缀最小值suf[n - 1] = nums[n - 1];// 计算后缀最小值for (int i = n - 2; i > 1; i--) {suf[i] = Math.min(suf[i + 1], nums[i]);}int ans = Integer.MAX_VALUE; // 初始答案为整型最大值int pre = nums[0]; // 前缀最小值// 寻找山形结构for (int j = 1; j < n - 1; j++) {if (pre < nums[j] && nums[j] > suf[j + 1]) { // 如果当前元素构成山形ans = Math.min(ans, pre + nums[j] + suf[j + 1]); // 更新答案}pre = Math.min(pre, nums[j]); // 更新前缀最小值}return ans == Integer.MAX_VALUE ? -1 : ans; // 返回最终答案,若无满足条件的山形结构则返回-1}
}
30.需要添加的硬币的最小数量
题目链接:2952. 需要添加的硬币的最小数量
给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值,以及一个整数 target 。
如果存在某个 coins 的子序列总和为 x,那么整数 x 就是一个 可取得的金额 。
返回需要添加到数组中的 任意面值 硬币的 最小数量 ,使范围 [1, target] 内的每个整数都属于 可取得的金额 。
数组的 子序列 是通过删除原始数组的一些(可能不删除)元素而形成的新的 非空 数组,删除过程不会改变剩余元素的相对位置。
示例 1:
输入:coins = [1,4,10], target = 19
输出:2
解释:需要添加面值为 2 和 8 的硬币各一枚,得到硬币数组 [1,2,4,8,10] 。
可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 2 。
示例 2:
输入:coins = [1,4,10,5,7,19], target = 19
输出:1
解释:只需要添加一枚面值为 2 的硬币,得到硬币数组 [1,2,4,5,7,10,19] 。
可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 1 。
示例 3:
输入:coins = [1,1,1], target = 20
输出:3
解释:
需要添加面值为 4 、8 和 16 的硬币各一枚,得到硬币数组 [1,1,1,4,8,16] 。
可以证明从 1 到 20 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 3 。
提示:
1 <= target <= 105
1 <= coins.length <= 105
1 <= coins[i] <= target
题解:
方法:贪心
归纳法
首先对硬币面额进行排序,然后从能够表示的最小金额 1 开始,逐步增加能够表示的金额范围,直到达到目标金额为止。在每次循环中,尽可能地使用已有的硬币,如果当前没有合适的硬币可用,则必须添加当前能够表示的金额,然后将能够表示的金额范围扩大为原来的两倍。最终返回所添加的硬币数量,即为最少需要添加的硬币数量。
class Solution {public int minimumAddedCoins(int[] coins, int target) {Arrays.sort(coins); // 对硬币面额进行排序int ans = 0; // 记录添加的硬币数量int s = 1; // 当前能够表示的金额范围int i = 0; // 当前遍历到的硬币面额的索引// 当能够表示的金额范围小于或等于目标金额时,继续循环while (s <= target) {// 如果还有硬币可用并且当前硬币的面额不超过能够表示的金额范围if (i < coins.length && coins[i] <= s) {s += coins[i++]; // 使用当前硬币,更新能够表示的金额范围} else {s *= 2; // 如果没有合适的硬币可用,则必须添加 s 这个金额ans++; // 记录添加的硬币数量}}return ans; // 返回添加的硬币数量}
}
31. 验证二叉树的前序序列化
题目链接:331. 验证二叉树的前序序列化
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
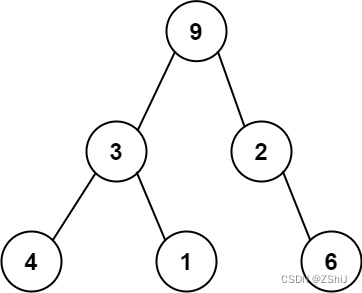
例如,上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”,其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。
你可以认为输入格式总是有效的
例如它永远不会包含两个连续的逗号,比如 “1,3” 。
注意:不允许重建树。
示例 1:
输入: preorder = “9,3,4,#,#,1,#,#,2,#,6,#,#”
输出: true
示例 2:
输入: preorder = “1,#”
输出: false
示例 3:
输入: preorder = “9,#,#,1”
输出: false
提示:
1 <= preorder.length <= 10……4^
preorder 由以逗号 “,” 分隔的 [0,100] 范围内的整数和 “#” 组成
题解:
方法:栈
class Solution {public boolean isValidSerialization(String preorder) {int n = preorder.length();int i = 0;Deque<Integer> stack = new LinkedList<Integer>();stack.push(1);while (i < n) {if (stack.isEmpty()) {return false;}if (preorder.charAt(i) == ',') {i++;} else if (preorder.charAt(i) == '#'){int top = stack.pop() - 1;if (top > 0) {stack.push(top);}i++;} else {// 读一个数字while (i < n && preorder.charAt(i) != ',') {i++;}int top = stack.pop() - 1;if (top > 0) {stack.push(top);}stack.push(2);}}return stack.isEmpty();}
}

下接:【题解】—— LeetCode一周小结14
——pytorch和torchvision安装)





![[C++面向对象]很难蒙混过关的CArray3d三维数组模板类](http://pic.xiahunao.cn/[C++面向对象]很难蒙混过关的CArray3d三维数组模板类)

——十分钟吃透vue路由router)
)
)


)

)



