1.什么是群(Group)?
对于一个集合 G 以及集合上的操作 ,如果G
G-> G,那么称(G,
)为一个群,并且满足如下性质:
- 封闭性:

- 结合性:

- 中性元素:

- 逆元素:

2.什么是阿贝尔群(Abelian group)?
满足交换(commutative)特征的群,称为阿贝尔群。
 3.(
3.(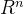 ,+)和(
,+)和(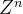 ,+)是阿贝尔群吗?说明理由。
,+)是阿贝尔群吗?说明理由。
- 满足封闭性:

- 满足结合性
- 中性元素是:
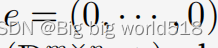
- 逆元素是:

- 满足交换性
4.(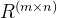 ,+)是阿贝尔群吗?
,+)是阿贝尔群吗?
是
5.什么是一般线性群(general linear group)?
讨论(,*)可逆/正则/非奇异方阵以及关于方阵的multiply的操作,是群,但是不是阿贝尔群,因为矩阵乘法不满足交换性。
- 封闭性和结合性同一般矩阵
- 中性元素:单位矩阵
- 逆元素:对于任意矩阵其逆元素是它的逆矩阵
6.什么是实数向量空间/线性空间(vector space)?
对于向量空间V=(V,+,*)拥有两种操作:
- +:V操作V得到V (是向量的add操作,每两个向量的逐个元素相加)
- *:实数R操作V得到V (是标量乘法scale操作,用向量乘以标量)
同时满足下列条件:
- (V,+)是一个阿贝尔群
- 分配性:

- 结合性:

- 中性元素:1(对于*,因为+是阿贝尔群)
7.举例一些常见的线性空间?
- n维向量空间

- m行n列矩阵

- 复数域可以看做是实数域上的线性空间

8.什么是向量子空间(Vector Subspace)?
如果向量空间,并且
,并且U也是满足add和scale的向量空间。
例如齐次线性方程组![]() 的解
的解是Rn的向量子空间,但是非齐次线性方程组
![]() 的解就不是Rn的子空间。任何一个Rn的子空间都是齐次线性方程组的解。
的解就不是Rn的子空间。任何一个Rn的子空间都是齐次线性方程组的解。
9.什么是线性组合(Linear Combination)?
首先考虑向量空间V,,
,有
 称
称是向量
的线性组合。
10.什么是线性无关(Linear Independent)?
考虑一个向量空间V,其中![]() ,如果存在线性组合满足
,如果存在线性组合满足![]() ,其中至少一个λ!=0,那么说明
,其中至少一个λ!=0,那么说明线性相关(Linear dependent),但是如果仅仅存在所有
,那么说明
线性无关(Linear Independent)。
11.寻找线性无关向量的方法?
- 首先要确定的是k个向量要么线性无关,要么线性相关,不可能存在第三种情况
- 如果至少一个向量
是0向量,那么他们一定线性相关。如果两个向量,并且他们相同,那么也一定线性相关。
- 如果其中一个向量xi是另一个向量xj的倍数,或者其中一个向量x可以由其他向量线性表示
- 使用高斯消元法对
进行消元,初等变换成列向量之后,如果所有列向量都是pivot column,那么这k个线性无关,如果存在至少一个non-pivot column,那么说明这k个列向量线性相关。
12.如果m>k,那么x1,...,xm线性相关



寄存器及汇编mul、div指令)

-- url,tcp,udp,socket)





)




考虑分布式电源不确定性的配电网鲁棒动态重构)



