前言

        我们都知道在HashMap中，当数组长度大于64并且链表长度大于8时，HashMap会从数组+链表的结构转换成红黑树，那为什么要转换成红黑树呢，或者为什么不一开始就使用红黑树呢？接下来我们将去具体的去剖析一下！

一、首先介绍一下红黑树？

        红黑树是一种自平衡的二叉搜索树，它是一种在插入和删除操作时能够自我调整以保持平衡的数据结构。红黑树之所以称为红黑树，是因为每个节点都具有颜色属性，可以是红色或黑色，这些颜色属性必须满足一定的约束条件，以确保树的平衡性。

红黑树必须满足四个条件！

1. 根节点是黑色的。
2. 每个叶子节点（NIL节点，即空节点）是黑色的。
3. 如果一个节点是红色的，则它的两个子节点都是黑色的（不能有连续的红色节点）。
4. 从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点（黑色节点的数量被称为该节点的“黑色高度”）。

然后它在插入和删除具体是怎么实现的，相对来说过程会比较复杂，简单概括以下步骤：

1. 刚插入的节点，默认是红色节点，它会一次次进行比较，比当前节点小就放在左边，比当前节点大就放在右边，也就是二分查找，所以复杂度是O(log n)；
2. 那接下来就是要满足上面的四个条件了，大概实现就是会在爷叔父节点之间进行一个红黑颜色互换，或者说在自旋之后再进行颜色互换，以满足上述四个条件。

当然，想了解红黑树插入和删除具体是怎么实现的，可以看这个视频，讲的很清晰：https://www.bilibili.com/video/BV18C4y137jn?vd_source=b16ef7f0a66010623908ff61e2645909

二、HashMap为什么使用红黑树代替数组+链表？

在说这个问题之前，先说一下数组、链表和红黑树各自的一个特点

1、数组

• 查询快：数组支持通过索引进行 O(1) 时间复杂度的一个随机访问，这意味着可以直接访问任何位置的元素。并且数组在内存中是连续存储的，这种紧凑的布局有利于 CPU 缓存的命中率，提高访问效率；
• 增删慢：在数组中插入元素需要将插入位置后面的所有元素向后移动一个位置，以便为新元素腾出空间，这涉及到大量元素的移动，尤其是在数组的开头或中间插入元素时。 类似地，从数组中删除元素时，需要将删除位置后面的所有元素向前移动一个位置，以填补删除元素留下的空隙。所以当对最后一个元素进行增删时，复杂度是O(1)，对其它元素进行增删时，复杂度是O(n)；
• 需要预先分配内存：数组在使用前需要预先分配内存空间，其大小通常是固定的。

2、链表

• 查询慢：链表查找元素需要从头节点开始按顺序遍历到目标位置，时间复杂度为 O(n)。并且，链表中的节点在内存中是分散存储的，这可能导致缓存不命中，从而降低访问效率。
• 增删快：链表的插入和删除操作具有 O(1) 的时间复杂度，无论是在链表的头部、尾部还是中间插入或删除元素，都只需要修改相邻节点的指针，而不需要移动其他元素。
• 无需预先分配内存： 链表不需要预先分配连续的内存空间，每个节点可以在需要时动态分配，这意味着链表可以轻松地扩展或收缩，不会浪费内存。

3、红黑树

• 查询，增删都比较快：因为它是一种二分查找树，它的查询、增删的时间复杂度都为O(log n)，虽然它的查询速度比不过数组，修改速度比不过链表，但是在大量的数据下，红黑树非常的稳定，它的修改效率远远大于数组，查询效率远远大于链表；
• 有序性： 红黑树是一种有序的数据结构，可以轻松实现范围查询、有序遍历等操作。
• 动态性能好： 红黑树能够适应动态数据的变化，保持较为稳定的性能表现。

那其实答案也是很明显了，也就是在HashMap存了大量的数据情况下，数组的查询效率可以，但是增删效率太慢了，链表的增删效率可以，但是查询效率太慢了，而红黑树刚好是个折中的选择，它的增删改查效率都很不错，都是O(log n)。

那为什么是数组长度大于64并且链表长度大于8才转换成红黑树？为什么不一开始就使用红黑树呢？

我们来看看HashMap源码注释是怎么说的：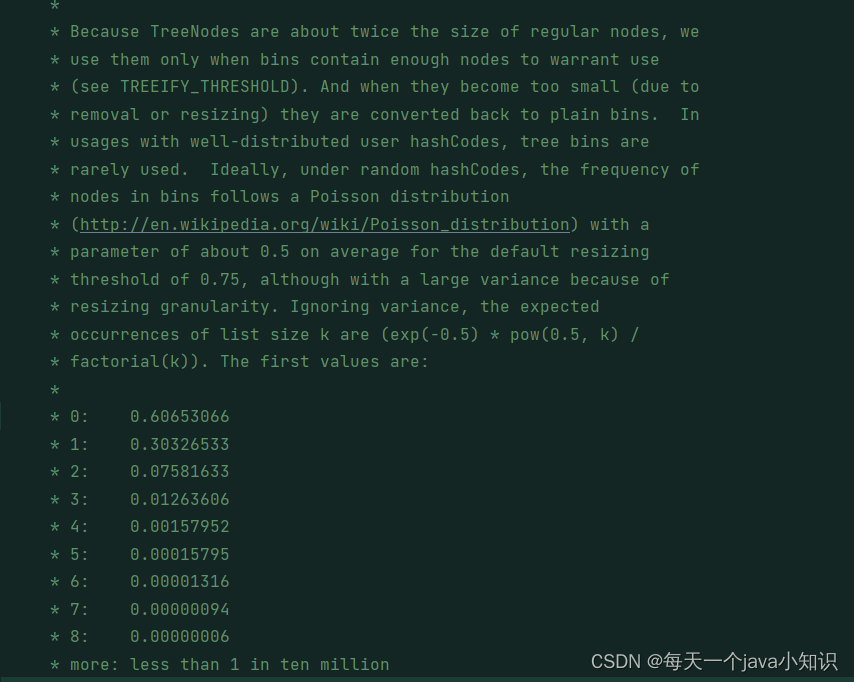

        大概意思就是说，因为树节点所占的空间是普通节点的两倍，所以我们只有在桶中包含足够的普通节点时才使用树节点。

        而为什么阈值是8，这涉及到一个泊松分布的概念，在理想情况下，桶(bins)中链表长度的值符合泊松分布，当链表长度为 8 的时候，概率仅为 0.00000006。 所以在理论上来说，当存入1666万数据的时候，链表长度才会达到8。

        从平均查找长度来看，红黑树复杂度是O(log n)，它的平均查找长度是log n，如果长度为8，则log n=3；而链表的复杂度为O(n)，最好的情况为1次，最坏的情况为n次，平均查找长度为n/2，长度为8时，n/2=4，所以阈值8时，红黑树的检索效率要大于链表。

        当长度为6时红黑树退化为链表，是因为log n=log 6约等于2.6，而n/2=6/2=3，两者相差不大，而红黑树节点占用的内存空间是普通节点的两倍，所以此时转换最合适。

三、总结

为什么不一开始就使用红黑树？

1. 在数组长度和链表长度不大的时候，数组+链表的性能也很好；
2. 而红黑树插入元素时，需要保证满足红黑树的四个特性，那它红黑颜色替换，或者自旋后替换，需要消耗一定的性能；
3. 并且树节点所占的空间是普通节点的两倍，那它需要占用更多的内存空间。
4. 一句话就是，小而美，迫不得已才用红黑树，杀鸡焉用牛刀！

那为什么是当数组长度大于64并且链表长度大于8时，才转换成红黑树？

1. 在理想情况下，桶(bins)中链表长度的值符合泊松分布，当链表长度为 8 的时候，概率仅为 0.00000006。 在理论上来说，当存入1666万数据的时候，链表长度才会达到8。
2. 而通常我们的 Map 里面是不会存储这么多的数据的，所以通常情况下，并不会发生从链表向红黑树的转换。
3. 所以我们平时基本见不到转换成红黑树的场景，但是假如你重写hashCode()方法进行恶搞，让它每次都是固定值，那他就会发生hash碰撞，每次碰撞都会加入链表尾部，当链表长度大于8时，很可能就转换成红黑树了。这点可以注意一下，hashCode()请不要设置固定值，不然很容易树化，到时候内存占用会增加一倍！

ps：以下是我整理的java面试资料，感兴趣的可以看看。最后，创作不易，觉得写得不错的可以点点关注！

链接：https://www.yuque.com/u39298356/uu4hxh?# 《Java知识宝典》