切比雪夫距离(Chebyshev distance)

切比雪夫距离是指在几何空间中两点之间的最大差值，或者说是两点在各个坐标轴上差值的最大绝对值。它以数学家彼得·切比雪夫（Peter Chebyshev）的名字命名。

在二维空间中，切比雪夫距离可以表示为两点在横纵坐标上差值的最大绝对值；在三维空间中，则是在三个坐标轴上的差值的最大绝对值。以此类推，切比雪夫距离可以适用于任意维度的空间。

切比雪夫距离可以用于衡量两个向量或数据集之间的相似性或距离。它常用于聚类分析、图像处理以及机器学习算法中的分类与聚类任务，特别适用于具有不同量纲或规模的数据集。与曼哈顿距离相比，切比雪夫距离更关注各个坐标轴上的最大差异，而不考虑中间的差异。

距离公式:

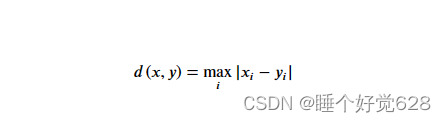
编写代码：

##### 在此处编写或补全代码
def ChebyshevDistance(x, y):import numpy as np

计算
a = np.array((2,3))
b = np.array((10,5))
##### 在此处编写或补全代码
dist4= np.max(np.abs(a-b))
print(f"d4={dist4}\n")

计算结果：