最优化模型的概述：

从某种程度上说，我们的世界是由最优化问题组成的。每一天，我们的生活都面临无数的最优化问题：上班怎么选择乘车路线，才能舒服又快速地到达公司；旅游如何选择航班和宾馆，既省钱又能玩地开心；跳槽应该选择哪家公司，钱多、事少、离家近；买房子应该选在哪里，交通发达有学区，生活便利升值快。

可以看出，上面所有的问题都面临无数的选择，我们会根据自己的偏好对每个选择打一个不同的分数，再从所有的选择中找出最优的一个。这个寻求最优解的过程其实就是最优化问题，我们要打的分数就称为目标函数。

最优化方法是机器学习中模型训练的基础，机器学习的很大一部分内容就是通过最优化方法找到最合适的参数，使得模型的目标函数最优。

最优化问题的定义：

最优化问题的定义：

在给定的约束条件下，选择最优的参数和使得目标函数最大化/最小化。

最优化问题的三个基本要素：     

目标函数：用来衡量结果的好坏     

参数值：未知的因子且需要通过数据来确定     

约束条件：需要满足的限制条件

Note: 目标函数必须是凸函数，才能保证优化后获得的最优结果是全局最优而不是局部最优，否则要进行凸优化。

凸函数：

简单理解为在函数图像上任取两点，如果函数图像在这两点之间的部分总在连接着两点的线段上方，则为凸函数。

凹函数：

简单理解为在函数图像上任取两点，如果函数图像在这两点之间的部分总在连接这两点的线段的下方，则为凹函数。

最优化模型的分类：

最优化模型分类方法有很多，可按变量、约束条件、目标函数个数、目标函数和约束条件的是否线性，是否依赖时间等分类。

根据约束条件来分类。首先最优化问题通常是带约束条件，比如对旅行路线的选择，总花费和出发、到达时间就构成了约束条件；对买房子的选择，离公司的路程、总价也可能构成约束条件。我们选择的最优解也必须满足这些约束条件。

最优化问题根据约束条件的不同主要分为三类：

   无约束优化

   等式约束的优化

   不等式约束的优化

无约束优化问题：

无约束最优化的求解方法主要有解析法和直接法。

无约束优化常表示为：

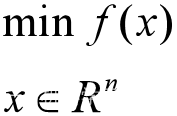
直接方法为费马定理(Fermat), 即使用求取函数f(x)的导数，然后令其为零， 可以求得候选最优值。再在这些候选值中验证，如果是凸函数，可以保证是最优解。

解析法,是根据无约束最优化问题的目标函数的解析表达式给出一种求最优解的方法，主要有梯度下降法，牛顿法等。

无约束优化的应用：

当下最常用的无约束优化方法为梯度下降法。在机器学习算法中应用到梯度下降方法进行优化的主要算法有：线性回归，逻辑回归，神经网络等。

梯度下降常用的方法有三种：

批量梯度下降(BGD)：每次更新使用所有的训练数据，最小化损失函数，如果只有一个极小值，那么批量梯度下降是考虑了训练集所有数据，是朝着最小值迭代方向运动的，但如果样本数量过多，更新速度会很慢。

随机梯度下降(SGD)：每次更新的时候只考虑了一个样本点，这样会大大加快训练数据，也恰好是BGD的缺点。但是有可能陷入局部最优，不一定是朝着极小值方向更新，且SGD对噪声也更加敏感。

小批量梯度下降(MBGD)：MBGD解决了批量梯度下降法的训练速度慢问题，以及随机梯度下降法的准确对噪声敏感的问题。

https://www.zhihu.com/question/36301367 梯度下降

等式约束的优化问题：

等式约束的优化问题，可以写为：

                                                   min f(x)

                                                   s.t. h_k(x)=0 k=1,2,…,k

上式中s.t. 指 “subject to”意思是“受限于”、“受某某约束”。 求f(x)的极小值，但x的取值必须满足k个h(x)等式。自变量x被限定在一个可行域内，在这个可行域内不一定存在着一个x令f(x)的导数或梯度等于0。

主要的解决方法：

消元法 ：将许多关系式中的若干个元素通过有限次的变换，消去其中的某些元素。例如：带入消元，加减消元等

拉格朗日乘子法：首先要求解的是最小化的问题，所以如果能够构造一个函数，使得该函数在可行解区域内与原目标函数完全一致，而在可行解区域外的数值非常大，那么这个没有约束条件的新目标函数的优化问题就是原来约束条件的原始目标函数的优化问题是等价的问题。使用拉格朗日方程的目的：将约束条件放到目标函数中，从而将有约束优化问题转换为无约束优化问题。

带约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数：

 其中λ_k是各个约束条件的待定系数（拉格朗日乘子）且λ_k大于等于0，是我们构造新目标函数是引入的系数变量。

拉格朗日乘子法常常会结合拉格朗日对偶法将不易求解的优化问题转化为易求解的优化。

【机器学习6】python实现拉格朗日乘子法_pycharm实现拉格朗日乘子法-CSDN博客

不等式约束的优化问题:

对于不等式约束的优化，可以写为：

主要通过KKT条件(Karush-Kuhn-Tucker Condition)将其转化成无约束优化问题求解。 

KKT三条件：

条件1：拉格朗日乘子(λ)求导为0的条件

条件2：h_j (x)=0,(j=1,2,…,m)

条件3： λ g_i(x)=0,(i=1,2,…,m)，λ≥0

https://www.sohu.com/a/196838208_99916544  KKT条件举例

 小结：

最优化问题	无约束	直接法	求导，导数等于0
		梯度下降	随机梯度下降
			批量梯度下降
			小批量梯度下降
	等式约束	消元法
		拉格朗日乘子法
	不等式约束	KKT（必须是凸函数）