C++AVL树拓展之红黑树原理及源码模拟

前言：我们之前已经从零开始掌握AVL树http://t.csdnimg.cn/LaVCChttp://t.csdnimg.cn/LaVCC

现在我们将继续学习红黑树的原理并且实现插入等功能，学习本章的前提要求是掌握排序二叉树和AVL树，本章不再提及一些基础知识，防止本文结构臃肿，对二叉排序树和AVL树有兴趣的可以阅读上面链接的文章，很多人可能说既生瑜何生亮，有了AVL树为什么还要红黑树，当然是因为红黑树的效率更高啦，AVL树的平黑太过于依赖平衡因子，稍微不平衡就会旋转，而大量的旋转自然降低了效率，红黑树相对AVL树没有那么平衡，旋转次数也少了，但是查询效率略微的降低就减少了不少的旋转，何乐而不为呢？更何况C++是一门以高效出名的语言。

一，红黑树的基本准则

二，红黑树为什么是平衡的

三，代码实现

1）敲前准备

2）查找

3）插入

4）迭代器

一，红黑树的基本准则

希望大家先记住红黑树本质还是一颗二叉排序树。在二叉排序树的基础上，AVL树是加了平衡因子，来保持树的结构平衡，红黑树则是通过给每个结点标记颜色达到相对平衡。（为什么要平衡是为了提高查询效率，不懂看链接博客）

1）每个结点的颜色不是黑色就是红色

2）红黑树根节点的颜色是黑色的（这条规定会在后面平衡的调整那里给出原因，现在记住即可）

3）红黑树上不能出现两个相邻的红色结点（红黑树平衡的重要准则）

4）每个叶子结点都是黑色的。（注意这里的叶子结点指的是NULL结点）

5）每条路径上的黑色结点的数目都是一样多的

6）最短路径小于最长路径的两倍（这个其实不是原则，是一个推论，下面会讲解，不必纠结）

二，红黑树为什么是平衡的

接下来我们将讨论一下为什么红黑树是平衡的。

讨论这个性质我们要从上面说的红黑树的基本准则入手。红黑树不过三种情况我们分类讨论

1）结点的颜色全是黑色

如果红黑树的结点颜色全是黑色，那么这棵树必定是一个完全二叉树，因为如果不是完全二叉树，红黑树的结点有全是黑色，那就违背了上面的第五条原则（每条路径上的黑色结点的数目都是一样多的）。

得出来红黑树的结点全是黑色的则次数必定平衡。

2）除了根节点其他结点都是红色

这种情况只有四种情况，我直接给大家画出来，记住不能违背上面的第三个准则（红黑树上不能出现两个相邻的红色结点）。

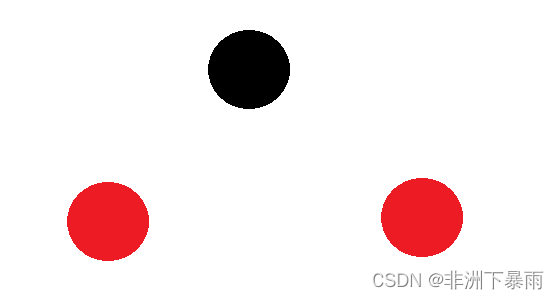
如果再插入结点必然出现黑色结点，不满足我们这种情况了。

3）既有红色结点也有黑色结点

首先根据上面的准则，每条路径上的黑色结点数目一样，红色结点不能相邻出现，也就是两个红色结点之间必然有若干个黑色结点，然而每条路径上黑色结点的数目已经固定了，我们现在看极端情况，也就是最短的路径一个红色结点也没有，最长的路径上每个红色结点之间只有一个黑色结点。

从上面的图可以得到最长路径绝对不会超过最短路径的两倍，因为红色结点的数目不会超过黑色结点，当然上面是把路径单独列出来了来，实际上是树状结构。

综上所述红黑树的是一个相对平衡的二叉树。

三，代码实现

1）敲前准备

首先我们需要一个标记位来记录当前结点的颜色，我们采用枚举类型，可读性强

enum color {red,black
};

结点里面的内容应该包括什么呢？data存储数据，三个指针，一个parent指针，一个leftchild和rightchild指针，结构体里面应该包括我们刚刚的枚举。

template<class T>
struct RBTreeNode {RBTreeNode(T data) {_pParent = NULL;_pLeft = NULL;_pRight = NULL;_data = data;c = red;}RBTreeNode() {_pParent = NULL;_pLeft = NULL;_pRight = NULL;c = red;}color c;RBTreeNode* _pParent;RBTreeNode* _pLeft;RBTreeNode* _pRight;T _data;
};

那么大致框架就搭起来了

enum color {red,black
};
template<class T>
struct RBTreeNode {RBTreeNode(T data) {_pParent = NULL;_pLeft = NULL;_pRight = NULL;_data = data;c = red;}RBTreeNode() {_pParent = NULL;_pLeft = NULL;_pRight = NULL;c = red;}color c;RBTreeNode* _pParent;RBTreeNode* _pLeft;RBTreeNode* _pRight;T _data;
};
template<class T>
class RBTree
{
private:Node* _pHead; //哨兵位size_t _size;//结点个数
};

2）查找

查找还是一个老套路，大于当前结点找右边，小于当前结点找左边，直到找到或者为空，属实是老生常谈了，这里不过多介绍。

// 检测红黑树中是否存在值为data的节点，存在返回该节点的地址，否则返回nullptrNode* _Find(const T& data) {Node* cur = _pHead->_pParent;//从根节点开始while (cur&&cur!=_pHead) {if (data < cur->_data)  //小于找左边cur = cur->_pLeft;else if (data > cur->_data) {   //大于找右边cur = cur->_pRight;}elsereturn cur;   //找到返回}return NULL;  //找不到}

3）插入

插入的第一件事就是找到应该插入的位置，这个简单，这个逻辑和查找一样。插入之后的颜色应该是红色还是黑色值得商榷，但仔细考虑，如果插入黑色的话就违背了每条路径上的黑色结点个数相等的原则，插入红色则可能碰到连续的红色结点，那到底是插入红色还是黑色呢？我们现在来讨论一下。

如果插入黑色结点的话，那么完全是牵一发而动全身，因为根据结点规则每条路径上的黑色结点的数目都是一样多的，我们需要把所有路径的黑色结点数目全部增加一个，这显然不是一个明智之举。那我们只剩下一个选择了，插入的新结点默认为红色结点，接下来我们需要分情况讨论。

1）插入结点的父亲结点是黑色，如果是黑色插入红色节点不需要改变任何结点，因为完全满足红黑树的规则，既没有连续的红色结点，每条路径的黑色结点数也都相同。

2）如果是父亲是红色的结点呢？

注：圆形代表一个结点，长方形代表很多种可能

这种情况我们需要看parent的兄弟结点的颜色了，接下来又要分情况讨论

1）兄弟节点是红色，这种情况我们把两个兄弟节点全变成黑色，把爷爷结点变成红色，然后继续递归往上，往上有两种可能，一种是一直递归到根节点，然后根节点变成红色，最后我们强制把根节点变成黑色就行了，并不会违背任何原则。当然可能中途兄弟节点是黑色，这个时候我们需要使用下面情况2的旋转来弥补了。

2）兄弟节点是黑色的时候，证明单纯靠变色已经无法将这颗红黑树拉上正途了，我们不得已采取暴力手段旋转了，旋转结果仍然需要遵守红黑树原则。这里面又分为好几种情况

旋转具体详细过程，参考我的往期博客

http://t.csdnimg.cn/a13umhttp://t.csdnimg.cn/a13um

1）左旋（之所以每个节点下面都可能有节点是因为，新插入的节点不可能碰到这种情况，只可能是情况1向上递归解决的时候出现的）

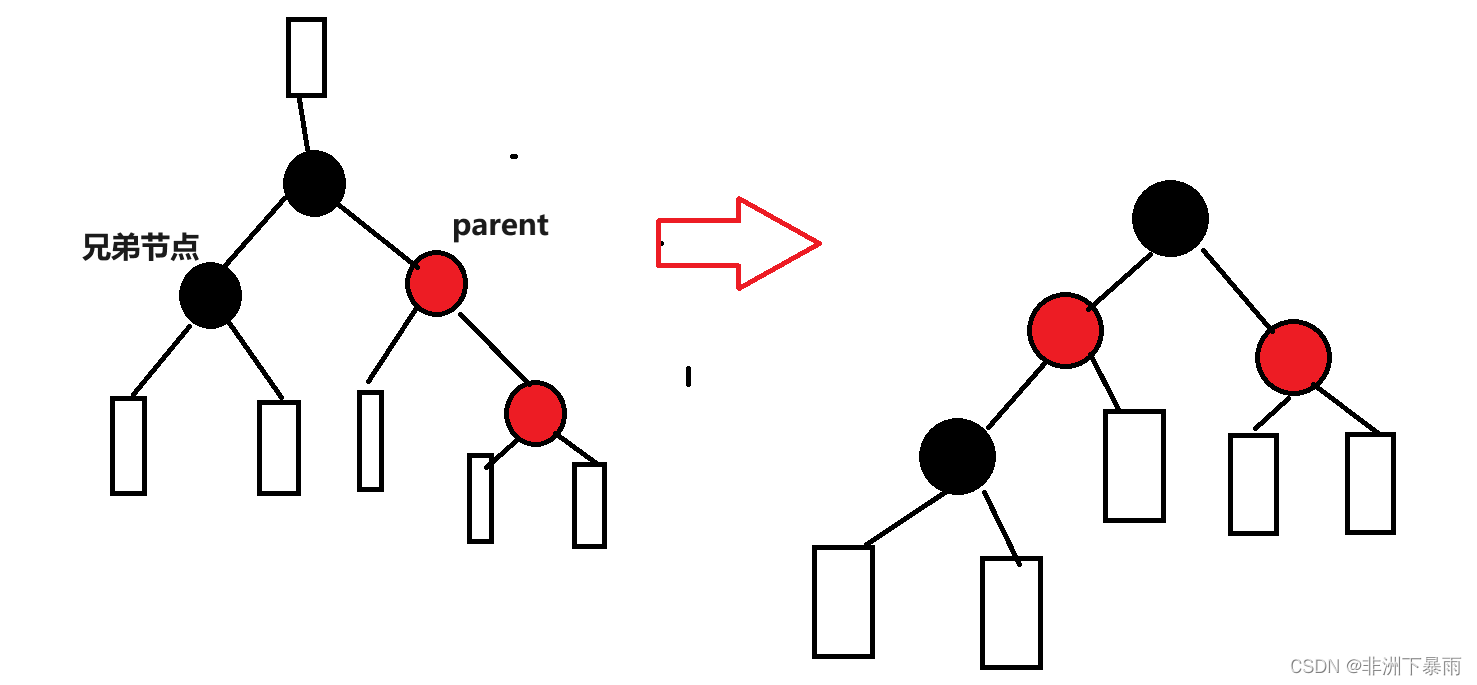
void RotateL(Node* pParent){Node* pSubR = pParent->_pRight;Node* pSubRL = pSubR->_pLeft;pParent->_pRight = pSubRL; //防止访问空结点if (pSubRL)pSubRL->_pParent = pParent;pSubR->_pLeft = pParent;Node* pPParent = pParent->_pParent;pSubR->_pParent = pPParent;pParent->_pParent = pSubR;if (pPParent == _pHead)     //根节点单独处理_pHead->_pParent = pSubR;else{if (pParent == pPParent->_pLeft)pPParent->_pLeft = pSubR;elsepPParent->_pRight = pSubR;}}

2）右旋

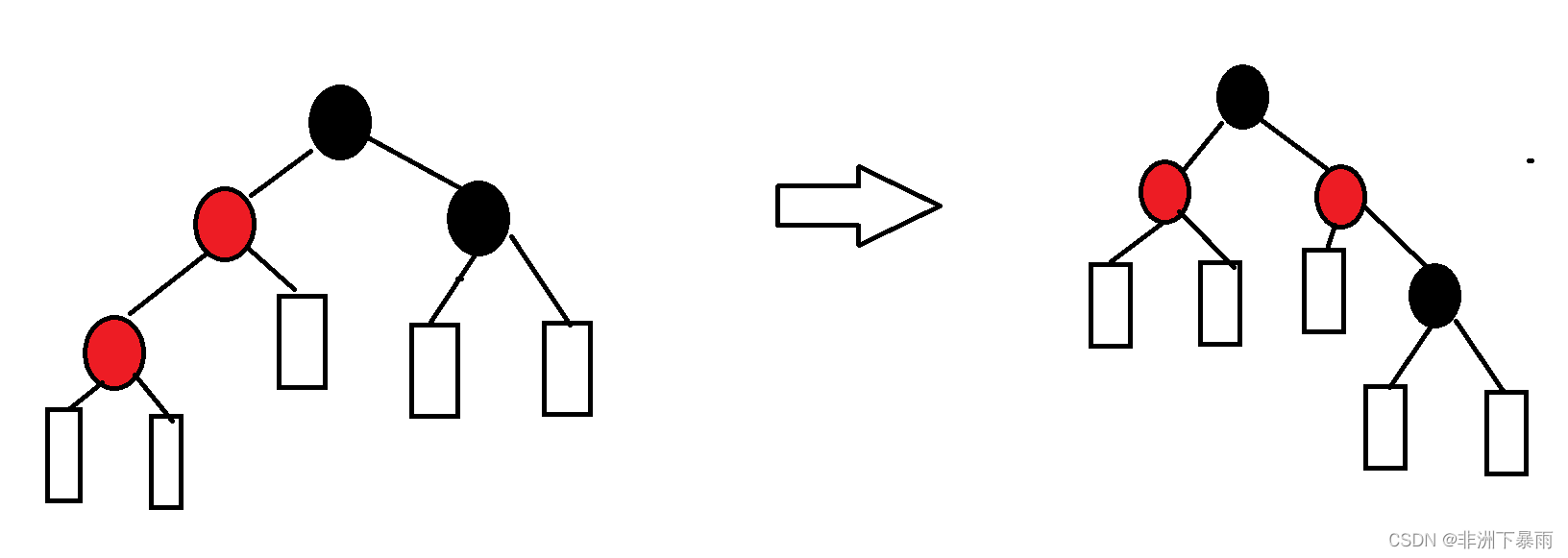
void RotateR(Node* pParent){Node* pSubL = pParent->_pLeft;Node* pSubLR = pSubL->_pRight;pParent->_pLeft = pSubLR;if (pSubLR)       //防止访问空结点pSubLR->_pParent = pParent;pSubL->_pRight = pParent;Node* pPParent = pParent->_pParent;pParent->_pParent = pSubL;pSubL->_pParent = pPParent;if (pPParent == _pHead)      //根节点单独处理_pHead->_pParent = pSubL;else{if (pParent == pPParent->_pLeft)pPParent->_pLeft = pSubL;elsepPParent->_pRight = pSubL;}}

3）右旋加左旋

4）左旋加右旋

双旋代码复用单旋就行了

插入代码：

bool _Insert(const T& data) {if (_Find(data)) {cout << "元素已经存在" << endl;return false;}//插入第一个元素的时候if (_pHead->_pParent == _pHead) {Node* root = new Node(data);root->c = black;root->_pParent = _pHead;_pHead->_pParent = root;_pHead->_pLeft = root;_pHead->_pLeft = root;return 1;}Node* cur = _pHead->_pParent;Node* parent=cur;//找该插入的位置while (cur&&cur!=_pHead) {parent = cur;if (cur->_data > data) {cur = cur->_pLeft;}else if (cur->_data < data) {cur = cur->_pRight;}else {cout << "值：" << data << "已经存在" << endl;return 0;}}//插入cur = new Node(data);if (parent->_data > data) {parent->_pLeft = cur;cur->_pParent = parent;}else {parent->_pRight = cur;cur->_pParent = parent;}//调整Node* gparent = parent->_pParent;Node* uncle = _pHead;while (gparent&&parent->c != black) {if (gparent->_pLeft == parent) {uncle = gparent->_pRight;}else {uncle = gparent->_pLeft;}if (!uncle || uncle->c == black)break;else {uncle->c = black;gparent->c = red;parent->c = black;}cur = gparent;;parent = cur->_pParent;gparent = parent->_pParent;}if (cur == parent->_pLeft && parent == gparent->_pLeft && (uncle == NULL || uncle->c == black)) {RRotate(gparent); //左旋情况parent->c = black;gparent->c = red;}if (cur == parent->_pRight && parent == gparent->_pRight && (uncle == NULL || uncle->c == black)) {LRotate(gparent);  //右旋情况parent->c = black;gparent->c = red;}if (cur == parent->_pLeft && parent == gparent->_pRight && (uncle == NULL || uncle->c == black)) {RRotate(parent); //右左双旋LRotate(gparent);cur->c = black;gparent->c = red;}if (cur == parent->_pRight&& parent == gparent->_pLeft && (uncle == NULL || uncle->c == black)) {LRotate(parent);  //左右双旋RRotate(gparent);cur->c = black;gparent->c = red;}_pHead->_pLeft = LeftMost();_pHead->_pRight = RightMost();RightMost()->_pRight = _pHead;_pHead->_pParent->c = black;_size++;return 1;}

4）迭代器

迭代器属于老生常谈了，就是运算符重载，我们这里不做过多讲解，但是我们这里面有两个难点，就是++，--拿的是哪个结点？

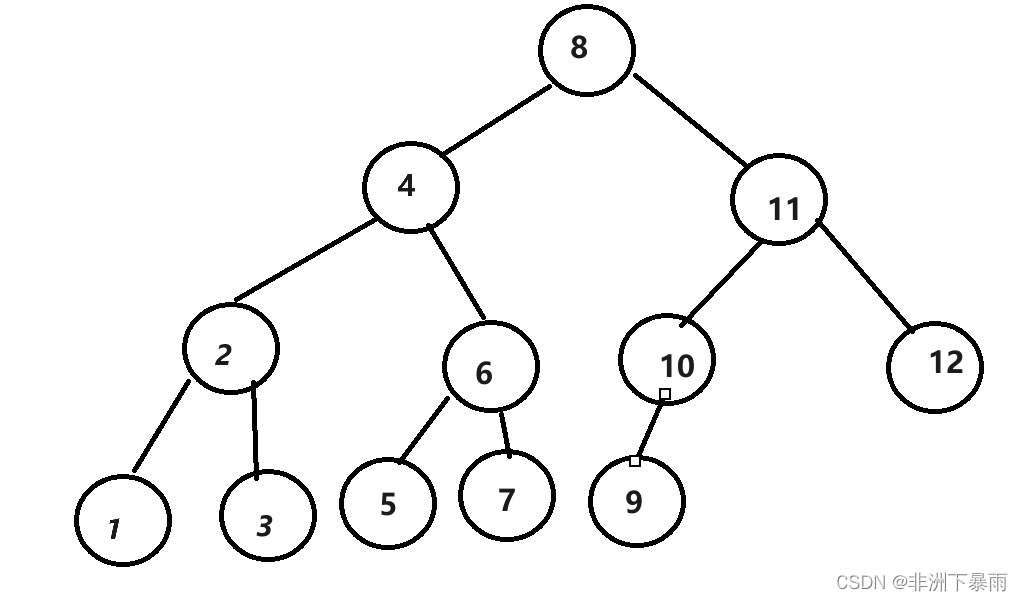
首先看4的下一个下一个结点是什么（也就是++）？如果右子树不为空的话，下一个结点是右子树的最左结点。

那7的下一个结点是什么呢？当右子树为空时，一直递归向上直到这个这颗子树是某个结点的左孩子，这个结点就是下一个结点。

struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef typename RBTreeIterator<T> Self;
public:
Self& operator++() {if (_pNode->_pRight != NULL) //右子树不为空的情况下{_pNode = _pNode->_pRight;if (_pNode->_pParent->_pParent == _pNode) {RBTreeIterator<T> ret(_pNode);return ret;}while (_pNode->_pLeft != NULL)_pNode = _pNode->_pLeft;RBTreeIterator<T> ret(_pNode);return ret;}while (_pNode != _pNode->_pLeft) {       //一直递归向上直到这个这颗子树是某个结点的左孩子if (_pNode->_pParent->_pParent == _pNode) {RBTreeIterator<T> ret(NULL);return ret;}_pNode = _pNode->_pParent;}RBTreeIterator<T> ret(_pNode->_pParent);return ret;}
};

那--呢？也就是上一个结点。例如4，当左孩子不为空时，左子树的最右结点就是你的上一个结点。

如果最子树为空呢？例如5，那就一直向上递归，直到这颗子树是某个结点的右孩子，这个结点就是上一个结点。

struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef typename RBTreeIterator<T> Self;
public:	
Self& operator--() {if (_pNode->_pLeft != NULL) { //左子树为空的情况_pNode = _pNode->_pLeft;while (_pNode->_pRight) {_pNode = _pNode->_pRight;}Self a(_pNode);return a;}else {   //一直向上递归，直到这颗子树是某个结点的右孩子while (_pNode->_pParent->_pRight != _pNode) {if (_pNode->_pParent->_pParent == _pNode) {RBTreeIterator<T> ret(NULL);return ret;}_pNode = _pNode->_pParent;}Self a(_pNode->_pParent);return a;}}
};

其他的运算符重载没啥难度，大家完全可以靠自己敲出来。

这篇博客花了作者大量心思，希望大家你点赞+收藏+转发。如果博客有不对的地方，可以评论区讨论。