参考链接：数据结构：图(Graph)【详解】_图数据结构-CSDN博客
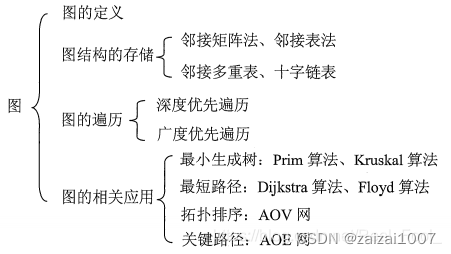
图的定义
图(Graph)是由顶点的有穷非空集合 V ( G ) 和顶点之间边的集合 E ( G ) 组成，通常表示为: G = ( V , E ) ，其中， G 表示个图， V 是图 G 中顶点的集合， E是图 G 中边的集合。 V={v1,v2,...,vn}，则用∣V∣表示图 G 中顶点的个数，也称图 G的阶，E={(u,v)∣u∈V,v∈V}，用 ∣E∣表示图 G中边的条数。
图不可以是空图，就是说不能一个顶点没有。图的顶点集V一定非空，边集可以为空，次是图中只有顶点没有边
图的基本概念和术语
有向图
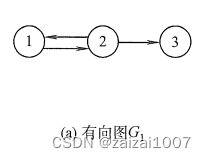
若E是有向边(也称弧)的有限集合时，则图G为有向图。弧是顶点的有序对，记为<v, w>，其中v,w是顶点，v称为弧尾，w称为弧头（被指向的称为头），<v,w>称为从顶点v到顶点w的弧，也称v邻接到w，或w邻接自v。
无向图
若E是无向边(简称边)的有限集合时，则图G为无向图。边是顶点的无序对，记为(v, w)或(w,v),因为(v,w)=(w,v), 其中v,w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v，或者说边(v, w)和顶点v, w相关联。
简单图
一个图满足 1.不存在重复边 2，不存在顶点到自身的边 则称为简单图
完全图（也称简单完全图）
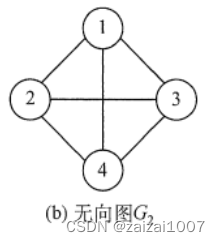
对于无向图，∣E∣的取值范围是 0 到n(n−1)/2，有n(n−1)/2条边的无向图称为完全图，在完全图中任意两个顶点之间都存在边。对于有向图，∣E∣的取值范围是0到n(n−1)， n(n−1)条弧的有向图称为有向完全图，在有向完全图中任意两个顶点之间都存在方向相反的两条弧。G2为无向完全图，而 G3为有向完全图。
子图
设有两个图 G=(V,E)和G′=(V′,E′)， 若 V′是 V的子集，且E′是E的子集，则称 G′是 G 的子图。若有满足V(G′)=V(G)的子图G′，则称其为G的生成子图。
注意：并非V和E的任何子集都能构成G的子图，因为这样的子集可能不是图，即E的子集中的某些边关联的顶点可能并不在V的子集中
连通，连通图和连通分量
在无向图中，若从顶点V到顶点w有路径存在，则称v和w是连通的。若图中G中任意两个顶点是连通的，则称图G是连通图，否则称为非连通图。无向图中的极大连通子图称为连通分量。若一个图有 n 个顶点，并且边数小于 n - 1，则此图必是非连通图
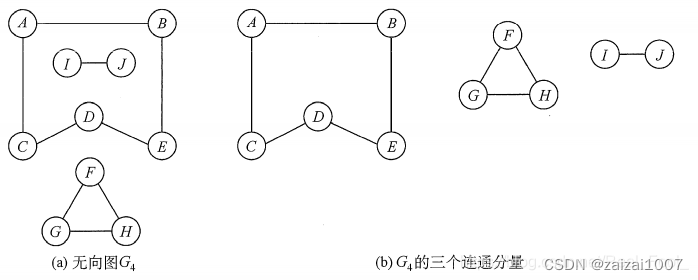
注意:弄清连通、连通图、连通分量的概念非常重要。首先要区分极大连通子图和极小连通子图，极大连通子图是无向图的连通分量，极大即要求该连通子图包含其所有的边;极小连通子图是既要保持图连通又要使得边数最少的子图。
强连通图 ，强连通分量
在有向图中，若从顶点 v 到顶点 w 和从顶点 w 到顶点 v 之间都有路径，则称这两个顶点是强连通的。若入中任何一对顶点都是强连通的，则称此图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量
强连通分量 -- >
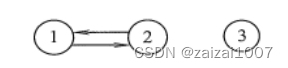
注意:强连通图、强连通分量只是针对有向图而言的。一般在无向图中讨论连通性，在有向图中考虑强连通性。
生成树，生成森林
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为 n,则它的生成树含有n−1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。在非连通图中，连通分量的生成树构成了非连通图的生成森林。图G2的一个生成树如下图所示。
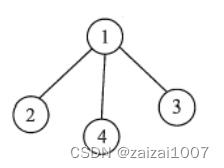
注意:包含无向图中全部顶点的极小连通子图，只有生成树满足条件，因为砍去生成树的任一条边，图将不再连通。
顶点的入度和出度
图中每个顶点的度定义为以该点为一个端点的边的数目
对于无向边，全部顶点的度的和等于边数的 2 倍，因为每条边和两个顶点相关联
对于有向图，顶点 v 的度分为 入度 和 出度 ，入度是以顶点 v 为终点的度，出度是以这个顶点为起点的度。在有向图中全部顶点入度和出度的和等于边数
边的权和网
在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值，这种边上带有权值的图称为带权图，也称为 网
