
🔥个人主页:努力学编程’
🔥内容管理:java数据结构

上一篇文章我们讲过了java数据结构的链表,对于链表我们使用了它的一些基本操作,完成了扑克牌小游戏的操作,如果你感兴趣的话,点击超链接观看:【java数据结构】基于java提供的ArrayList实现的扑克牌游戏-(附源码~),今天带大家学习的是数据结构中另一个非常重要的知识-栈
目录
- 1栈的一些基础知识
- java代码实现一个栈
- 对于栈功能的详解
- 1.压栈:
- 2.出栈pop:
- 3.获取栈顶元素peek:
- 逆波兰表达式求值:
- 中缀表达式:
- 后缀表达式:
- 那么如何实现中缀表达式和后缀表达式的转换:
- 解题思路:
- 代码实现
1栈的一些基础知识
在开始前,请牢记这句话:栈是一种先进后出的数据结构。栈(stack)是限定仅在表的一端进行操作的数据结构,请联系我们前文所学的,设想一个单链表我们只能够对其链表的表尾结点进行操作,而操作也只能够进行插入一个新的结点与删除最末尾的这个结点两个操作,而这样强限制性的‘链表’,就是我们所说的栈。
栈在底层逻辑的实现上可分为链表栈和数组栈:
栈分为数组栈和链表栈,其区别是数组栈使用数组进行功能的模拟,实现较为快速和便利,而链表栈使用链表的思路去设计,实现较为麻烦,但是其稳定不易出错;在链表栈中又分为静态链表栈和动态链表栈,静态链表栈给定栈的空间大小,不允许超过存储超过给定数据大小的元素,而动态栈使用的是自动创建空间的方法进行创建,只要符合机器的硬件要求以及编译器的控制,其理论上是极大的。
以下是实现一个栈的具体操作过程:
1.选择数据结构:
栈可以使用数组(或列表)或链表来实现。数组实现的栈通常更简单,因为它们具有随机访问的能力,而链表实现的栈可能需要更多的指针操作。
2.定义栈的操作:
定义栈的基本操作,包括入栈(push)、出栈(pop)、获取栈顶元素(peek)等。
3.确定栈的大小(如果有限制): 如果栈有大小限制,则需要确定栈的最大容量。如果栈的大小是动态的,则可以跳过此步骤。
4.实现栈的基本操作:
根据选择的数据结构,实现栈的基本操作。如果使用数组实现,通常使用数组的末尾作为栈的顶部,入栈操作将元素添加到数组末尾,出栈操作将从数组末尾移除元素。如果使用链表实现,需要定义节点类,并根据栈的操作更改节点的连接关系。
5.处理边界情况:
在实现栈的操作时,要考虑边界情况,如栈为空时尝试出栈或查看栈顶元素,或者栈已满时尝试入栈。
6.测试栈的实现:
编写测试代码,确保栈的实现能够正常工作,并处理各种情况,如入栈、出栈、查看栈顶元素、栈为空或栈已满等。
7.优化(如果需要):
根据实际需求和性能要求,可以对栈的实现进行优化,例如使用动态数组实现以处理栈大小动态变化的情况,或者使用链表实现以节省内存空间。
通过以上步骤,你可以实现一个简单而有效的栈数据结构。
java代码实现一个栈
import java.util.ArrayList;
import java.util.EmptyStackException;public class Stack {private ArrayList<Integer> stack;private int maxSize;// 构造函数public Stack(int maxSize) {this.maxSize = maxSize;this.stack = new ArrayList<>();}// 判断栈是否为空public boolean isEmpty() {return stack.isEmpty();}// 判断栈是否已满public boolean isFull() {return stack.size() == maxSize;}// 入栈操作public void push(int item) {if (isFull()) {System.out.println("Stack is full. Cannot push element.");} else {stack.add(item);}}// 出栈操作public int pop() {if (isEmpty()) {throw new EmptyStackException();}return stack.remove(stack.size() - 1);}// 获取栈顶元素但不移除public int peek() {if (isEmpty()) {throw new EmptyStackException();}return stack.get(stack.size() - 1);}// 获取栈的大小public int size() {return stack.size();}// 主函数用于测试public static void main(String[] args) {Stack stack = new Stack(5);// 入栈操作stack.push(1);stack.push(2);stack.push(3);stack.push(4);stack.push(5);// 获取栈的大小System.out.println("Stack size: " + stack.size());// 出栈操作System.out.println("Pop element: " + stack.pop());System.out.println("Pop element: " + stack.pop());// 获取栈顶元素System.out.println("Peek element: " + stack.peek());// 获取栈的大小System.out.println("Stack size: " + stack.size());}
}对于栈功能的详解
1.压栈:
向栈里插入数据,称为压栈,下面为图解:
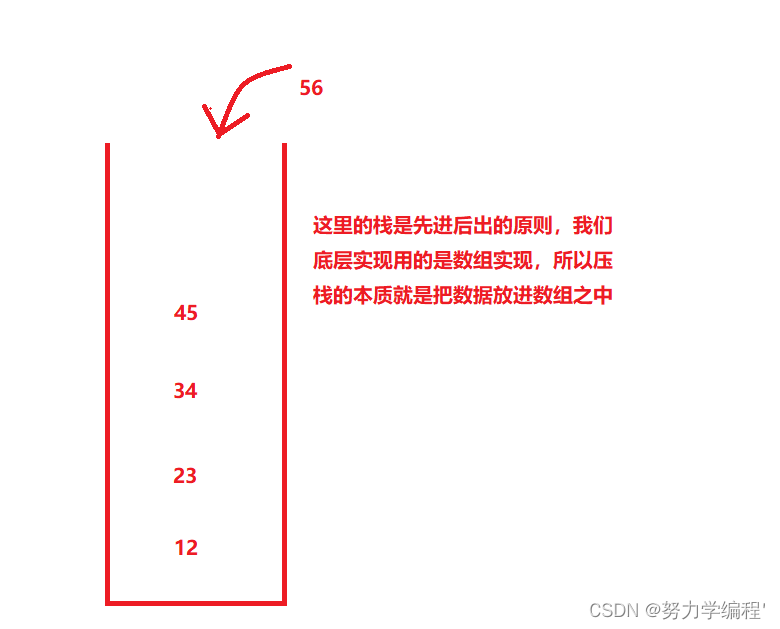
既然栈我们底层用的是数组实现,那么在我们压栈的时候,就必须考虑一件事情,数组是否已满,如果数组已经放满了,我们就必须先对数组进行扩容,然后才能对数据进行插入
那么具体应该如何对栈实现扩容呢,其实和数组扩容是一个道理:
public void push(int val){if(isFull()){Arrays.copyOf(elem,2*elem.length);}elem[usedSize]=val;usedSize++;}public boolean isFull(){return usedSize== elem.length;}
2.出栈pop:
将栈顶的元素弹出,后面的元素接替成为栈顶元素,属于栈的基本操作
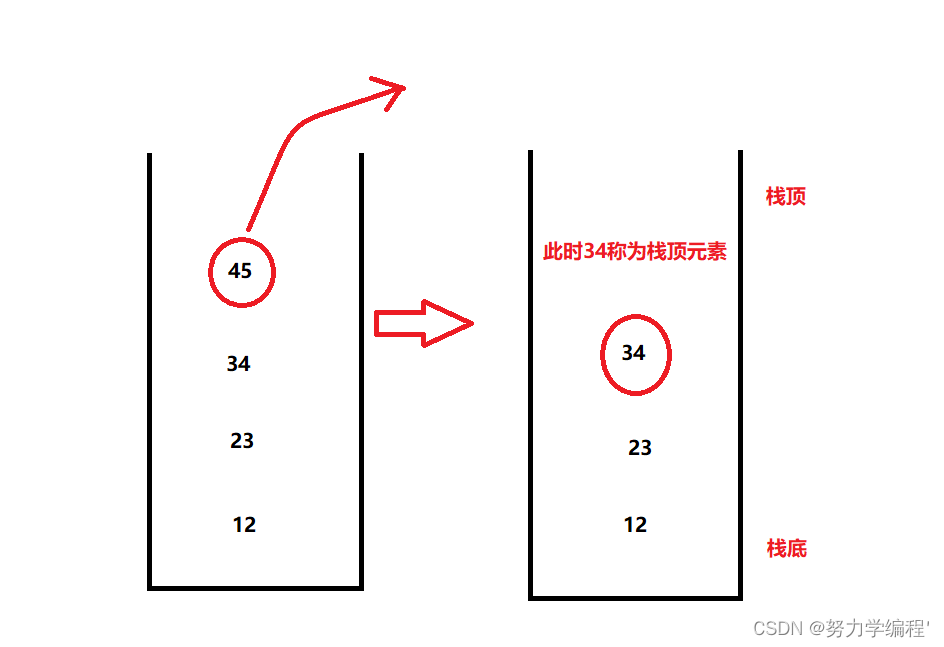
下面是使用java实现的pop方法:
public int pop(){if(empty()){return -1;}int oldVal=elem[usedSize-1];usedSize--;return oldVal;}public boolean empty(){return usedSize==0;}
将栈顶的元素返回,具体对于栈数据的删除,其实就是将usedSize–,代表将数组的大小进行了调整。
3.获取栈顶元素peek:
本质上其实就是将栈顶元素进行打印,需要注意的一点这个方法返回栈顶的元素但不移除它。
public int pop(){if(empty()){return -1;}int oldVal=elem[usedSize-1];usedSize--;return oldVal;}public boolean empty(){return usedSize==0;}public int peek(){if(empty()){return -1;}return elem[usedSize-1];}
}
以上就是对于栈的一些基本操作,了解完这些知识,我们就可以使用栈的知识解决一些算法题。
逆波兰表达式求值:
点击链接一起挑战,逆波兰表达式求值要想解决这道题,我们需要首先了解中缀表达式,后缀表达式的知识
中缀表达式:
中缀表达式是我们最常见的数学表达式形式,它采用操作符位于操作数之间的形式。例如,“3 + 4”、“(5 - 2) * 6” 等都是中缀表达式。
中缀表达式的特点包括:
1.操作符在操作数中间:例如,“3 + 4” 中的加号就位于操作数 3 和 4 之间。
2.使用括号:中缀表达式通常需要使用括号来明确运算的优先级和顺序。
3.常见的运算符优先级规则:乘除法优先于加减法,同级运算符按照从左到右的顺序计算。
后缀表达式:
后缀表达式,也称为逆波兰表达式(Reverse Polish Notation,RPN),是一种不需要括号来表示运算顺序的数学表达式形式。在后缀表达式中,操作符在操作数之后出现,因此不需要括号来明确运算的顺序。
后缀表达式的主要特点是:
1.没有括号:
不需要括号来指定运算次序,因为操作符始终跟在操作数之后。
2.明确运算顺序:
从左到右扫描表达式,每当遇到一个操作符,就从栈中弹出足够的操作数进行计算,然后将结果压回栈中,直到整个表达式扫描完毕。
3.简化计算:
后缀表达式减少了运算符的优先级问题,简化了计算过程。
例如,将中缀表达式 "3 + 4 * 5" 转换为后缀表达式为 "3 4 5 * +"。
处理后缀表达式的算法通常使用栈来实现。具体步骤如下:
1.从左到右遍历后缀表达式的每个字符。
2.如果遇到操作数,则将其压入栈中。
3.如果遇到操作符,则从栈中弹出相应数量的操作数进行运算,并将结果压入栈中。
4.最终栈中只剩下一个元素,即为后缀表达式的计算结果。
那么如何实现中缀表达式和后缀表达式的转换:
这里给大家分享一个方法:
1.首先将表达式严格改为中缀表达式
2.把每个运算符转移到对应括号的后面
3.完成后缀表达式的转化

解题思路:
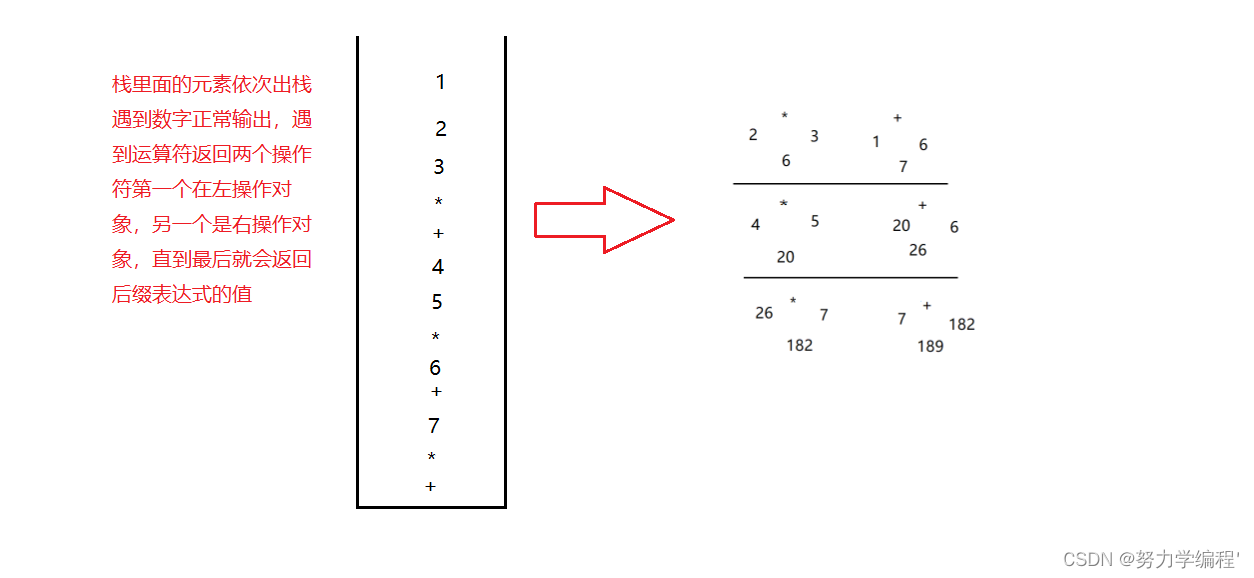
代码实现
public int evalRPN(String[] tokens) {int n = tokens.length;int[] stack = new int[(n + 1) / 2];int index = -1;for (int i = 0; i < n; i++) {String token = tokens[i];switch (token) {case "+":index--;stack[index] += stack[index + 1];break;case "-":index--;stack[index] -= stack[index + 1];break;case "*":index--;stack[index] *= stack[index + 1];break;case "/":index--;stack[index] /= stack[index + 1];break;default:index++;stack[index] = Integer.parseInt(token);}}return stack[index];}
好了,今天就分享到这里,谢谢大家!
)



)
![[TS面试]TS中使用Union Types时注意事项?](http://pic.xiahunao.cn/[TS面试]TS中使用Union Types时注意事项?)




等级考试三级考试真题2023年12月——持续更新.....)






之React探索)

