机器学习--支持向量机(通俗版本+demo)

场景

假设我们要在一个在线零售平台上自动区分商品评论是正面的还是负面的。评论中的语言多种多样，且往往含有大量的非结构化文本数据，直接使用简单的规则来分类是非常困难。这时候我们采取支持向量机算法来分类是一个比较好的选择。

支持向量机

支持向量机（SVM）是一种强大的监督学习算法，用于分类和回归分析。其核心思想是找到一个最优的超平面，以此来区分不同类别的数据点。SVM特别适合中小型复杂数据集的分类问题。

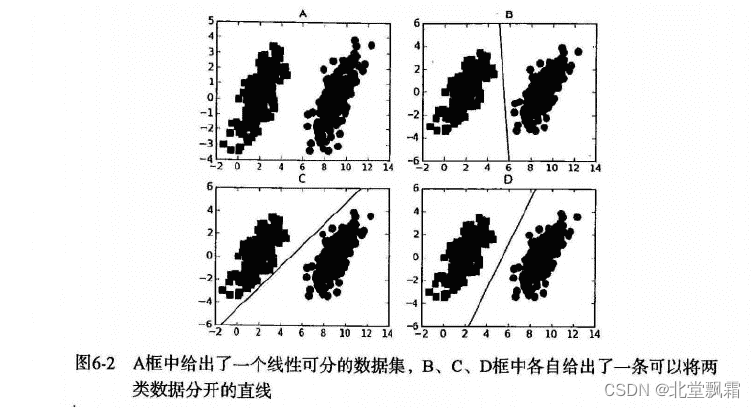
在这里插入图片描述
给左右的点使用一条直线划分，明显可以得出，第四个的效果明显比另外两条线好很多。

核心概念

支持向量机（SVM）的心脏部位——最优超平面和核技巧。

最优超平面

想象咱们是一群寻宝者，在宝藏岛上寻找金银财宝。岛上有两个洞穴，一个藏金币，一个藏银币。咱们的目标是用最少的线索找到一条线，能够把金币洞穴和银币洞穴分开。这条线，就是SVM中的最优超平面，它的特点是能最大程度上把两类宝藏分开，让咱们的分类任务清晰又精准。

核技巧神秘的地图

在海上航行，核函数就像是咱们的神秘地图，能揭示隐藏在平静海面下的秘密通道。通过使用不同的核函数，咱们可以发现数据之间复杂的关系，就像找到了通往宝藏的秘密通道。

线性核：这就像是直接向宝藏岛行驶，适用于宝藏就藏在不远的海岛上的情况。
多项式核：通过提升到高维空间，它可以帮助咱们在看似复杂的海域中找到通向宝藏的路径，适用于宝藏被隐藏得比较深的情况。
径向基（RBF）核，也就是高斯核：这是最强大的一张地图，它能揭示出最隐秘的通道，哪怕宝藏被隐藏在最复杂的地形之下。

惩罚因子 C：调节风帆

想象一下，咱们的船在大海上航行，惩罚因子 C 就像是调节风帆的绳索。如果咱们拉紧绳索（即提高 C 值），风帆会紧绷，船就会更精确地追随风向，尽可能不偏离航线，哪怕是小小的风浪（数据噪声）也想避开。但这样做的风险是，一旦遇到大风浪（过拟合），船可能就控制不住了。如果咱们放松绳索（即降低C 值），风帆会松弛，船虽然不会那么精确追随每一阵风，但在大风浪面前能更灵活地调整，保持航行（避免过拟合），哪怕航线上有点小偏差（允许一些错误分类）。

松弛变量 ξ：接纳乘客的弹性

想象咱们的船只在收容乘客。松弛变量 ξ 就好比是咱们对乘客（数据点）的容纳度。有些乘客可能不完全符合咱们的乘客标准（比如，穿着不整齐的），但为了整体的航行目标（比如，分类的正确性），咱们可以选择稍微放宽标准，容纳他们上船。通过调整松弛变量，咱们可以决定容纳这些不符合标准乘客的程度。但记住，每个不符合标准的乘客都需要支付额外的金币（惩罚），以确保他们尽量不影响航行的整体目标。

指标：航行的星辰

在咱们的航海中，性能指标就像是指引方向的星辰。它们告诉咱们航行的准确性、效率、以及咱们是否正朝着正确的方向前进。常见的指标包括准确率（咱们正确预测的比例）、召回率（在所有正样本中，咱们正确找到的比例），以及F1分数（准确率和召回率的调和平均，用来平衡两者的性能）。

最终目标

通过使用这些工具和参照这些指标，咱们就能在数据的大海中找到通往知识宝藏的路径。记住，选择正确的工具和正确解读指标，是达到目的地的关键！

手写图片识别工具

步骤概览

数据准备：加载图片数据，对数据进行预处理和标准化。
特征提取：将图片转换为适合机器学习模型处理的格式。
训练测试分割：将数据集分为训练集和测试集。
模型训练：使用SVM训练模型。
模型评估：评估模型在测试集上的表现。
参数调优：通过调整SVM参数来优化模型性能。

加载预处理

在这里插入图片描述

def load_images(image_dir, image_size, n_samples):images = np.zeros((n_samples, image_size[0] * image_size[1]))labels = np.zeros(n_samples)for i, file in enumerate(os.listdir(image_dir)[:n_samples]):# 读取图片，转换为灰度img = imread(os.path.join(image_dir, file), as_gray=True)# 调整图片大小img_resized = resize(img, image_size, anti_aliasing=True).flatten()images[i] = img_resizedlabels[i] = get_label_from_filename(file)  # 定义一个函数来从文件名获取标签print(labels[i])return images, labelsdef get_label_from_filename(filename):# 这里应该根据实际情况来实现如何从文件名获取标签return int(filename.split('_')[0])

加载

image_dir = 'mnist_images'  # 图片文件夹路径
image_size = (28, 28)  # 图片大小
n_samples = 100  # 
X, y = load_images(image_dir, image_size, n_samples)

预处理：零均值归一化处理

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

划分测评集

# 首先，分割出训练集和一个临时测试集，这里将20%的数据作为这个临时集合
X_train, X_temp, y_train, y_temp = train_test_split(X_scaled, y, test_size=0.2, random_state=42)# 然后，将这个临时测试集进一步分割为真正的测试集和验证集，这里我们把它们各自占原始数据集的比例设置为10%
X_test, X_val, y_test, y_val = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)

我们首先保留了20%的数据作为非训练数据（X_temp, y_temp），这部分数据不会用于模型训练。然后我们把这20%的数据一分为二，一半作为测试集（X_test, y_test），一半作为验证集（X_val, y_val）。这样，训练集、测试集和验证集各自占原始数据集的80%、10%和10%。

模型训练

model = SVC(kernel='rbf', gamma=0.001, C=50)
model.fit(X_train, y_train)

kernel参数指定了SVM内核函数的类型，它用于将输入数据映射到高维空间，‘rbf’，高斯核。用于非线性可分的情况

gamma参数只对’rbf’、'poly’和’sigmoid’核函数有影响。它定义了单个训练样本达到多大程度的远距离影响。具体来说，gamma的值越大，每个样本的影响范围就越小，这会导致决策边界更加复杂，可能导致过拟合。相反，较小的gamma值意味着样本具有更大的影响范围，导致决策边界更加平滑。

C惩罚因子，较小的C值鼓励模型选择更简单的决策边界（边界更平滑），即使这会导致一些训练样本被分类错误。较大的C值会尝试正确分类所有训练样本，即使这意味着决策边界更加复杂，这可能会导致模型过拟合。

模型评估

算召回率（Recall）、精确度（Precision）等指标时，average参数的选择对最终结果有重大影响。
1. average='micro'
作用：先计算模型在所有类别上的总真正例、假正例和假反例，然后用这些总数来计算总体的指标。
应用场景：当你希望指标能反映出被分类为每个类别的样本的比例时，特别适用于样本不平衡的情况。micro方法将所有类别的贡献视为相等，主要关注的是每个样本是否被正确分类。
2. average='macro'
作用：为每个类别单独计算指标，然后计算这些指标的未加权平均值。这意味着所有类别都被视为同等重要，不考虑它们在数据集中的比例。
应用场景：当你认为每个类别都同等重要时，无论它们的样本量大小。这适用于你希望模型在所有类别上表现均衡，即使某些类别的样本数量较少。
3. average='weighted'
作用：为每个类别单独计算指标，然后计算这些指标的加权平均值，权重与每个类别的真实样本数量成比例。这意味着较多样本的类别在总体指标中占有更大的比重。
应用场景：适用于你更关心多数样本的类别，特别是在样本不平衡时。它有助于反映模型在最多数类上的性能表现。
4. average='samples'（仅适用于多标签问题）
作用：计算每个实例的指标，然后取平均。这种方法仅适用于多标签分类问题。
应用场景：当你的任务是多标签分类，即一个样本可以同时属于多个类别时。

# 预测和评估
# 打印验证集上的性能指标
print("性能评估（验证集）:")
print(classification_report(y_val, y_val_pred))# 假设基于验证集的评估结果你决定了最终的模型参数
# 现在使用测试集来评估最终模型的性能
y_test_pred = model.predict(X_test)# 打印测试集上的性能指标
print("性能评估（测试集）:")
print(classification_report(y_test, y_test_pred))

准确率（Accuracy）：准确率是最直观的性能指标，它衡量的是分类正确的样本占总样本数的比例。在处理不平衡数据集时，它可能不是一个好的选择，因为即使模型仅预测数量较多的类别，准确率也可能很高。
召回率（Recall）：召回率是在所有实际正类中，被正确预测为正类的比例。它是对模型找回所有正样本能力的衡量。召回率越高，意味着较少的实际正类被漏判为负类。公式为：正确预测为正类的样本数/正类的样本数
精确度（Precision）：精确度是在所有预测为正类的样本中，实际为正类的比例。它衡量的是模型预测正类的准确性。在需要确保预测正类的质量较高的应用中，精确度是一个关键的指标。

参数调优

实现自动化调参
对于超参数调整，scikit-learn提供了GridSearchCV和RandomizedSearchCV等工具

全面搜索：GridSearchCV通过遍历给定的参数网格中的所有参数组合来寻找最佳的超参数。这意味着如果你提供了大量的参数和/或参数值，它将尝试这些参数的每一种可能组合。
计算成本：由于需要遍历所有可能的参数组合，所以当参数空间很大时，GridSearchCV可能会非常耗时。
结果：它保证能找到参数空间中的最佳组合（假设在给定的参数网格中）。
使用场景：当参数空间相对较小，且计算资源充足时，使用GridSearchCV比较合适。
RandomizedSearchCV
随机搜索：RandomizedSearchCV通过从指定的参数分布中随机采样参数组合进行搜索。你可以设定一个预算（比如迭代次数），它将在这个预算下随机选择参数组合进行尝试。
计算成本：相比于GridSearchCV，RandomizedSearchCV通常更快，因为它不需要尝试所有可能的参数组合，而是随机选取。
结果：虽然RandomizedSearchCV不能保证找到参数空间中的最佳组合，但在实践中，它往往能够在合理的时间内找到非常好的结果，特别是在某些参数对模型性能的影响远大于其他参数的情况下。
使用场景：当参数空间很大或者计算资源有限时，RandomizedSearchCV是一个更好的选择。

如果你确切知道哪些参数范围是重要的，并且参数空间相对较小，GridSearchCV可以全面地搜索这些参数，以找到最优解。
如果参数空间很大，你想在有限的时间内找到一个“足够好”的解，或者当某些参数对模型性能的影响显著大于其他参数时，RandomizedSearchCV是一个更高效的选择。

# 设置参数网格
param_grid = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001], 'kernel': ['rbf', 'linear']}# 创建网格搜索对象
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2)
grid.fit(X_val, y_val)# 查看最佳参数
# 设置参数网格
param_grid = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001], 'kernel': ['rbf', 'linear']}
# 创建网格搜索对象，这里我们使用训练集和验证集进行网格搜索
# 注意：可以通过交叉验证在训练集上自动分割出验证集，这样不需要手动分割验证集
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2, cv=5)
grid.fit(X_train, y_train)
# 查看最佳参数
print("最佳参数：", grid.best_params_)
# 使用找到的最佳参数创建新的SVM模型
best_model = grid.best_estimator_# 首先在验证集上进行评估，验证集用于模型选择和调参，已经通过交叉验证间接使用
y_val_pred = best_model.predict(X_val)
print("性能评估（验证集）:")
print(classification_report(y_val, y_val_pred))# 现在使用测试集来评估最终模型的性能
y_test_pred = best_model.predict(X_test)
print("性能评估（测试集）:")
print(classification_report(y_test, y_test_pred))

查看结果

训练下来结果如下：

Fitting 5 folds for each of 32 candidates, totalling 160 fits
[CV] END .........................C=0.1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=0.1, gamma=1, kernel=rbf; total time=   0.0s
D:\herche_study\herche_py_study\djongo_demo\Lib\site-packages\sklearn\model_selection\_split.py:737: UserWarning: The least populated class in y has only 4 members, which is less than n_splits=5.warnings.warn(
[CV] END .........................C=0.1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=0.1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=0.1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ......................C=0.1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=0.1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=0.1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=0.1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=0.1, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=0.1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=0.1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=0.1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=0.1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=0.1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ....................C=0.1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=0.1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=0.1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=0.1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=0.1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=0.1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=0.1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=0.1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=0.1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=0.1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ...................C=0.1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=0.1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=0.1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=0.1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=0.1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=0.1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=0.1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=0.1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=0.1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=0.1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ..................C=0.1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=0.1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=0.1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=0.1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=0.1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ...........................C=1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ...........................C=1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ...........................C=1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ...........................C=1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ...........................C=1, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ........................C=1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ........................C=1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ........................C=1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ........................C=1, gamma=1, kernel=linear; total time=   0.0s
[CV] END ........................C=1, gamma=1, kernel=linear; total time=   0.0s
[CV] END .........................C=1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .........................C=1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .........................C=1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .........................C=1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .........................C=1, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ......................C=1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=1, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ........................C=1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ........................C=1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ........................C=1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ........................C=1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ........................C=1, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END .....................C=1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=1, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .......................C=1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .......................C=1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .......................C=1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .......................C=1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .......................C=1, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ....................C=1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ....................C=1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ....................C=1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ....................C=1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ....................C=1, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..........................C=10, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ..........................C=10, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ..........................C=10, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ..........................C=10, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ..........................C=10, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .......................C=10, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=10, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=10, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=10, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=10, gamma=1, kernel=linear; total time=   0.0s
[CV] END ........................C=10, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ........................C=10, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ........................C=10, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ........................C=10, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ........................C=10, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .....................C=10, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END .....................C=10, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END .....................C=10, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END .....................C=10, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END .....................C=10, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END .......................C=10, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END .......................C=10, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END .......................C=10, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END .......................C=10, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END .......................C=10, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ....................C=10, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ....................C=10, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ....................C=10, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ....................C=10, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ....................C=10, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ......................C=10, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ......................C=10, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ......................C=10, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ......................C=10, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ......................C=10, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ...................C=10, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ...................C=10, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ...................C=10, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ...................C=10, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ...................C=10, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END .........................C=100, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=100, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=100, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=100, gamma=1, kernel=rbf; total time=   0.0s
[CV] END .........................C=100, gamma=1, kernel=rbf; total time=   0.0s
[CV] END ......................C=100, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=100, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=100, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=100, gamma=1, kernel=linear; total time=   0.0s
[CV] END ......................C=100, gamma=1, kernel=linear; total time=   0.0s
[CV] END .......................C=100, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=100, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=100, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=100, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END .......................C=100, gamma=0.1, kernel=rbf; total time=   0.0s
[CV] END ....................C=100, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=100, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=100, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=100, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ....................C=100, gamma=0.1, kernel=linear; total time=   0.0s
[CV] END ......................C=100, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=100, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=100, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=100, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ......................C=100, gamma=0.01, kernel=rbf; total time=   0.0s
[CV] END ...................C=100, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=100, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=100, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=100, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END ...................C=100, gamma=0.01, kernel=linear; total time=   0.0s
[CV] END .....................C=100, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=100, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=100, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=100, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END .....................C=100, gamma=0.001, kernel=rbf; total time=   0.0s
[CV] END ..................C=100, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=100, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=100, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=100, gamma=0.001, kernel=linear; total time=   0.0s
[CV] END ..................C=100, gamma=0.001, kernel=linear; total time=   0.0s
最佳参数： {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
性能评估（验证集）:precision    recall  f1-score   support0.0       0.75      1.00      0.86         32.0       0.00      0.00      0.00         13.0       1.00      1.00      1.00         14.0       1.00      1.00      1.00         27.0       1.00      1.00      1.00         28.0       1.00      1.00      1.00         1accuracy                           0.90        10macro avg       0.79      0.83      0.81        10
weighted avg       0.82      0.90      0.86        10性能评估（测试集）:
D:\herche_study\herche_py_study\djongo_demo\Lib\site-packages\sklearn\metrics\_classification.py:1471: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior._warn_prf(average, modifier, msg_start, len(result))
D:\herche_study\herche_py_study\djongo_demo\Lib\site-packages\sklearn\metrics\_classification.py:1471: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior._warn_prf(average, modifier, msg_start, len(result))
D:\herche_study\herche_py_study\djongo_demo\Lib\site-packages\sklearn\metrics\_classification.py:1471: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior._warn_prf(average, modifier, msg_start, len(result))precision    recall  f1-score   support0.0       1.00      1.00      1.00         11.0       1.00      1.00      1.00         22.0       1.00      1.00      1.00         13.0       1.00      1.00      1.00         14.0       1.00      1.00      1.00         16.0       1.00      1.00      1.00         17.0       1.00      1.00      1.00         29.0       1.00      1.00      1.00         1accuracy                           1.00        10macro avg       1.00      1.00      1.00        10
weighted avg       1.00      1.00      1.00        10

验证模型

保存模型

model_filename = 'best_model.joblib'
dump(best_model, model_filename)

验证模型，我们下载了100个测试数据在这里插入图片描述

用于验证这个模型的性能：

X,y = load_images('test_images',(28, 28),100)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
loaded_model = load('best_model.joblib')
# 使用加载的模型进行预测
y_pred = loaded_model.predict(X_scaled)
# 计算准确率
print("性能评估（验证集）:")
print(classification_report(y, y_pred))

结果是：

性能评估（验证集）:precision    recall  f1-score   support0.0       0.80      1.00      0.89         81.0       0.85      0.92      0.88        122.0       0.88      0.50      0.64        143.0       0.83      1.00      0.91        104.0       0.82      0.90      0.86        105.0       0.80      0.50      0.62         86.0       0.78      0.88      0.82         87.0       1.00      0.91      0.95        118.0       1.00      0.71      0.83         79.0       0.71      1.00      0.83        12accuracy                           0.83       100macro avg       0.85      0.83      0.82       100
weighted avg       0.84      0.83      0.82       100

这个性能评估报告提供了模型在验证集上对于一个十类分类问题的详细性能分析。这里的验证集共有100个样本。

各类的表现
类别0至类别9：报告显示了每个类别的精确度（Precision）、召回率（Recall）和F1分数（F1 Score）。精确度衡量的是模型预测为该类别的样本中，实际属于该类别的比例；召回率衡量的是实际属于该类别的样本中，被模型正确预测的比例；F1分数是精确度和召回率的调和平均，用于评价模型的综合性能。类别2和类别5：这两个类别的召回率相对较低（分别为0.50），意味着模型错过了一半实际属于这些类别的样本。类别2的精确度相对较高（0.88），而类别5的精确度（0.80）说明在预测为这个类别的样本中，有20%实际不属于此类。类别8和类别9：尽管这两个类别的精确度非常高（分别为1.00和0.71），但它们的召回率不是很平衡，特别是类别8的召回率只有0.71，意味着有约29%的实际属于类别8的样本被模型错过了。总结
这个模型在多数类别上表现良好，特别是一些类别达到了很高的精确度和召回率。但是，对于某些类别（如类别2和类别5），模型在召回率上的表现不足，这可能指出模型对这些类别的识别存在困难。这可能是由于样本不足、特征不明显或类间差异不大等原因造成的。

结束

(当使用SVC()类创建SVM模型并调用.fit(X_train, y_train)方法进行训练时，SVM算法会自动寻找最大化边界间隔的超平面。这个过程包括确定哪些训练样本作为支持向量，以及如何通过这些支持向量来定义最优的决策边界。这一部分是SVM算法的内部机制，不需要开发者手动实现。间隔是决策边界与最近的训练样本之间的距离，这些最近的样本就是支持向量。SVM模型通过最大化这个间隔来提高模型的泛化能力。在SVC()类中，参数C起到控制误差的权重，间接影响间隔大小的作用。较小的C值允许较大的间隔，提高模型的泛化能力，而较大的C值会尽量减少误分类，但可能导致间隔变小，增加过拟合的风险。)

优点
效果好：在许多实际应用中，特别是在维度较高的数据集上，SVM常常表现出优秀的性能。
泛化能力强：通过最大化间隔，SVM能够提高模型的泛化能力，降低过拟合的风险。
灵活性：通过选择合适的核函数，SVM可以很好地处理线性和非线性数据。

缺点
计算开销：对于大规模数据集，SVM的训练时间可能会比较长。
参数选择：SVM的性能高度依赖于核函数参数（如RBF核的γ）和正则化参数C的选择。不恰当的参数设置可能导致模型过拟合或欠拟合。
结果解释性：与一些简单模型（如决策树）相比，SVM模型的结果解释性较差。

应用
分类任务：SVM最常用于分类问题，尤其是二分类问题。
回归任务：通过引入ε-不敏感损失函数，SVM也可以用于回归任务（称为SVR）。
异常检测：SVM的一个变种可以用于异常检测任务。

支持向量机是一种强大的学习算法，适用于各种机器学习任务。通过合理选择核函数和调整参数，SVM可以在多种数据集上实现高精度的模型性能。