【问题描述】
小蓝要上一个楼梯,楼梯共有 n 级台阶(即小蓝总共要走 n 级)。小蓝每一步可以走 a 级、b 级或 c 级台阶。
请问小蓝总共有多少种方案能正好走到楼梯顶端?
【输入格式】
输入的第一行包含一个整数 n 。
第二行包含三个整数 a, b, c 。
【输出格式】
输出一行包含一个整数,表示答案。答案可能很大,请输出答案除以 1000000007 后的余数。
【样例输入】
4
1 2 3
【样例输出】
7
【评测用例规模与约定】
对于 30% 评测用例,1 <= a < b < c <= n <= 50。
对于 60% 评测用例,1 <= a < b < c <= n <= 1000。
对于所有评测用例,1 <= a < b < c <= n <= 1000000。
【算法分析】
● 本例用到的 vector 语法简介
vector<int> v(10); // 定义了10个 int 类型元素的向量 v,未初始化;
vector<int> v(10,1); //定义了10个 int 类型元素的向量 v,每个元素初始化为1。
● 1000000007,是最小的十位数质数。模1000000007,可以保证值永远在 int 的范围内。
● 此题解法,可由题目 https://blog.csdn.net/hnjzsyjyj/article/details/114990369 使用的“最后一步法”获得启发。由于本题是它的加难版本,本质上一致,所以本题亦可利用动态规划问题的“最后一步法”尝试求解。
据上,设状态 f(x) 表示走到第 x 阶台阶时共有多少种走法。进而,可确立状态转移方程为 f(n)=f(n-a)+f(n-b)+f(n-c)。但是,a、b、c 是在程序运行后输入的,是不定的。所以,无法预先根据 a、b、c 的值,依据“最后一步法”在代码中确定相应的边界条件。故在代码上,就需要有所变化,即不以a、b、c 的值作为确立边界的条件,而是以 a、b、c 的值作为分段计算的条件,进行累加计算。如下图所示。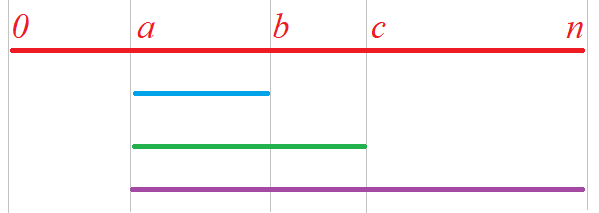
也就是说,最终合并计算的值就是状态转移方程 f(n)=f(n-a)+f(n-b)+f(n-c) 要确立的值。
【算法代码】
#include <bits/stdc++.h>
using namespace std;int main() {int n,a,b,c;cin>>n>>a>>b>>c;vector<int> v(n+1,0);v[0]=1;for(int i=a; i<=n; i++) {v[i]=(v[i]+v[i-a])%1000000007;if(i>=b) v[i]=(v[i]+v[i-b])%1000000007;if(i>=c) v[i]=(v[i]+v[i-c])%1000000007;}cout<<v[n]<<endl;return 0;
}/*
in:
4
1 2 3out:
7
*/若依据本题解法思路,则题目 https://blog.csdn.net/hnjzsyjyj/article/details/114990369 的代码如下所示:
#include <bits/stdc++.h>
using namespace std;int a=1,b=2,c=3;int main() { int n;cin>>n;vector<int> v(n+1,0);v[0]=1;for(int i=a; i<=n; i++) {v[i]=(v[i]+v[i-a])%1000000007;if(i>=b) v[i]=(v[i]+v[i-b])%1000000007;if(i>=c) v[i]=(v[i]+v[i-c])%1000000007;}cout<<v[n]<<endl;return 0;
}/*
in:5
out:13
*/
【参考文献】
https://www.ewbang.com/community/article/details/997972208.html
https://blog.csdn.net/weixin_45697711/article/details/121579057
https://blog.csdn.net/weixin_73332175/article/details/136502012
)







汇编mov、addsub指令)









)
