后端之卡尔曼滤波
前言
在很久之前,人们刚结束信息传递只能靠信件的时代,通信技术蓬勃发展,无线通信和有线通信走进家家户户,而著名的贝尔实验室就在这个过程做了很多影响深远的研究。为了满足不同电路和系统对信号的需求,比如去除噪声,或者区分不同频率的信号,滤波器就诞生了,而贝尔实验室就是这一领域研究的先行者。早期的滤波器是电子滤波器,是由电阻,电感,电容等电子元件组成的物理电路,其电路图大概长这样:
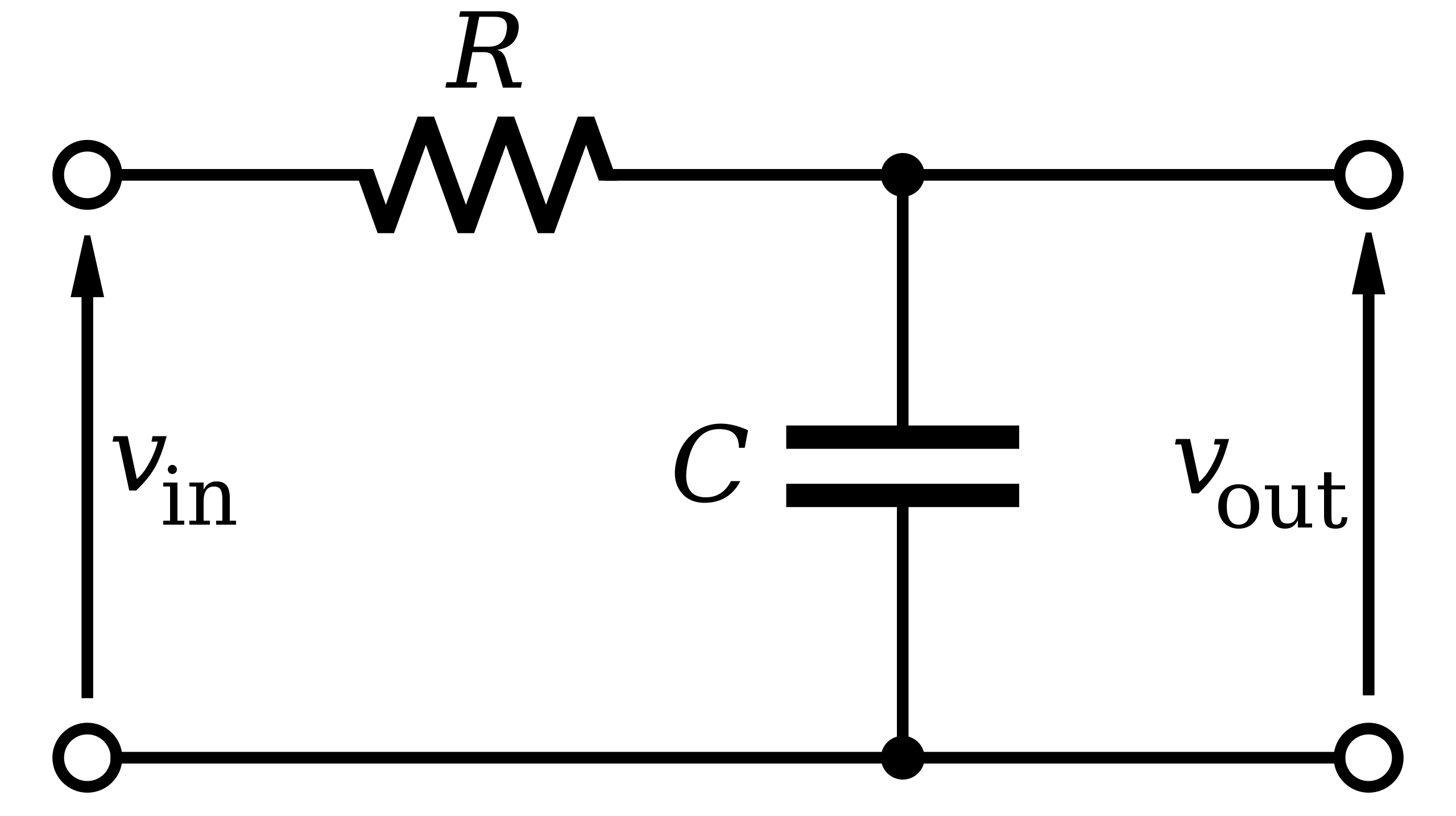
这个是由一个电容和一个电阻组成的RC滤波器。而装在实际家电或者设备中的滤波器大概如下图,这个是一个包含高通和低通滤波器的信号分离装置。
随着技术的发展(主要是计算机的兴起),相比于处理原始模拟信号,人们更愿意处理数字信号,这可以带来更高的处理速度,更低的成本和更高的精度,于是,数字滤波器诞生了。数字滤波器是对数字信号进行滤波处理以得到期望的响应特性的离散时间系统。这时候数字模拟器还是依靠基本的一些电路元件比如寄存器,延时器,加法器等,但其工作的领域已变为经过数模转换器转化后的数字信号域了,后面广泛用于收音机,蜂窝电话等设备中。
数字滤波器早期主要处理信号,而信号都是一些波形,这也是滤波的由来。后面随着人们对滤波器的扩展,出现了另外一种形式的数字滤波器,其工作过程包含状态空间模型,称为状态空间滤波器,状态空间滤波器的一个典型例子是Rudolf Kalman在1960年提出的卡尔曼滤波器。这时候虽然没有了波,主要是空间状态,但按传统,这个名称还是保留了下来。
最后,随着计算机的发展,中央处理器(CPU)集成了各种计算单元,所有计算任务都可以交给它,数字滤波器就不用单独保留如寄存器,加法器等元件了,在保留了算法原理和流程之后羽化成仙,成为了滤波算法。
卡尔曼滤波算法推导简明版
发明了卡尔曼滤波算法的人,叫做鲁道夫·埃米尔·卡尔曼,是一个匈牙利人。
卡尔曼滤波是基于马尔科夫假设的,即下一时刻状态只与上一时刻有关。其主要针对于线性高斯系统,计算的流程如下:
假设状态 X \mathbf{X} X的转移方程为:

其中 F k \mathbf{F}_{k} Fk为状态转移矩阵,而 P k \mathbf{P}_{k} Pk为 X k \mathbf{X}_{k} Xk的方差
X \mathbf{X} X只表示自身的状态,另外一些系统还会有外部控制因数,比如火车减速时,速度是状态量,但可以有刹车装置进行减速,如果系统存在这部分控制因数,需要把这部分加到状态转移中:
x ^ k = F k x ^ k − 1 + B u k P k = F k P k − 1 F k T \begin{aligned} \hat{\mathbf{x}}_{k} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k\\ \mathbf{P}_{k} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} \end{aligned} x^kPk=Fkx^k−1+Buk=FkPk−1FkT
另外, X \mathbf{X} X中包含环境的一些未知变量,我们假设为噪声,同时噪声分布假设服从高斯分布,于是有如下方程:
x ^ k = F k x ^ k − 1 + B u k + w k P k = F k P k − 1 F k T + R \begin{aligned} \hat{\mathbf{x}}_{k} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k +w_k\\ \mathbf{P}_{k} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} +R \end{aligned} x^kPk=Fkx^k−1+Buk+wk=FkPk−1FkT+R
卡尔曼滤波中,还需要使用观测方程来更新,一般观测方程是需要从状态变为观测量的,即需要有一个观测量到状态的转换,但很多时候这个转换方程都没有,但这并不影响我们假设,如果没有转换方程,到时候直接把转换矩阵设为单位矩阵就行,那现在假设观测方程为:
z k = H ∗ x k + v k z_k = H*x_k+v_k zk=H∗xk+vk
其中 H H H为观测方程, v k v_k vk为观测的噪声分布,假设其服从 v k ∼ N ( 0 , Q ) v_k\sim N\left(0,Q\right) vk∼N(0,Q),即零均值,方差为Q的高斯分布:
到这里,需要说明一点,上一次滤波的结果,会作为下一次滤波的初始值,即由上一次后验概率,通过状态转移矩阵与控制向量,变为目前的先验值,所以原来的观测方程需要变为:
x ^ k ˉ = F k x ^ k − 1 + B u k + w k P k ˉ = F k P k − 1 F k T + R \begin{aligned} \hat{\mathbf{x}}_{\bar{k}} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k +w_k\\ \mathbf{P}_{\bar{k}} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} +R \end{aligned} x^kˉPkˉ=Fkx^k−1+Buk+wk=FkPk−1FkT+R
其中下标不带横杠的,表示后验值,带横杠的,代表先验值,这样就由上一时刻的最优估计,得到了当前预测的先验状态及先验方差。
对于观测方程,其方差主要由观测方差决定,即:
P z k = R P_{z_k} = R Pzk=R
zk的均值为Hxk,即zk服从N(Hxk,R)的分布。
这两个分布都是高斯分布,一个是状态的先验分布,一个是传感器测量的分布,这个测量与xk的状态也有关,现在要求这两个分布的联合分布,并求其最大值,很简单,把两个分布乘起来,由于高斯分布的乘积,还是高斯分布,取其均值处,就是概率最大的状态。

乘积的部分,就是所说的状态更新,首先由高斯分布的公式可得:
N ( x , μ , σ ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 \mathcal{N}(x, \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} N(x,μ,σ)=σ2π1e−2σ2(x−μ)2
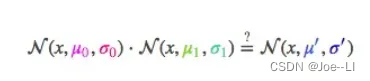
那么两个分布相乘,系数结果为:
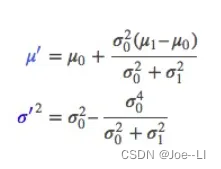
其中均值u就是概率最大时的值,σ就是方差,其中这个式子就是最后我们要求的,但这个式子有点复杂,于是用一个系数化简为:
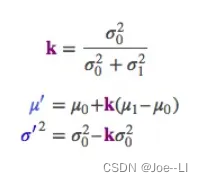
其中k称为卡尔曼增益,u0为预测值,u1为观测。可以看到,k为0到1之间的数,分子为预测的方差,如果预测方差越大,则越向观测值靠拢,如果预测方差越小,则越向预测值靠拢。
截至目前,我们有用矩阵 ( μ 0 , Σ 0 ) = ( H k x ^ k , H k P k H k T ) \left(\mu_0, \Sigma_0\right)=\left(H_k \hat{x}_k, H_k P_k H_k^T\right) (μ0,Σ0)=(Hkx^k,HkPkHkT)预测的分布,有用传感器读数 ( μ 1 , Σ 1 ) = ( z ⃗ k , R k ) \left(\mu_1, \Sigma_1\right)=\left(\vec{z}_k, R_k\right) (μ1,Σ1)=(zk,Rk)预测的分布。把它们代入上节的矩阵等式中:
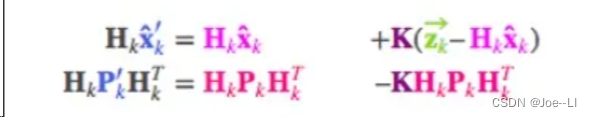
相应的,卡尔曼增益就是:
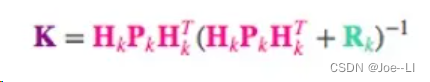
两个式子左边都有不少Hk矩阵,同时把这个矩阵去掉,则K变为:
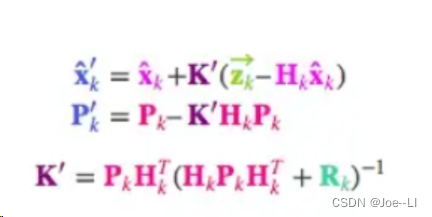
于是,我们得到最后卡尔曼更新的公式:
K k = P k − H T H P k − H T + R x ^ k = x ^ k ˉ + K k ( z k − H x ^ k ˉ ) P k = ( I − K k H ) P k ˉ \begin{array}{c} K_{k}=\frac{P_{k}^{-} H^{T}}{H P_{k}^{-} H^{T}+R} \\ \hat{x}_{k}=\hat{x}_{\bar{k}}+K_{k}\left(z_{k}-H \hat{x}_{\bar{k}}\right) \\ P_{k}=\left(I-K_{k} H\right) P_{\bar{k}} \end{array} Kk=HPk−HT+RPk−HTx^k=x^kˉ+Kk(zk−Hx^kˉ)Pk=(I−KkH)Pkˉ
其中计算K的都是使用先验方差,R为传感器方差。
Zk为实际观测值,Hxk为预测的观测值。
最后使用K及先验方差,得到后验方差及后验均值。
参考链接:
https://zhuanlan.zhihu.com/p/39912633
https://www.guyuehome.com/










)

)


)



