[1]Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).
[2] [论文简析]VAE: Auto-encoding Variational Bayes[1312.6114]
[3] The Reparameterization Trick
[4] 变分法的基本原理是什么?
文章目录
- 1-什么是VAE
- 1.1-目标
- 1.2-Intractability:
- 1.3-Approximation use NN:
- 1.4-最大化 L ( θ , ϕ ; x ) L(\theta,\phi;x) L(θ,ϕ;x):
- 1.5-优化 E q ϕ ( z ∣ x ) [ log ( p θ ( x ∣ z ) ) ] E_{q_\phi(z|x)}[\log(p_\theta(x|z))] Eqϕ(z∣x)[log(pθ(x∣z))]和 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ) ) D_{KL}(q_\phi(z|x)||p_\theta(z)) DKL(qϕ(z∣x)∣∣pθ(z)):
- 1.6-重参数化技巧
- 1.7-SGVB
- 1.8-另外一种SGVB
- 1.9.总结
- 1.10-变分的含义
1-什么是VAE
1.1-目标
x \mathbf{x} x:为 z \mathbf{z} z的采样,生成自条件分布 p θ ∗ ( x ∣ z ) p_{\theta^*}(\mathbf{x}|\mathbf{z}) pθ∗(x∣z)( θ ∗ \theta^* θ∗表示ground truth而 θ \theta θ表示解码器参数),;
z \mathbf{z} z: x \mathbf{x} x更本质的描述(不可直接观测),来自先验分布 p θ ∗ ( z ) p_{\boldsymbol{\theta}^*}(\mathbf{z}) pθ∗(z);
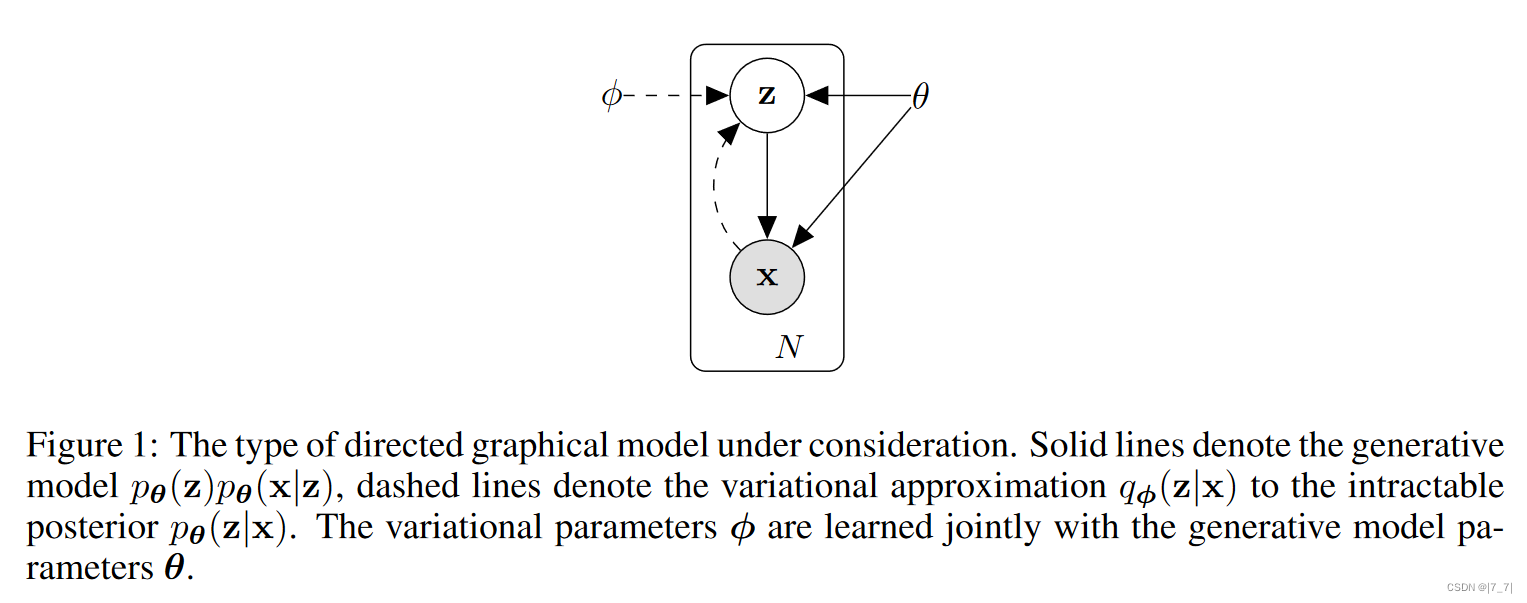
目标是是根据 x \mathbf{x} x能够得到 z \mathbf{z} z:
1.2-Intractability:
- p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z \begin{array}{rcl}p_{\boldsymbol{\theta}}(\mathbf{x})&=&\int p_{\boldsymbol{\theta}}(\mathbf{z})p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})d\mathbf{z}\end{array} pθ(x)=∫pθ(z)pθ(x∣z)dz,因为在实际情况下,潜在变量 z \mathbf{z} z的维度可能很高,或者先验分布 p θ ∗ ( z ) p_{\boldsymbol{\theta}^*}(\mathbf{z}) pθ∗(z)和条件分布 p θ ∗ ( x ∣ z ) p_{\theta^*}(\mathbf{x}|\mathbf{z}) pθ∗(x∣z)可能是复杂的非线性函数。因此,直接计算这个积分是不可行的。
VAE采用了一种变分推断的方法来近似计算这个积分。具体来说,VAE使用了变分下界(ELBO),通过优化ELBO来近似计算这个积分。这种方法将原本的推断问题转化为一个优化问题,并且通过优化方法(如随机梯度下降)来求解。尽管使用ELBO进行近似推断使得VAE的训练变得可行,但这仍然是一个近似方法,其精度取决于所选的变分分布族和优化算法的选择。
- p θ ( z ∣ x ) = p θ ( x ∣ z ) p θ ( z ) / p θ ( x ) p_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x})=p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol{\theta}}(\mathbf{z})/p_{\boldsymbol{\theta}}(\mathbf{x}) pθ(z∣x)=pθ(x∣z)pθ(z)/pθ(x)中的 p θ ( x ) p_{\boldsymbol{\theta}}(\mathbf{x}) pθ(x)未知 (贝叶斯公式,在观察到数据后,对事件发生概率进行推断的过程,通过计算后验概率,根据观察到的数据进行推断,并更新对事件发生概率的认识)。
1.3-Approximation use NN:
p θ ( z ∣ x ) ≅ q ϕ ( z ∣ x ) p_\theta(\mathbf{z}|\mathbf{x})\cong q_\phi(\mathbf{z}|\mathbf{x}) pθ(z∣x)≅qϕ(z∣x),用KL散度评估两个分布的相似程度:
D K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) = − ∑ z q ϕ ( z ∣ x ) log ( p θ ( z ∣ x ) q ϕ ( z ∣ x ) ) = − ∑ z q ϕ ( z ∣ x ) log ( p θ ( x , z ) p θ ( x ) q ϕ ( z ∣ x ) ) = − ∑ z q ϕ ( z ∣ x ) [ log ( p θ ( x , z ) q ϕ ( z ∣ x ) ) − log ( p θ ( x ) ) ] \begin{aligned} D_{KL}(q_{\phi}(\mathbf{z|x})||p_{\theta}(\mathbf{z|x}))&=-\sum_{\mathbf{z}}q_{\phi}(\mathbf{z|x})\log\left(\frac{p_{\theta}(\mathbf{z|x})}{q_{\phi}(\mathbf{z|x})}\right)\\ &=-\sum_{\mathbf{z}}q_{\phi}(\mathbf{z|x})\log\left(\frac{\frac{p_{\theta}(\mathbf{x,z})}{p_{\theta}(\mathbf{x})}}{q_{\phi}(\mathbf{z|x})}\right) \\ &=-\sum_zq_\phi(\mathbf{z|x})\left[\log\left(\frac{p_\theta(\mathbf{x,z})}{q_\phi(\mathbf{z|x})}\right)-\log(p_\theta(\mathbf{x}))\right] \end{aligned} DKL(qϕ(z∣x)∣∣pθ(z∣x))=−z∑qϕ(z∣x)log(qϕ(z∣x)pθ(z∣x))=−z∑qϕ(z∣x)log qϕ(z∣x)pθ(x)pθ(x,z) =−z∑qϕ(z∣x)[log(qϕ(z∣x)pθ(x,z))−log(pθ(x))]
log ( p θ ( x ) ) \log(p_\theta(\mathbf{x})) log(pθ(x))与 z \mathbf{z} z无关是常数,所以和 q ϕ ( z ∣ x ) q_\phi(\mathbf{z|x}) qϕ(z∣x)相乘可以提到求和符号外面,而 q ϕ ( z ∣ x ) q_\phi(\mathbf{z|x}) qϕ(z∣x)对 z \mathbf{z} z求和结果为1,等号左右换项:
log ( p θ ( x ) ) = K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) + ∑ z q ϕ ( z ∣ x ) log ( p θ ( x , z ) q ϕ ( z ∣ x ) ) = D K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) + L ( θ , ϕ ; x ) \begin{aligned}\begin{aligned}\log(p_\theta(x))&=KL(q_\phi(z|x)||p_\theta(z|x))+\sum_zq_\phi(z|x)\log\left(\frac{p_\theta(x,z)}{q_\phi(z|x)}\right)\\&=D_{KL}(q_\phi(z|x)||p_\theta(z|x))+L(\theta,\phi;x)\end{aligned}\end{aligned} log(pθ(x))=KL(qϕ(z∣x)∣∣pθ(z∣x))+z∑qϕ(z∣x)log(qϕ(z∣x)pθ(x,z))=DKL(qϕ(z∣x)∣∣pθ(z∣x))+L(θ,ϕ;x)
左边是常数,KL散度非负,所以最大化 L ( θ , ϕ ; x ) L(\theta,\phi;x) L(θ,ϕ;x)(称之为Variational lower bound)就可以实现 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) D_{KL}(q_\phi(z|x)||p_\theta(z|x)) DKL(qϕ(z∣x)∣∣pθ(z∣x))最小化;\
1.4-最大化 L ( θ , ϕ ; x ) L(\theta,\phi;x) L(θ,ϕ;x):
L ( θ , ϕ ; x ) = ∑ z q ϕ ( z ∣ x ) log ( p θ ( x , z ) q ϕ ( z ∣ x ) ) = ∑ z q ϕ ( z ∣ x ) log ( p θ ( x ∣ z ) p θ ( z ) q ϕ ( z ∣ x ) ) = ∑ z q ϕ ( z ∣ x ) [ log ( p θ ( x ∣ z ) ) + log ( p θ ( z ) q ϕ ( z ∣ x ) ) ] = E q ϕ ( z ∣ x ) [ log ( p θ ( x ∣








)

)
(内含立例题))
![每日一题 --- 有效的字母异位词[力扣][Go]](http://pic.xiahunao.cn/每日一题 --- 有效的字母异位词[力扣][Go])



![[AutoSar]BSW_ECUC模块介绍](http://pic.xiahunao.cn/[AutoSar]BSW_ECUC模块介绍)
卷积 | 改进Ghost卷积轻量化网络)

)