摘要
知识图嵌入方法学习知识图中实体和关系的低维向量表示,便于知识图中的链接预测任务。在学习嵌入过程中,采样负三元组是很重要的,因为KGs只观察到正三元组。据我们所知,均匀随机、基于生成对抗网络(GAN)和nscach、结构感知负抽样(SANS)是文献中提到的四种负抽样方法。不幸的是,它们存在计算和内存效率低下的问题。此外,由于采样的负三元组质量差,它们的预测性能受到“梯度消失”问题的影响。在本文中,我们提出了一种简单的负采样(SNS)方法,该方法基于在嵌入空间中离损坏实体更近的实体能够提供高质量的负三重组的假设。此外,SNS具有良好的开发潜力,因为它使用采样的高质量底片来提高负三元组的质量。在WN18、WN18RR、FB15K、FB15K-237、YAGO3-10这5个已知的知识图数据集上,通过链路预测任务对我们的采样方法进行了评价。该方法还在一个新的生物KG数据集(FIGHT-HF-23R)上进行了评估。实验结果表明,SNS提高了KG嵌入模型的预测性能,优于现有的采样方法。
3 The proposed SNS method
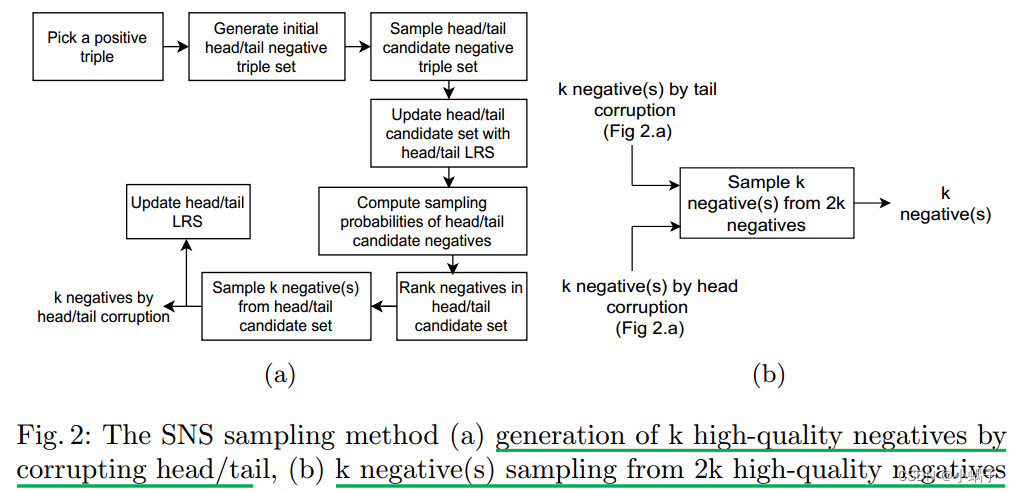
在下文中,我们描述了我们提出的用于负样本生成的SNS方法。SNS方法旨在生成高质量的负三元组,以避免均匀随机抽样的“梯度消失”问题、基于gan的抽样的复杂参数优化问题和nscach的内存需求过大问题。图2a给出了SNS采样的基本步骤。步骤如下所示:
Step 1. Triple perturbation:
从图2a开始,SNS首先通过positive triple perturbation生成正三重的初始负集。这一步与其他抽样方法类似。在triple perturbation中,正三重的头/尾通过用实体集(E)中的其他实体替换头/尾而被破坏。同时,检查负集合是否包含任何正三元组。为了说明这一点,考虑正三重![]() ,破坏尾部(t)得到初始负集
,破坏尾部(t)得到初始负集![]() ;
;
Step 2. Candidate set generation
一般情况下,由于KG包含大量实体,所以集合![]() 的大小较大。Zhang等人[4]描述了只有一些初始底片的质量是好的。由于每个正三元组需要很少的负值,我们从
的大小较大。Zhang等人[4]描述了只有一些初始底片的质量是好的。由于每个正三元组需要很少的负值,我们从![]() 中随机抽取N1个三元组来生成候选负集
中随机抽取N1个三元组来生成候选负集![]() 。随着训练的进行,我们希望下一个步骤的负向量的质量会更好或接近当前步骤的负向量的质量。为此,在当前步骤中采样的负极性存储在称为最近最少选择(LRS)的小结构中。
。随着训练的进行,我们希望下一个步骤的负向量的质量会更好或接近当前步骤的负向量的质量。为此,在当前步骤中采样的负极性存储在称为最近最少选择(LRS)的小结构中。![]() 保存了采样负,其中q0t和q0h分别是上一步中通过正反破坏采样的负。保存的底片将在下一步用于采样高质量的底片。将候选负集q0 1 (t)更新为包含LRS负集的
保存了采样负,其中q0t和q0h分别是上一步中通过正反破坏采样的负。保存的底片将在下一步用于采样高质量的底片。将候选负集q0 1 (t)更新为包含LRS负集的![]() 。LRS的使用旨在支持所提出的SNS方法的开发行为。它确保当前步骤的负极质量优于或至少接近前一步的负极质量。
。LRS的使用旨在支持所提出的SNS方法的开发行为。它确保当前步骤的负极质量优于或至少接近前一步的负极质量。
Step 3. Sampling probability computation:
在这一步中,我们计算候选负集q0 1 (t)中每个负的抽样概率。具有较高概率的底片被认为是高质量底片。概率是根据每个负号的距离得分来定义的。负三组的距离得分(h;r;t0 i) 2q0 1 (t)计算为损坏(t)和新实体(t ')之间的距离,如公式3所示

softmax函数对距离分数较低的候选负三元组计算较高的抽样概率。
Step 4. Negative triple sampling and LRS updating:
从候选负集,q0 1 (t)的三组按其概率降序排列,并抽样k负(s)。一个自然的选择可能是抽样top-k(成对训练时k=1,最大似然训练时k > 1)负(s)。然而,抽样前k位的负数可能会产生两个问题。首先,由于当前候选负集还包括最近最少采样(LRS)的高质量负集,因此有可能对相同的负(s)进行高重复采样(即使在许多连续的步骤中)。这种情况影响了SNS采样的探索。其次,假负三元组(看起来像高质量)的存在是不可忽视的[5]。为了解决这些问题,SNS从q 0 t中N2个排名靠前的组中随机抽取k个负组,q 0 t = f(h;r;对于用户自定义参数N2,其中N2 > k, jrank(h;r;t0)≤N2 g。
SNS重复上述过程(从初始负集生成到k个负集采样),对于头(h)损坏,采样k个负集作为q 0 h,对于正三重组q。LRS[q 0 t;Q0h]用采样的2k高质量负(s)更新。最后,我们从q 0 h [q 0 t]的2k个阴性中随机抽取k个高质量阴性(s)作为q 0 h;r;t。然后用采样的k负(s) q 0和对应的正q来训练KG嵌入模型。

)


)
)

拟合平面(二百三十四))

)


】揭秘Node.js:掌握这些常用命令,让你在开发路上风生水起!)






