一、堆排序
堆排序(升序):堆排序的思想就是先用数组模拟建大堆,然后把根结点与最后一个结点值交换,最后一个结点的值就是最大值,然后再把前(n-1)个元素重新建大堆,然后根结点与最后一个结点值交换,就找出了第二大的结点,....,重复操作就可以把数组排成有序。
总结:堆排序就是模拟建堆,然后找出最大的元素放最后一位,再找出次大的元素放倒数第二位,依次类推,最后变成有序。
为什么要建大堆?
如果建小堆的话只能找出最小的元素,后面的元素无法排序;
而建大堆可以找出最大的元素,再用最大的元素和最后一个元素换位,让最大的元素跑到最后面,再调用adjustdown(),调整建堆个数,让前n-1个数建堆,重复操作完成排序
1、 向下调整建堆
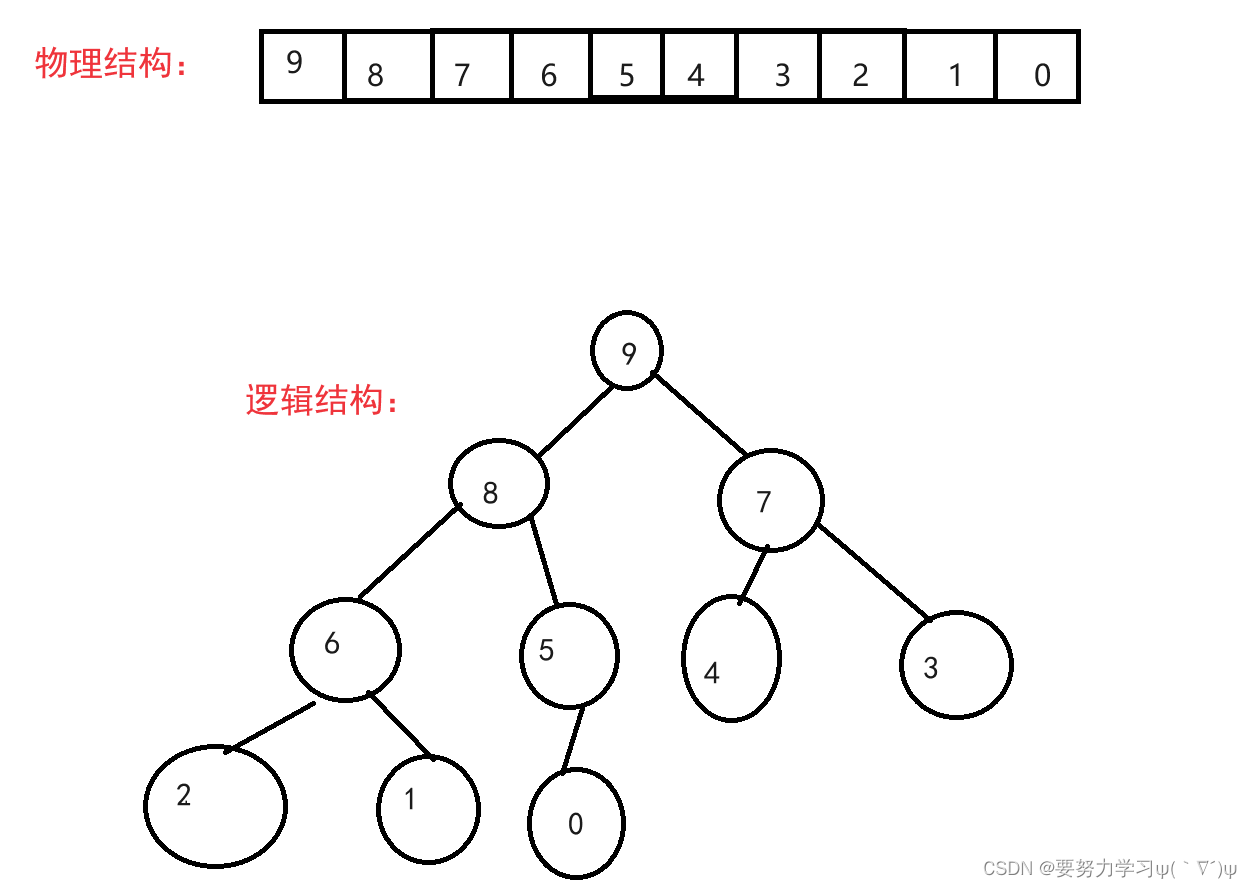
a、我们用数组看成是完全二叉树,物理结构是数组,逻辑结构是完全二叉树,大堆就是看成的完全二叉树的所有父亲结点大于自己的两个孩子 。
b、在左右子树都是大堆的情况下,根节点进行一次向下调整就可以建成大堆。
c、所以从数组最后一个元素的父亲结点开始,依次向上遍历,进行向下调整就可以满足b,
从而建成大堆。
d、(建大堆) 向下调整就是从parent结点开始与自己左右孩子中较大的那个比较大小,若parent更小,则交换值,然后parent = MinSon 继续向下比较,直到结束。
补充:在二叉树中的规律:parent =(child - 1)/ 2;
leftchild = parent * 2 + 1; rightchild = parent * 2 + 2 = leftchild + 1;
向下调整代码:
void AdjustDown(HPDataType* a, int n, int parent)//大堆
{int MinSon = parent * 2 + 1;//假定左孩子为大while (MinSon < n){if (MinSon < n - 1 && a[MinSon] < a[MinSon + 1]){MinSon++;//若左孩子更小,则将MinSon变成右孩子}if (a[MinSon] > a[parent])//如果p结点比MS结点更小,则交换{swap(&a[MinSon], &a[parent]);parent = MinSon;MinSon = parent * 2 + 1;}else{break;}}2、进行堆排序
将建好的大堆进行如下操作:
1、将首元素与尾元素互换,最大的值就已经到了末尾
2、将前n-1个值从根结点重新向下调整,因为此时左右树都是大堆,所有调整一次就能变成大堆,再重复第一步即可
堆排序代码(升序):
//升序建大堆,降序建小堆
void HeapSort(int* a, int n)
{int s = n;for (int i = (n - 2) / 2; i >= 0; i--)//向下调整建堆{AdjustDown(a, n, i);}while (n > 0)//倒着使数组有序{swap(&a[0], &a[n - 1]);n--;AdjustDown(a, n, 0);}for (int i = 0; i < s; ++i)//从0位置开始打印数组验证结果{printf("%d ", a[i]);}printf("\n");
}降序建小堆就可以了,与上面类似( •̀ ω •́ )✧
二、TopK问题
TopK问题:从 n 个数中,找出最大的前K个(n 远远大于 K)
思路:建一个K个数的小堆,让比根结点大的数进来,然后进行向下调整,重复次操作到数据结束,根节点就是K个数中最小的一个,最大的前K个数也找出来了。
TopK问题代码:
//TopK
void PrintTopK(int k)
{FILE* f = fopen("data.txt", "r");if (f == NULL){perror("fopen fail");exit(-1);}int* a = (int*)malloc(sizeof(int) * k);//a就是要建的堆if (a == NULL){perror("malloc fail");exit(-1);}for (int i = 0; i < k; ++i)//从文件读取K个数据{fscanf(f, "%d", &a[i]);}//然后建堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(a, k, i);}int x = 0;while (fscanf(f, "%d", &x) != EOF)//一直读取数据{if (x > a[0])//大于根节点的进来{a[0] = x;AdjustDown(a, k, 0);}}while (k > 0)//打印结果(升序){printf("%d ", a[0]);swap(&a[0], &a[k - 1]);k--;AdjustDown(a, k, 0);}printf("\n");free(a);
}建测试数据代码:
void CreateNDate()
{// 造数据int n = 10000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i)//10000个随机数{int x = rand() % 1000000;fprintf(fin, "%d\n", x);}for (int i = 9; i >= 0; --i)//造最大的K(10)个数,验证结果{int x = 1000000 + i;fprintf(fin, "%d\n", x);}fclose(fin);
}感谢大家观看= ̄ω ̄=




)
)





)




kotlin依赖报错)


