第一门课：神经网络和深度学习 (Neural Networks and Deep Learning)

第二周：神经网络的编程基础 (Basics of Neural Network programming)

2.1 二分类(Binary Classification)

这周我们将学习神经网络的基础知识，其中需要注意的是，当实现一个神经网络的时候，我们需要知道一些非常重要的技术和技巧。例如有一个包含𝑚个样本的训练集，你很可能习惯于用一个 for 循环来遍历训练集中的每个样本，但是当实现一个神经网络的时候，我们通常不直接使用 for 循环来遍历整个训练集，所以在这周的课程中你将学会如何处理训练集。

另外在神经网络的计算中，通常先有一个叫做前向暂停(forward pause)或叫做前向传播(foward propagation)的步骤，接着有一个叫做反向暂停(backward pause) 或叫做反向传播(backward propagation)的步骤。所以这周我也会向你介绍为什么神经网络的训练过程可以分为前向传播和反向传播两个独立的部分。

在课程中我将使用逻辑回归(logistic regression)来传达这些想法，以使大家能够更加容易地理解这些概念。即使你之前了解过逻辑回归，我认为这里还是有些新的、有趣的东西等着你去发现和了解，所以现在开始进入正题。

逻辑回归是一个用于二分类(binary classification)的算法。首先我们从一个问题开始说起，这里有一个二分类问题的例子，假如你有一张图片作为输入，比如这只猫，如果识别这张图片为猫，则输出标签 1 作为结果；如果识别出不是猫，那么输出标签 0 作为结果。现在我们可以用字母𝑦来表示输出的结果标签，如下图所示：

我们来看看一张图片在计算机中是如何表示的，为了保存一张图片，需要保存三个矩阵，它们分别对应图片中的红、绿、蓝三种颜色通道，如果你的图片大小为 64x64 像素，那么你就有三个规模为 64x64 的矩阵，分别对应图片中红、绿、蓝三种像素的强度值。为了便于表示，这里我画了三个很小的矩阵，注意它们的规模为 5x4 而不是 64x64，如下图所示：

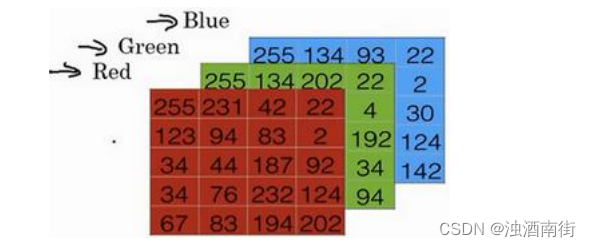
为了把这些像素值放到一个特征向量中，我们需要把这些像素值提取出来，然后放入一个特征向量𝑥。为了把这些像素值转换为特征向量 𝑥，我们需要像下面这样定义一个特征向量 𝑥 来表示这张图片，我们把所有的像素都取出来，例如 255、231 等等，直到取完所有的红色像素，接着最后是 255、134、…、255、134 等等，直到得到一个特征向量，把图片中所有的红、绿、蓝像素值都列出来。如果图片的大小为 64x64 像素，那么向量 𝑥 的总维度，将是 64 乘以 64 乘以 3，这是三个像素矩阵中像素的总量。在这个例子中结果为 12,288。现在我们用𝑛𝑥 = 12,288，来表示输入特征向量的维度，有时候为了简洁，我会直接用小写的𝑛来表示输入特征向量𝑥的维度。所以在二分类问题中，我们的目标就是习得一个分类器，它以图片的特征向量作为输入，然后预测输出结果𝑦为 1 还是 0，也就是预测图片中是否有猫：

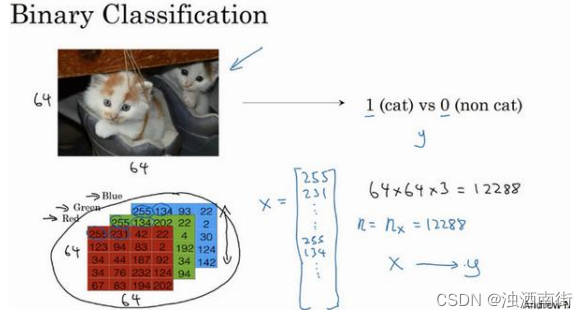
接下来我们说明一些在余下课程中，需要用到的一些符号。
符号定义 ：
𝑥：表示一个𝑛𝑥维数据，为输入数据，维度为(𝑛𝑥, 1)；
𝑦：表示输出结果，取值为(0,1)；
(𝑥(𝑖), 𝑦(𝑖))：表示第𝑖组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据；
𝑋 = [𝑥(1), 𝑥(2), . . . , 𝑥(𝑚)]：表示所有的训练数据集的输入值，放在一个 𝑛𝑥 × 𝑚的矩阵中，其中𝑚表示样本数目;
𝑌 = [𝑦(1), 𝑦(2), . . . , 𝑦(𝑚)]：对应表示所有训练数据集的输出值，维度为1 × 𝑚。

用一对(𝑥, 𝑦)来表示一个单独的样本，𝑥代表𝑛𝑥维的特征向量，𝑦 表示标签(输出结果)只能为 0 或 1。 而训练集将由𝑚个训练样本组成，其中(𝑥(1), 𝑦(1))表示第一个样本的输入和输出，(𝑥(2), 𝑦(2))表示第二个样本的输入和输出，直到最后一个样本(𝑥(𝑚), 𝑦(𝑚))，然后所有的这些一起表示整个训练集。有时候为了强调这是训练样本的个数，会写作𝑀𝑡𝑟𝑎𝑖𝑛，当涉及到测试集的时候，我们会使用𝑀𝑡𝑒𝑠𝑡来表示测试集的样本数。

最后为了能把训练集表示得更紧凑一点，我们会定义一个矩阵用大写𝑋的表示，它由输入向量𝑥(1)、𝑥(2)等组成，如下图放在矩阵的列中，所以现在我们把𝑥(1)作为第一列放在矩阵中，𝑥(2)作为第二列，𝑥(𝑚)放到第𝑚列，然后我们就得到了训练集矩阵𝑋。所以这个矩阵有𝑚列，𝑚是训练集的样本数量，然后这个矩阵的高度记为𝑛𝑥，注意有时候可能因为其他某些原因，矩阵𝑋会由训练样本按照行堆叠起来而不是列，如下图所示：𝑥(1)的转置直到𝑥(𝑚)的转置，但是在实现神经网络的时候，使用左边的这种形式，会让整个实现的过程变得更加简单：

现在来简单温习一下:𝑋是一个规模为𝑛𝑥乘以𝑚的矩阵，当你用 Python 实现的时候，你会看到 X.shape，这是一条 Python 命令，用于显示矩阵的规模，即 X.shape 等于(𝑛𝑥, 𝑚)，𝑋是一个规模为𝑛𝑥乘以𝑚的矩阵。所以综上所述，这就是如何将训练样本（输入向量𝑋的集合）表示为一个矩阵。

那么输出标签𝑦呢？同样的道理，为了能更加容易地实现一个神经网络，将标签𝑦放在列中将会使得后续计算非常方便，所以我们定义大写的𝑌等于𝑦(1), 𝑦(𝑚), . . . , 𝑦(𝑚)，所以在这里是一个规模为 1 乘以𝑚的矩阵，同样地使用 Python 将表示为 Y.shape 等于(1, 𝑚)，表示这是一个规模为 1 乘以𝑚的矩阵。

当你在后面的课程中实现神经网络的时候，你会发现，一个好的符号约定能够将不同训练样本的数据很好地组织起来。而我所说的数据不仅包括 𝑥 或者 𝑦 还包括之后你会看到的其他的量。将不同的训练样本的数据提取出来，然后就像刚刚我们对 𝑥 或者 𝑦 所做的那样，将他们堆叠在矩阵的列中，形成我们之后会在逻辑回归和神经网络上要用到的符号表示。如果有时候你忘了这些符号的意思，比如什么是 𝑚，或者什么是 𝑛，或者忘了其他一些东西，我们也会在课程的网站上放上符号说明，然后你可以快速地查阅每个具体的符号代表什么意思，好了，我们接着到下一个视频，在下个视频中，我们将以逻辑回归作为开始。 备注：附录里也写了符号说明。

2.2 逻辑回归(Logistic Regression)

在这个视频中，我们会重温逻辑回归学习算法，该算法适用于二分类问题，本节将主要介绍逻辑回归的 Hypothesis Function（假设函数）。

对于二元分类问题来讲，给定一个输入特征向量𝑋，它可能对应一张图片，你想识别这张图片识别看它是否是一只猫或者不是一只猫的图片，你想要一个算法能够输出预测，你只能称之为𝑦^ ，也就是你对实际值 𝑦 的估计。更正式地来说，你想让 𝑦^ 表示 𝑦 等于 1 的一种可能性或者是机会，前提条件是给定了输入特征𝑋。换句话来说，如果𝑋是我们在上个视频看到的图片，你想让 𝑦^ 来告诉你这是一只猫的图片的机率有多大。在之前的视频中所说的，𝑋是一个𝑛𝑥维的向量（相当于有𝑛𝑥个特征的特征向量）。我们用𝑤来表示逻辑回归的参数，这也是一个𝑛𝑥维向量（因为𝑤实际上是特征权重，维度与特征向量相同），参数里面还有𝑏，这是一个实数（表示偏差）。所以给出输入𝑥以及参数𝑤和𝑏之后，我们怎样产生输出预测值𝑦^ ，一件你可以尝试却不可行的事是让 𝑦^ = $w^{T}x+b$。

这时候我们得到的是一个关于输入𝑥的线性函数，实际上这是你在做线性回归时所用到的，但是这对于二元分类问题来讲不是一个非常好的算法，因为你想让𝑦^ 表示实际值𝑦等于 1的机率的话，𝑦^ 应该在 0 到 1 之间。这是一个需要解决的问题，因为$w^{T}x+b$可能比 1 要大得多，或者甚至为一个负值。对于你想要的在 0 和 1 之间的概率来说它是没有意义的，因此在逻辑回归中，我们的输出应该是𝑦^等于由上面得到的线性函数式子作为自变量的 sigmoid函数中，公式如上图最下面所示，将线性函数转换为非线性函数。

下图是 sigmoid 函数的图像，如果我把水平轴作为𝑧轴，那么关于𝑧的 sigmoid 函数是这样的，它是平滑地从 0 走向 1，让我在这里标记纵轴，这是 0，曲线与纵轴相交的截距是 0.5，这就是关于𝑧的 sigmoid 函数的图像。我们通常都使用𝑧来表示$w^{T}x+b$的值。

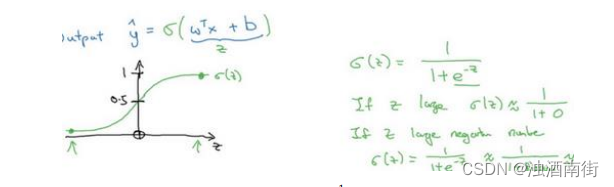
关于 sigmoid 函数的公式是这样的，𝜎(𝑧) =$\frac{1}{1+e^{-z}}$，在这里𝑧是一个实数，这里要说明一些要注意的事情，如果𝑧非常大那么$e^{-z}$将会接近于 0，关于𝑧的 sigmoid 函数将会近似等于 1 除以 1 加上某个非常接近于 0 的项，因为𝑒 的指数如果是个绝对值很大的负数的话，这项将会接近于 0，所以如果𝑧很大的话那么关于𝑧的 sigmoid 函数会非常接近 1。相反地，如果𝑧非常小或者说是一个绝对值很大的负数，那么关于$e^{-z}$这项会变成一个很大的数，你可以认为这是 1 除以 1 加上一个非常非常大的数，所以这个就接近于 0。实际上你看到当𝑧变成一个绝对值很大的负数，关于𝑧的 sigmoid 函数就会非常接近于 0，因此当你实现逻辑回归时，你的工作就是去让机器学习参数𝑤以及𝑏这样才使得𝑦^成为对𝑦 = 1这一情况的概率的一个很好的估计。

在继续进行下一步之前，介绍一种符号惯例，可以让参数𝑤和参数𝑏分开。在符号上要注意的一点是当我们对神经网络进行编程时经常会让参数𝑤和参数𝑏分开，在这里参数𝑏对应的是一种偏置。在之前的机器学习课程里，你可能已经见过处理这个问题时的其他符号表示。比如在某些例子里，你定义一个额外的特征称之为$x_0$，并且使它等于 1，那么现在𝑋就是一个𝑛𝑥加 1 维的变量，然后你定义𝑦^ = 𝜎(${\theta }^{T}x$)的 sigmoid 函数。在这个备选的符号惯例里，你有一个参数向量$\theta 0,\theta 1,\theta 2,...,{\theta }_{nx}$，这样θ0就充当了𝑏，这是一个实数，而剩下的θ1 直到${\theta }_{nx}$充当了𝑤，结果就是当你实现你的神经网络时，有一个比较简单的方法是保持𝑏和𝑤分开。但是在这节课里我们不会使用任何这类符号惯例，所以不用去担心。 现在你已经知道逻辑回归模型是什么样子了，下一步要做的是训练参数𝑤和参数𝑏，你需要定义一个代价函数，让我们在下节课里对其进行解释。

2.3 逻辑回归的代价函数（Logistic Regression Cost Function）

在上个视频中，我们讲了逻辑回归模型，这个视频里，我们讲逻辑回归的代价函数（也翻译作成本函数）。

为什么需要代价函数：
为了训练逻辑回归模型的参数参数𝑤和参数𝑏我们，需要一个代价函数，通过训练代价函数来得到参数𝑤和参数𝑏。先看一下逻辑回归的输出函数：

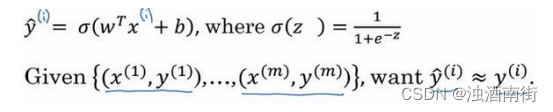
为了让模型通过学习调整参数，你需要给予一个𝑚样本的训练集，这会让你在训练集上找到参数𝑤和参数𝑏,，来得到你的输出。

对训练集的预测值，我们将它写成$\hat{y}$，我们更希望它会接近于训练集中的y值，为了对上面的公式更详细的介绍，我们需要说明上面的定义是对一个训练样本来说的，这种形式也使用于每个训练样本，我们使用这些带有圆括号的上标来区分索引和样本，训练样本i所对应的预测值是y(i),是用训练样本的$w^{T}x(i)+b$然后通过 sigmoid 函数来得到，也可以把𝑧定义为$z(i)=w^{T}x(i)+b$,我们将使用这个符号(i)注解，上标(i)来指明数据表示x或者y或者z或者其他数据的第𝑖个训练样本，这就是上标(i)的含义。

损失函数：

损失函数又叫做误差函数，用来衡量算法的运行情况，$Lossfunction:L(\hat{y},y)$.
我们通过这个𝐿称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我们在逻辑回归模型中会定义另外一个损失函数。

我们在逻辑回归中用到的损失函数是：$L(\hat{y},y)=-ylog(\hat{y})-(1-y)log(1-\hat{y})$
为什么要用这个函数作为逻辑损失函数？当我们使用平方误差作为损失函数的时候，你会想要让这个误差尽可能地小，对于这个逻辑回归损失函数，我们也想让它尽可能地小，为了更好地理解这个损失函数怎么起作用，我们举两个例子:

当𝑦 = 1时损失函数$L=-log(\hat{y})$，如果想要损失函数𝐿尽可能得小，那么$\hat{y}$就要尽可能大，因为 sigmoid 函数取值[0,1]，所以$\hat{y}$会无限接近于 1。
当𝑦 = 0时损失函数$L=-log(1-\hat{y})$，如果想要损失函数𝐿尽可能得小，那么$\hat{y}$就要尽可能小，因为 sigmoid 函数取值[0,1]，所以$\hat{y}$会无限接近于 0。

在这门课中有很多的函数效果和现在这个类似，就是如果𝑦等于 1，我们就尽可能让$\hat{y}$变大，如果𝑦等于 0，我们就尽可能让$\hat{y}$ 变小。 损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对𝑚个样本的损失函数求和然后除以𝑚:
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=\frac{1}{m}\sum _{i=1}^m(-y^{(i)}\log ({\hat{y}}^{(i)})-(1-y^{(i)})\log (1-{\hat{y}}^{(i)}))$$

损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的𝑤和𝑏，来让代价函数 𝐽 的总代价降到最低。 根据我们对逻辑回归算法的推导及对单个样本的损失函数的推导和针对算法所选用参数的总代价函数的推导，结果表明逻辑回归可以看做是一个非常小的神经网络，在下一个视频中，我们会看到神经网络会做什么。

2.4 梯度下降法（Gradient Descent）

梯度下降法可以做什么？
在你测试集上，通过最小化代价函数（成本函数）𝐽(𝑤, 𝑏)来训练的参数𝑤和𝑏，

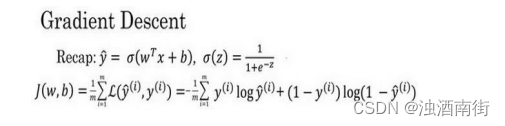
如图，在第二行给出和之前一样的逻辑回归算法的代价函数（成本函数）,梯度下降法的形象化说明

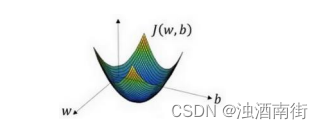
在这个图中，横轴表示你的空间参数𝑤和𝑏，在实践中，𝑤可以是更高的维度，但是为了更好地绘图，我们定义𝑤和𝑏，都是单一实数，代价函数（成本函数）𝐽(𝑤, 𝑏)是在水平轴𝑤和𝑏上的曲面，因此曲面的高度就是𝐽(𝑤, 𝑏)在某一点的函数值。我们所做的就是找到使得代价函数（成本函数）𝐽(𝑤, 𝑏)函数值是最小值，对应的参数𝑤和𝑏。

如图，代价函数（成本函数）𝐽(𝑤, 𝑏)是一个凸函数(convex function)，像一个大碗一样。

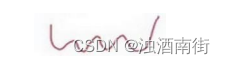
如图，这就与刚才的图有些相反，因为它是非凸的并且有很多不同的局部最小值。由于逻辑回归的代价函数（成本函数）𝐽(𝑤, 𝑏)特性，我们必须定义代价函数（成本函数）𝐽(𝑤, 𝑏)为凸函数。 初始化𝑤和𝑏，可以用如图那个小红点来初始化参数𝑤和𝑏，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。

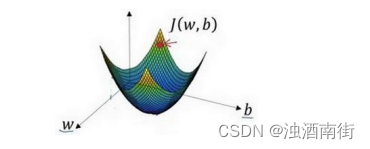
我们以如图的小红点的坐标来初始化参数𝑤和𝑏。
2. 朝最陡的下坡方向走一步，不断地迭代,我们朝最陡的下坡方向走一步，如图，走到了如图中第二个小红点处。我们可能停在这里也有可能继续朝最陡的下坡方向再走一步，如图，经过两次迭代走到第三个小红点处。

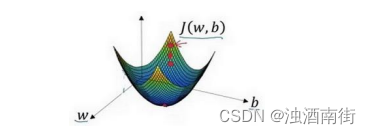
3.直到走到全局最优解或者接近全局最优解的地方通过以上的三个步骤我们可以找到全局最优解，也就是代价函数（成本函数）𝐽(𝑤, 𝑏)这
个凸函数的最小值点。梯度下降法的细节化说明（仅有一个参数）

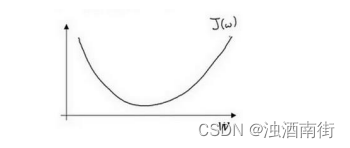
假定代价函数（成本函数）𝐽(𝑤) 只有一个参数𝑤，即用一维曲线代替多维曲线，这样可以更好画出图像。
$$w:=w-\alpha \frac{dJ(w)}{dw}$$

迭代就是不断重复做如图的公式:

=表示更新参数,
𝑎 表示学习率（learning rate），用来控制步长（step），即向下走一步的长度𝑑𝐽(𝑤)𝑑𝑤就是函数𝐽(𝑤)对𝑤 求导（derivative），在代码中我们会使用𝑑𝑤表示这个结果

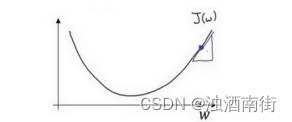
对于导数更加形象化的理解就是斜率（slope），如图该点的导数就是这个点相切于 𝐽(𝑤)的小三角形的高除宽。假设我们以如图点为初始化点，该点处的斜率的符号是正的，即𝑑𝐽(𝑤)/𝑑𝑤> 0，所以接下来会向左走一步。

整个梯度下降法的迭代过程就是不断地向左走，直至逼近最小值点。

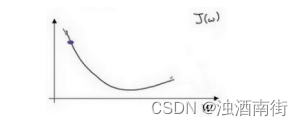
假设我们以如图点为初始化点，该点处的斜率的符号是负的，即𝑑𝐽(𝑤)/𝑑𝑤< 0，所以接下来会向右走一步。

整个梯度下降法的迭代过程就是不断地向右走，即朝着最小值点方向走。
梯度下降法的细节化说明（两个参数）
逻辑回归的代价函数（成本函数）𝐽(𝑤, 𝑏)是含有两个参数的。
$$w:=w-\alpha \frac{\partial J(w,b)}{\partial w}$$
$$b:=b-\alpha \frac{\partial J(w,b)}{\partial w}$$

𝜕 表示求偏导符号，可以读作 round，𝜕𝐽(𝑤,𝑏)/𝜕𝑤 就是函数𝐽(𝑤, 𝑏) 对𝑤 求偏导，在代码中我们会使用𝑑𝑤 表示这个结果， 𝜕𝐽(𝑤,𝑏)/𝜕𝑏 就是函数𝐽(𝑤, 𝑏)对𝑏 求偏导，在代码中我们会使用𝑑𝑏 表示这个结果， 小写字母𝑑 用在求导数（derivative），即函数只有一个参数， 偏导数符号𝜕 用在求偏导（partial derivative），即函数含有两个以上的参数。