完整报告链接：http://tecdat.cn/?p=28579

作者：Nuo Liu

数据变得越来越重要，其核心应用“预测”也成为互联网行业以及产业变革的重要力量。近年来网络 P2P借贷发展形势迅猛，一方面普通用户可以更加灵活、便快捷地获得中小额度的贷款，另一方面由于相当多数量用户出现违约问题而给 P2P信贷平台以及借贷双方带来诸多纠纷，因此根据用户历史款情况准确预测潜在是否还会发生违约就非常有必要（点击文末“阅读原文”获取完整报告数据）。

相关视频

解决方案

任务/目标

对于用户贷款数据（查看文末了解数据免费获取方式）是否违约的预测，结果解释。

数据源准备

删除属性

删除数据集中与建立决策树无关的属性IDX、Listinginfo，此类属性作为用户标记/日期标记作用，与借款人信贷违约明显无关。

删除数据集中distinct为1的属性webloginfo\_10、Education\_info7、webloginfo_49，此类属性仅存在同一个数值，对分类结果无影响。

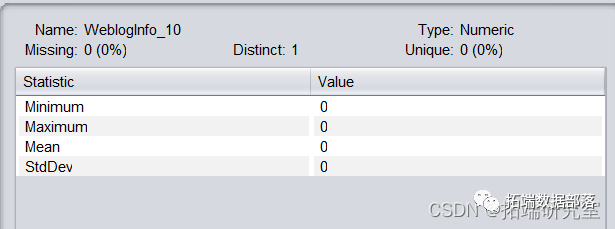
webloginfo_10属性描述，其他属性类似

缺失值处理

缺失值情况如下表，按缺失值比例由大到小排列

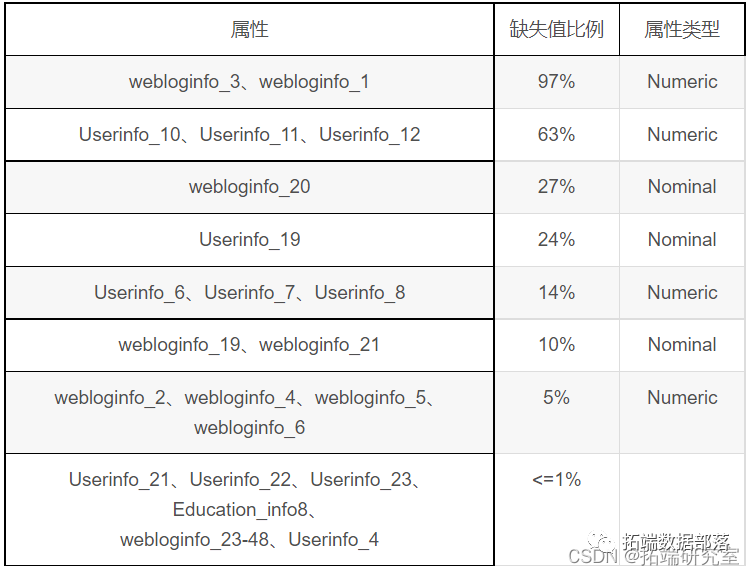
对于属性webloginfo\_3、webloginfo\_1，由于缺失值比例过大，直接删除两属性。操作步骤为预处理界面勾选两属性，点击Remove。

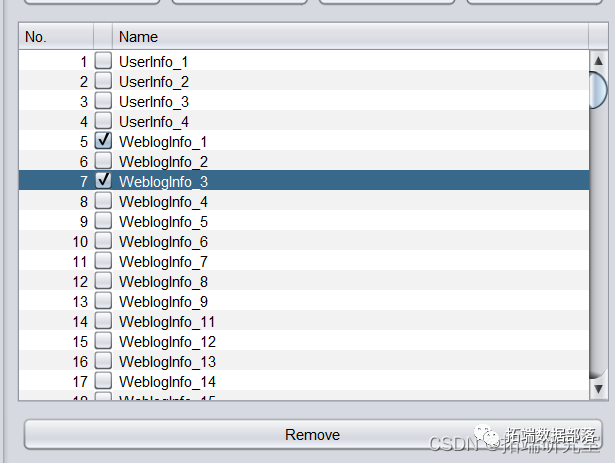
对于属性Userinfo\_21、Userinfo\_22、Userinfo\_23、Education\_info8、webloginfo\_23-48、Userinfo\_4，由于缺失值比例较小，不足1%。webloginfo\_2、webloginfo\_4、webloginfo\_5、webloginfo\_6缺失值比例为5%。因此直接删除缺失值对应instance，以删除Userinfo_21中的缺失值为例，操作步骤如下：

删除后，剩余19200条实例如下，数据集损失的实例数不足5%，认为对后续决策树建立没有影响。

对于其他缺失值属性，若为Numeric属性，用平均值代替缺失值，若为Nominal属性，用它的众数来代替缺失值。选择 weka中“ReplaceMissingValues"过滤器进行实现

处理后检查不存在缺失值，至此缺失值处理完成。

Numeric 属性离散化处理

使用“NumerictoNominal”过滤器实现Numeric属性的离散化，为方便处理使用MultiFilter对所有Numeric属性进行操作。

处理后如图，所有Numeric属性均已变为Nominal属性。

特征转换

特征理解

该数据集数据来源于中国一家著名的P2P公司的借款记录。数据集中包括借款人的ID、日期、借款人特征（地点、婚姻状态等信息）、网络行为、学历以及第三方数据等全面信息。

Weblog Info_:Info网络行为字段描述使用网络次数多少，:使用第三方数据时间N字段描述第三方数据时间长短。观察发现ThirdParty_ Info\_PeriodN\_属性数据不同维度上的特征的尺度不一致，需要进行标准化处理

特征提升

按照第一次方法，对数据集进行缺失值删补，步骤省略。

将ThirdParty字段属性标准化，在预处理界面选用unsupervised. attribute. Standardize，标准化给定数据集中所有数值属性的值到一个0均值和单位方差的正态分布。

特征选择

原数据集包含属性较多，为方便后续操作先对数据集进行特征选择处理。

删除数据集中与建立决策树无关的属性IDX、Listinginfo，此类属性作为用户标记/日期标记作用，与借款人信贷违约明显无关。删除数据集中distinct为1的属性webloginfo\_10、Education\_info7、webloginfo_49，此类属性仅存在同一个数值，对分类结果无影响。

在预处理界面选择AttributeSelection过滤器，选择CfsSubsetEval评估器，选择BestFirst 搜索方法。最终得到除target之外的74个属性。

特征降维

由于ThirdParty_ Info\_PeriodN\_为使用第三方数据时间N字段，描述不同阶段使用时间长短，WeblogInfo字段为使用网络次数。根据意义判断，同时包含同类别不同阶段数据不太合理，因此运用主成分分析方法将ThirdParty_ Info\_PeriodN\_属性合并成为一个综合指标，选择排名第一的属性命名为ThirdParty属性，替换原数据集中所有ThirdParty_ Info\_PeriodN\_*变量。同理对WeblogInfo字段使用主成分分析方法进行合并与替换。

以WeblogInfo降维为例，设置提取5个维度作为主成分，排序后得到第一条属性的个体评价最高达到0.9388，保留第一条属性，导出引入数据集，命名为WeblogInfo。ThirdParty字段同理。

特征构造

经过选择后包含的属性中，User2、4、6、7、18、19均为地点属性，且包含300余条distinct，对决策树造成干扰。而其中User6、7；User18、19分别为同一地点的省份与城市名称，存在信息冗余，因此首先对这几类地点属性进行处理。

再抽样与离散化

• 对类属性target进行离散化，过程省略

• 第一次处理时并没有对target之外的Numeric属性进行离散化处理，导致决策树同一个属性在多个节点出现。因此为降低树深度，对其他Numeric属性进行离散化处理。首先观察user16、Education1、Education5、Movement属性为布尔变量。Socialwork7属性只包含-1，0，1三个值，将以上属性直接转换为Nominal属性。

其次对其他数值型属性进行离散化。在预处理界面选择Discretize，根据第一次作业结果判断，设置bins为3，分类区间取小数点后两位。

• 再抽样。target属性中发现Lable为1（即存在违约风险）的频数较小。为防止进行分类建模时学习不到小类特征，运用SMOTE包增加小类数量，加大小类比例，以便后续机器学习。设置参数percentage为800%，实例数量扩大为原来的8倍。为防止抽样范围过小造成数据与原数据比例失衡，设置nearestNeighbors为100.

运行后如图所示，实例数量增加到33320条。

至此预处理完毕，对训练集与测试集进行同样处理，为避免测试集与训练集不匹配问题，用记事本打开测试集.arff文件修改表头至与训练集一致。

建模和模型优化

随机森林

Weka操作

打开预处理后的训练集，在classifier模块中选择CVParameterSelection，并选择RandomForest决策分类树算法，寻找最佳参数。

在经过处理后的测试集上进行测试，在more options中选择cost sensitive，并将左下至右上对角线上数值均设为1。

运行结果如下：

模型正确率为85.3684%，召回率为0.854，假阳性数量较大。以借款金额每人1000，中介收费率为0.3计算ROI，结果为450000。

将cost sensitive改变为只有左下数值为1，进行再次运行，得出结果相同。

为了取得最优ROI，使用最小化代价函数CostsensitiveClassifier，并将参数minimize expected cost设置为True，cost sensitive设置为只有左下角为1。

结果显示为：

可以看出假阳性数值明显减少，但是模型正确率和召回率严重下降，且由于真阳性也减少，ROI降低为172800。

因此随机森林算法中，ROI最大为450000。

支持向量机SVM算法

算法原理

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。

Weka操作

在package manager中下载LibSVM包，并在classifier模块中选择最优参数选择CVParameterSelection，使用SVM分类算法。

同时调整cost sensitive为左下至右上数值均为1，得出结果为：

模型正确率为79.7725%，召回率为0.798，混淆矩阵中假阳性仍然很多，ROI数值为623100。修改cost sensitive为只有左下数值为1时，结果相同。

使用最小化代价函数CostsensitiveClassifier，并将参数minimize expected cost设置为True，cost sensitive设置为左下至右上数值均为1时，结果如下：

相比最优参数选择构建的模型，正确率略下降为79.281%，召回率为0.793，ROI数值为616800，同样小于最优参数构建模型。

因此SVM分类算法最大ROI为623100。

将test和train两个数据集中的target变量从数字型转化为名义型

CART

原理：

C4.5中模型是用较为复杂的熵来度量，使用了相对较为复杂的多叉树，只能处理分类不能处理回归。对这些问题，CART(Classification And Regression Tree)做了改进，可以处理分类，也可以处理回归。

1. CART分类树算法的最优特征选择方法

ID3中使用了信息增益选择特征，增益大优先选择。C4.5中，采用信息增益比选择特征，减少因特征值多导致信息增益大的问题。CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（比）相反。

假设K个类别，第k个类别的概率为pk，概率分布的基尼系数表达式：

如果是二分类问题，第一个样本输出概率为p，概率分布的基尼系数表达式为：

对于样本D，个数为|D|，假设K个类别，第k个类别的数量为|Ck|，则样本D的基尼系数表达式：

对于样本D，个数为|D|，根据特征A的某个值a，把D分成|D1|和|D2|，则在特征A的条件下，样本D的基尼系数表达式为：

比较基尼系数和熵模型的表达式，二次运算比对数简单很多。尤其是二分类问题，更加简单。

和熵模型的度量方式比，基尼系数对应的误差有多大呢？对于二类分类，基尼系数和熵之半的曲线如下：

基尼系数和熵之半的曲线非常接近，因此，基尼系数可以做为熵模型的一个近似替代。

CART分类树算法每次仅对某个特征的值进行二分，而不是多分，这样CART分类树算法建立起来的是二叉树，而不是多叉树。

CART分类树算法具体流程

CART分类树建立算法流程，之所以加上建立，是因为CART分类树算法有剪枝算法流程。

算法输入训练集D，基尼系数的阈值，样本个数阈值。

输出的是决策树T。

算法从根节点开始，用训练集递归建立CART分类树。

(1)对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归。

(2)计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

(3)计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和C4.5算法里描述的相同。

(4)在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2。

(5)对左右的子节点递归的调用1-4步，生成决策树。

对生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

CART算法缺点：

(1) 无论ID3，C4.5，CART都是选择一个最优的特征做分类决策，但大多数，分类决策不是由某一个特征决定，而是一组特征。这样得到的决策树更加准确，这种决策树叫多变量决策树(multi-variate decision tree)。在选择最优特征的时，多变量决策树不是选择某一个最优特征，而是选择一个最优的特征线性组合做决策。代表算法OC1。

(2) 样本一点点改动，树结构剧烈改变。这个通过集成学习里面的随机森林之类的方法解决。

Weka操作

运行结果如下：

模型正确率为84.3148%，识别率=召回率=0.843，F-Measure=0.835。

以借款金额每人1000，中介收费率为0.3计算ROI，结果为294100。

将useprune改为False，即不剪枝，运行结果如下：

模型正确率为83.2124%，识别率=召回率=0.832，F-Measure=0.826。

以借款金额每人1000，中介收费率为0.3计算ROI，结果为327900。

对比剪枝结果，发现各项指标剪枝优于不剪枝，而不剪枝的ROI大于剪枝的模型。

调整矩阵：

输出结果中，混淆矩阵相同。

为了取得最优ROI，使用最小化代价函数CostsensitiveClassifier，并将参数minimize expected cost设置为True，cost sensitive设置为只有左下角为1。simpleCART选择不剪枝。

输出结果如下：

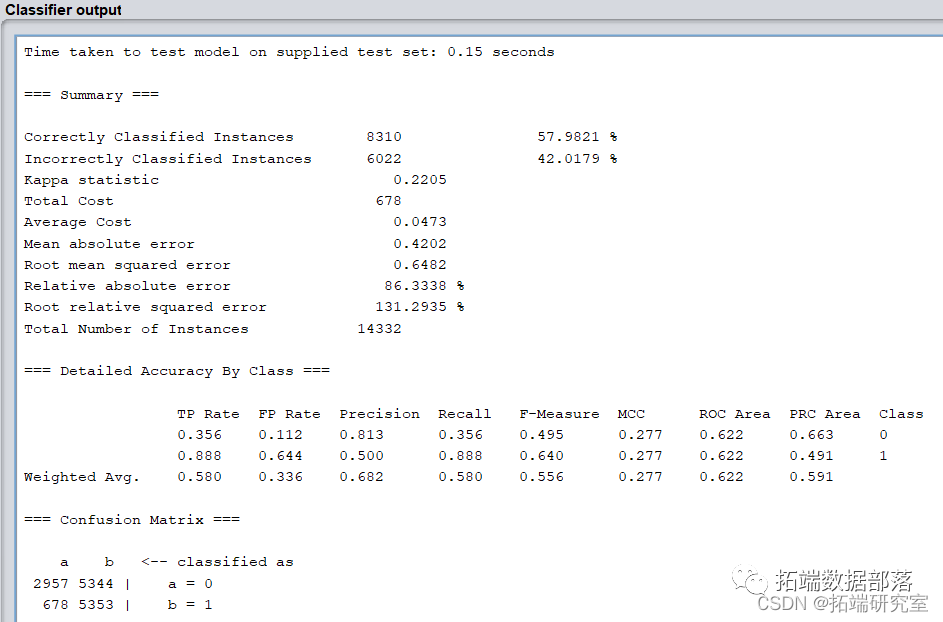
模型正确率和召回率严重下降，ROI降低为209100。

因此simpleCART算法中，ROI最大为327900。

Naivebayes 朴素贝叶斯

朴素贝叶斯算法

朴素贝叶斯算法（Naive Bayesian algorithm) 是应用最为广泛的分类算法之一。

朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重，也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。

优缺点：

优点

朴素贝叶斯算法假设了数据集属性之间是相互独立的，因此算法的逻辑性十分简单，并且算法较为稳定，当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。

缺点

属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的，因为数据集的属性之间往往都存在着相互关联，如果在分类过程中出现这种问题，会导致分类的效果大大降低。

Weka操作过程

打开预处理后的训练集，在classifier模块中选择CVParameterSelection，并选择simpleCART决策分类树算法，寻找最佳参数。

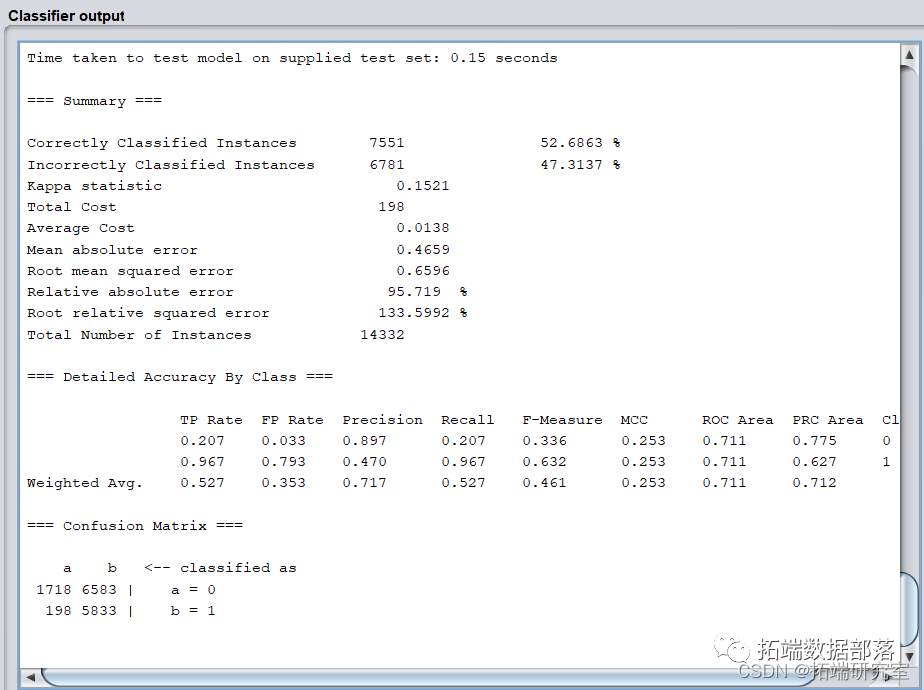
模型的正确率仅52.6863%，识别率=召回率=0.527，F-Measure=0.467，模型各项指标很差，而且模型不稳定。

以借款金额每人1000，中介收费率为0.3计算ROI，结果为317400。

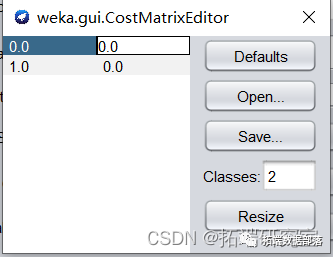
输出结果如下：

模型正确率和召回率严重下降，ROI降低为0。

因此naivebayes算法中，ROI最大为317400。

而观测各项指标结果，以及bayes适用范围可以判断，该数据集不适合使用bayes算法。

ID3

weka操作

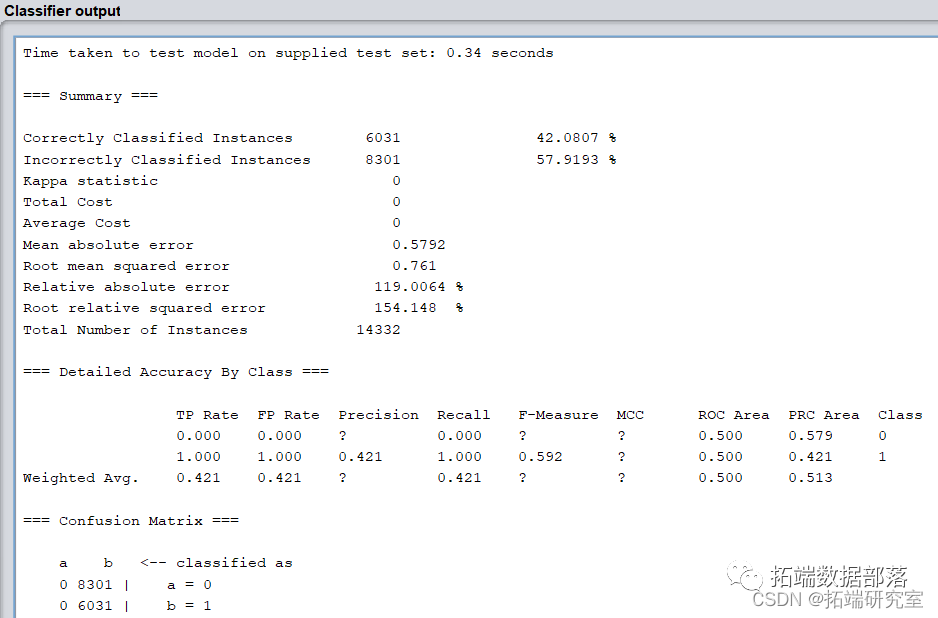
相同步骤，target名义变量设置，cost sensitive 设置，将假阳性错误的代价敏感度提高，选择ID3算法，结果如下，Recall 为75.2%，ROI 为1550000。

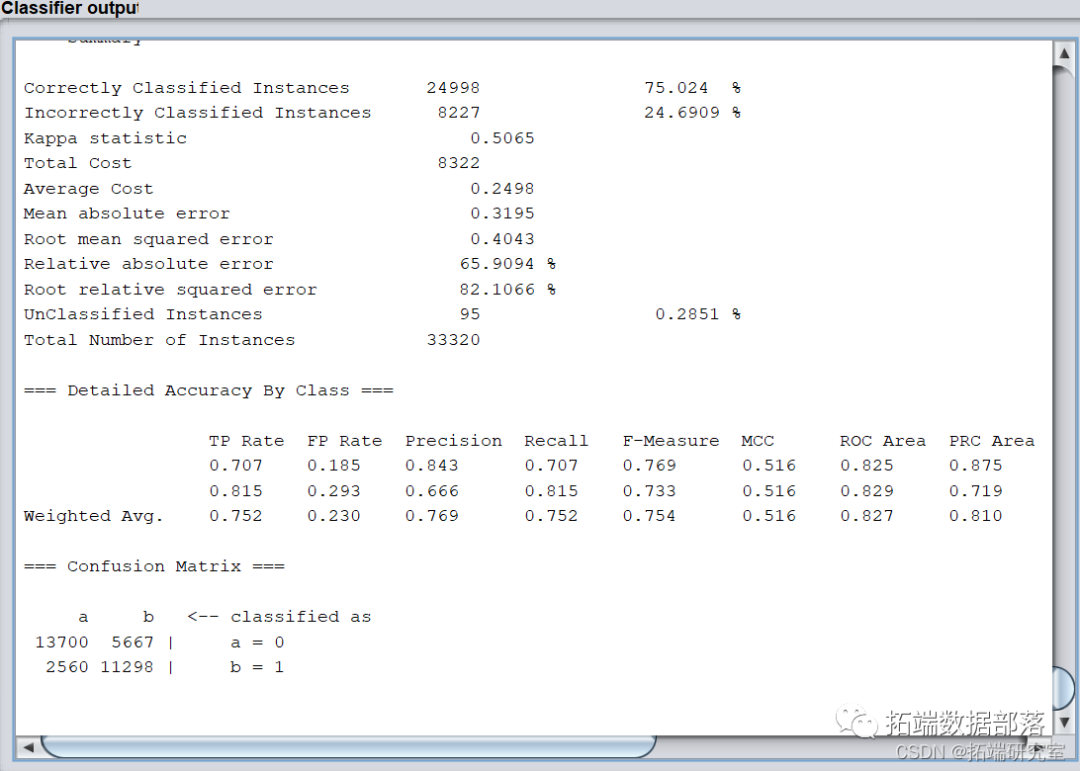
J48算法

J48流程

（1）使用经过预处理的数据集，使用 CVParameterSelection 中的classifier中的Tree-J48并调整和寻找最佳参数，在test option中选择 Supplied test set 并上传预处理完成的测试集：

在经过处理后的测试集上进行测试，在more options中选择cost sensitive，并将左下至右上对角线上数值均设为1。

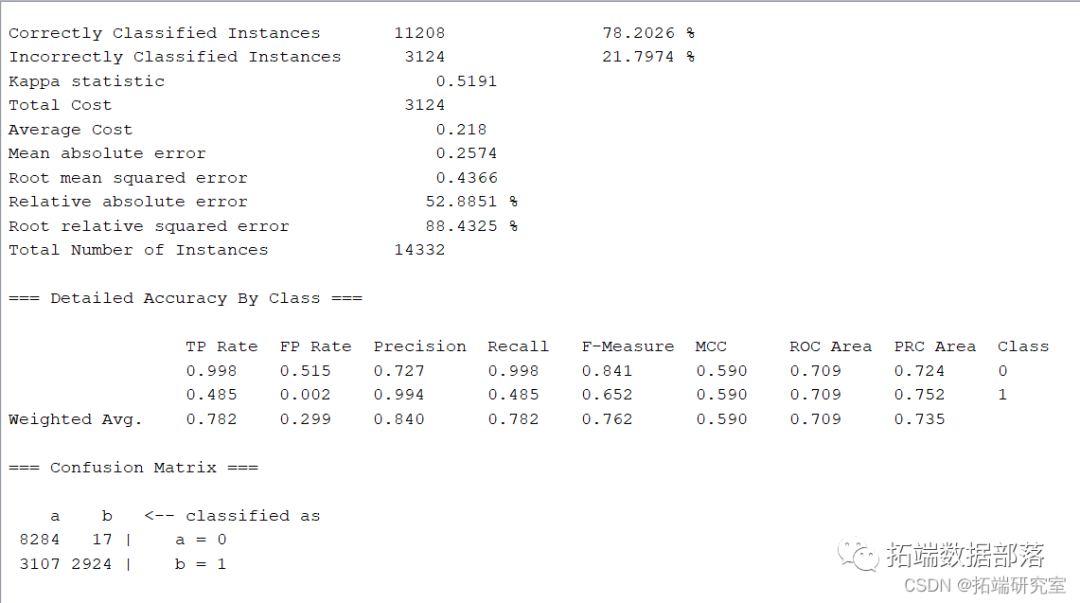
模型正确率为78.2026%，召回率为0.782。此时以借款金额每人1000，中介收费率为0.3计算ROI，结果为-621800。

为了取得最优ROI，使用最小化代价函数CostsensitiveClassifier，并将参数minimize expected cost设置为True，cost sensitive设置为只有左下角为1。

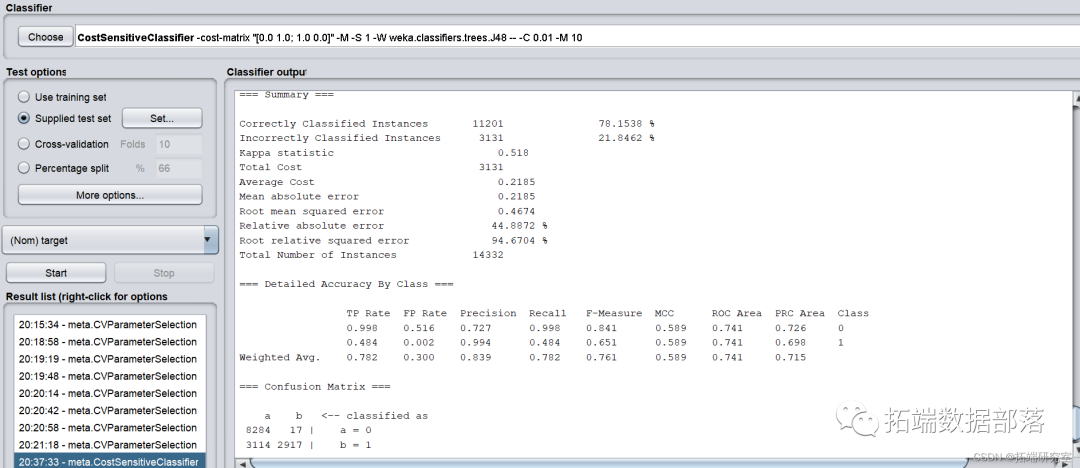
模型正确率和召回率略微下降， ROI降低为-628800.

因此J48算法中，当使用目前的参数时ROI最大为-621800。

Simple logistic

Simple logistic 流程

使用经过预处理的数据集，使用 CVParameterSelection 中的classifier中的Functions-SimpleLogistic并调整参数，在test option中选择 Supplied test set 并上传预处理完成的测试集：

正确率为61.1917%，召回率为0.612。此时以借款金额每人1000，中介收费率为0.3计算ROI，结果为-1223700。

为了取得最优ROI，使用最小化代价函数CostsensitiveClassifier，并将参数minimize expected cost设置为True，cost sensitive设置为只有左下角为1。

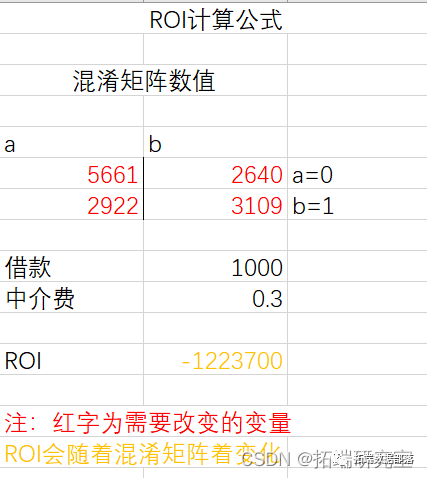
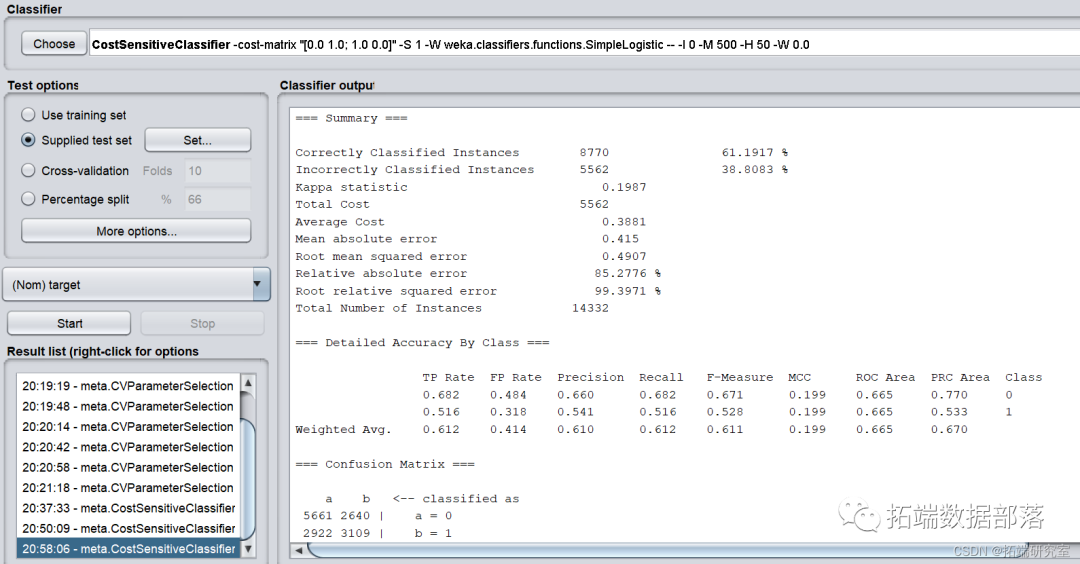
模型正确率和召回率并无波动。因此Simple Logistic算法中，当使用目前的参数时ROI最大为-1223700。

项目结果 

具体结果已经在各个模型后展示，随机森林和支持向量机算法预测应用效果良好。

评估效果不能只看销量，要综合考虑，需要参考业务对接，预测精度，模型可解释性，预测结果仅作为参考一个权重值，还需要专家意见，按照一定的权重来计算。

关于作者

在此对Nuo Liu对本文所作的贡献表示诚挚感谢，她专长深度学习、聚类、分类、回归、社交网络、关联分析。

---

数据获取

在公众号后台回复“信贷数据”，可免费获取完整数据。

 

点击文末“阅读原文”

获取全文完整文档、数据资料。

本文选自《数据分享|WEKA用决策树、随机森林、支持向量机SVM、朴素贝叶斯、逻辑回归信贷违约预测报告》。

本文中的数据和完整报告WORD文档分享到会员群，扫描下面二维码即可加群！

点击标题查阅往期内容

数据分享|Python信贷风控模型：Adaboost,XGBoost,SGD, SVC,随机森林, KNN预测信贷违约支付

Python进行多输出（多因变量）回归：集成学习梯度提升决策树GRADIENT BOOSTING,GBR回归训练和预测可视化

Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析

PYTHON集成机器学习：用ADABOOST、决策树、逻辑回归集成模型分类和回归和网格搜索超参数优化

R语言集成模型：提升树boosting、随机森林、约束最小二乘法加权平均模型融合分析时间序列数据

Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析

R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化

R语言基于树的方法：决策树，随机森林，Bagging，增强树

R语言用逻辑回归、决策树和随机森林对信贷数据集进行分类预测

spss modeler用决策树神经网络预测ST的股票

R语言中使用线性模型、回归决策树自动组合特征因子水平

R语言中自编基尼系数的CART回归决策树的实现

R语言用rle，svm和rpart决策树进行时间序列预测

python在Scikit-learn中用决策树和随机森林预测NBA获胜者

python中使用scikit-learn和pandas决策树进行iris鸢尾花数据分类建模和交叉验证

R语言里的非线性模型：多项式回归、局部样条、平滑样条、 广义相加模型GAM分析

R语言用标准最小二乘OLS，广义相加模型GAM ，样条函数进行逻辑回归LOGISTIC分类

R语言ISLR工资数据进行多项式回归和样条回归分析

R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型

R语言用泊松Poisson回归、GAM样条曲线模型预测骑自行车者的数量

R语言分位数回归、GAM样条曲线、指数平滑和SARIMA对电力负荷时间序列预测

R语言样条曲线、决策树、Adaboost、梯度提升(GBM)算法进行回归、分类和动态可视化

如何用R语言在机器学习中建立集成模型？

R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

在python 深度学习Keras中计算神经网络集成模型

R语言ARIMA集成模型预测时间序列分析

R语言基于Bagging分类的逻辑回归(Logistic Regression)、决策树、森林分析心脏病患者

R语言基于树的方法：决策树，随机森林，Bagging，增强树

R语言基于Bootstrap的线性回归预测置信区间估计方法

R语言使用bootstrap和增量法计算广义线性模型（GLM）预测置信区间

R语言样条曲线、决策树、Adaboost、梯度提升(GBM)算法进行回归、分类和动态可视化

Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析

R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析

R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化

Matlab建立SVM，KNN和朴素贝叶斯模型分类绘制ROC曲线

matlab使用分位数随机森林（QRF）回归树检测异常值