上一期中，我们了解到了堆，堆的结构也可以叫做二叉树的顺序结构，今天我们一起来看看二叉树的链式结构，我们还要学习有关于二叉树递归的书写。
首先，这是一个二叉树，但是对于普通的二叉树来说，增删查改是没有什么价值的。
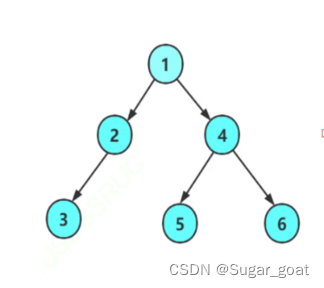
所以那什么才是有价值的呢？
链式二叉树的结构：
我们来看看二叉树的几种遍历：
我们要怎么实现呢？？
我们先来了解以下递归，递归是将一个大问题分解为若干个相似的子问题，同时我们在执行的过程中，要不断接近问题结束的条件。
以前序遍历举例，我们先访问根节点，再进入左子树，进入左子树后访问当前的根节点，也就是左子树，之后以此类推，不断向下访问，结束的调节就是访问到空。
我们可以画图来观察递归调用的结果。
那么中序遍历就是将打印的步骤放在进入左子树后
解决完这个问题后，我们再来解决：如何计算二叉树结点个数的问题
同样的我们也需要使用递归的方式来实现
我们先来思考我们怎样计数：我们可以仿造先序遍历的方式，进入一个结点就+1，但是我们计数的工具是什么呢？？？
我们先来看看这种思路
这里他提供了一个静态的变量size来存储个数，但是我们会发现size在定义之后就无法改变，除非我们每一次调用结束后手动将它置为0，所以这是有问题的 。
下面是正确的写法
我们来看看思路：首先我们先判断这个结点是否为空，为空就返回0，不为空就先往左子树走，左子树为空就向右子树走，都为空就是1个结点，即当前结点加1，一次类推，只要结点不为空，最后都会加1 ，最后计算的结果就是结点个数的和
下面我们试着来思考：如何利用递归求叶子结点个数？？？
我们先来思考：什么是叶子结点？
我们要明确的是，叶子结点就是左右子树都为空的结点，那么我们的思路就明了了，一种特殊的结点，当结点为空就返回0。
第四个问题：如何计算二叉树的高度
我们先来看一个二叉树
它的右子树的高度明显比左子树的高度高。
这里就提示我们左右子树的高度是不一样的，我们要分别记录两个子树的高度，高度是最大的高度，也就是左子树和右子树的高度我们要取最大值。
我们先来看一种错误的写法：
这种写法我们递归返回的时候会重复进行对底层的调用，因为我们不记得左子树和右子树高度的值
正确的方式我们要将这个函数的返回值利用起来，分别记录左右子树高度，
第五题： 计算第k层结点的个数
谢谢观看，希望对大家有所帮助！！！
