文章目录
- 一、线性回归的基本原理
- 1.相关与回归
- 2.线性回归的原理分析
- ①线性回归的一般公式
- ②线性回归的损失函数
- ③线性回归方程的参数求解方法
- A.最小二乘法
- B.梯度下降法
一、线性回归的基本原理
1.相关与回归
相关描述的是变量之间的一种关系。
从统计角度看,变量之间的关系有函数关系和相关关系两种。
函数关系:即当一个或多个变量取一定值时,另一个变量有唯一确定值与之对应。
在实际生活中,有些变量之间并不像函数关系那样,有明确的关系,但又的确存在一定的关系。
例如,二手房的房价与面积,这两个变量之间不存在完全确定的关系,但却存在一定的趋势,即面积会对房价有一定影响,但又存在很大的不确定性。。
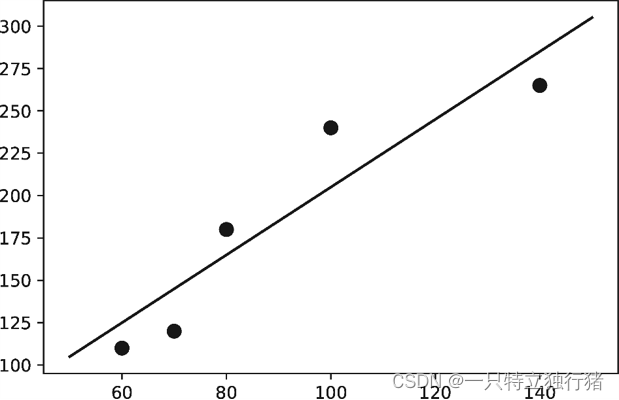
通常把变量之间的这种不确定的相互依存关系称为相关关系,如果两个变量之间存在相关关系,则可以用回归方法研究一个变量对另一个变量的影响,如图所示
补充:相关分析与回归分析的联系与区别
相关分析与回归分析既有联系又有区别,其联系在于相关分析是回归分析的基础和前提,回归分析是相关分析的深入和继续。其区别主要包含以下3点。
- 相关分析所研究的两个变量是对等关系,不区分自变量和因变量,而回归分析所研究的两个变量不是对等关系,必须根据研究目的确定其中的自变量和因变量。
- 对于变量x和y来说,相关分析只能计算出一个反映两个变量间相关密切程度的相关系数,不能估计或推算出具体数值。而回归分析则可以用自变量数值推算因变量的估计值。
- 相关分析中,两个变量都是随机的,或者一个变量是随机的,另一个变量是非随机的。而回归分析中,自变量是可以控制的变量(给定的变量),因变量是随机变量。
2.线性回归的原理分析
①线性回归的一般公式
回归是研究一组随机变量与另一组变量之间关系的统计分析方法,通常用y表示因变量,而x被看成是影响y的因素,称为自变量。
线性回归就是运用直线来描述数据之间关系的一种算法。
直线的方程式可以表示为: f ( x ) = w x + b f(x)=wx+b f(x)=wx+b
w表示直线的斜率,b表示直线的截距,x表示自变量,即数据集中的特征变量, f ( x ) f(x) f(x)表示因变量,即模型对于数据结果的预测值。
在上述方程式中,只有一个x和一个 f ( x ) f(x) f(x) ,说明训练样本数据集中的特征变量只有一个,这种只有一个自变量和一个因变量组成的模型称为一元线性回归。
- 如果训练样本的数据集中有多个特征变量,则线性回归的一般预测公式为: f ( x ) = w 1 x 1 + w 2 x 2 + . . . . w n x n + b f(x)=w_1x_1+w_2x_2+....w_nx_n+b f(x)=w1x1+w2x2+....wnxn+b
x1,x2,x3…表示数据集中的特征变量(数据集中共有n个特征); f ( x ) f(x) f(x)表示模型对于数据结果的预测值;w1,w2…和b表示模型的参数,每个 w值对应一条特征直线的斜率。
像这样,由有线性关系的多个自变量和一个因变量组成的模型称为多元线性回归。线性模型的一般公式也可以这样理解,模型给出的预测值可以看作各个特征的加权和, w i w_i wi表示各个特征的权重。
②线性回归的损失函数
众所周知,平面上的两个点可以确定一条直线。假设训练数据集中只有两个样本,如表1所示。运用这两个样本很容易就可以得到一条拟合直线,如图所示。
| 序 号 | x 值 | y 值 |
|---|---|---|
| 1 | 5 | 15 |
| 2 | 15 | 35 |

如果训练数据集中增加一个样本,这个样本在坐标系中所表示的点的坐标是(10,15) 。怎样画一条直线来拟合这3个点呢?
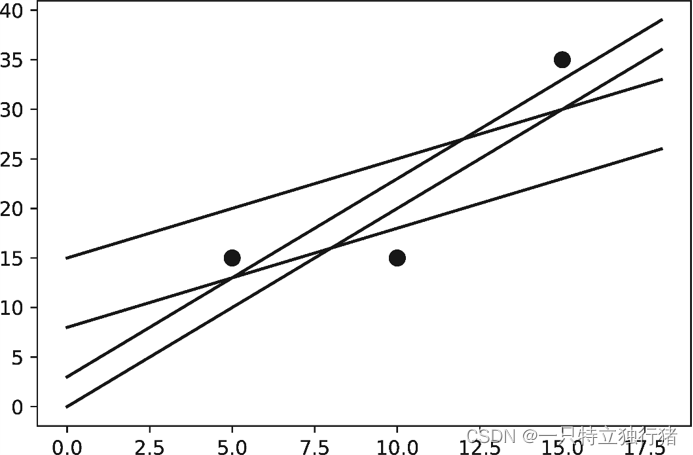
在坐标系中,先随机画出多条直线,如图。接下来通过计算来寻找最合适的拟合直线
模型输出的预测值与真实值越接近,说明模型越好。如果用 f ( x ) f(x) f(x)表示模型的预测值,y表示训练样本的真实值。那么 f ( x ) f(x) f(x)与y的接近程度就可以用“ y- f ( x ) f(x) f(x) ”来表示,实际应用中,通常用平方误差度量 f ( x ) f(x) f(x)与y的接近程度,即 e = [ f ( X ) − y ] 2 e=[f(X)-y]^2 e=[f(X)−y]2
单个样本的误差度量为 e = [ f ( X ) − y ] 2 e=[f(X)-y]^2 e=[f(X)−y]2 ,则3个样本所产生的误差总和为
J = [ y 1 − f ( x 1 ) ] 2 + [ y 2 − f ( x 2 ) ] 2 + [ y 3 − f ( x 3 ) ] 2 ] J= [y_ {1}-f(x_ {1})]^ {2} + [y_ {2}-f(x_ {2})]^ {2} + [y_ {3}-f(x_ {3})]^ {2}] J=[y1−f(x1)]2+[y2−f(x2)]2+[y3−f(x3)]2]
- 显然,只要计算出总误差J的最小值,就能找到其对应的直线,求得对应方程的参数,从而找到最合适的线性回归方程。
在机器学习的训练集中,通常有多个样本,可将上述3个样本的情况扩展到多个样本,将所有训练样本所产生的误差总和看成线性回归模型的总误差。因此,对于任意给定的n个训练样本x1…xn其标签分别为y1…yn所有样本的总误差为
J = [ y 1 − f ( x 1 ) ] 2 + [ y 2 − f ( x 2 ) ] 2 + ⋯ + [ y n − f ( x n ) ] 2 ] J= [y_ {1}-f(x_ {1})]^ {2} + [y_ {2}-f(x_ {2})]^ {2} + \cdots + [y_ {n}-f(x_ {n})]^ {2}] J=[y1−f(x1)]2+[y2−f(x2)]2+⋯+[yn−f(xn)]2]
在机器学习中,我们把上述函数J称为损失函数(loss function)。
损失函数又称错误函数或 J 函数,用来对模型的预测误差进行评估
(损失函数有很多种,这种损失函数叫做MSE均方误差)
③线性回归方程的参数求解方法
线性回归的基本思想是先求出损失函数的最小值,然后找出对应的直线,进而求出直线方程的参数w和b的值,得到线性回归方程。
求参数w和b的值有两种方法:最小二乘法和梯度下降法。
A.最小二乘法
最小二乘法又称最小平方法,它通过最小化误差的平方和寻找数据的最佳函数匹配。Sklearn的linear_model模块中提供了LinearRegression类,该类使用最小二乘法实现线性回归,可通过下面语句导入线性回归模型。
from sklearn.linear_model import LinearRegressionLinearRegression类提供了如下两个属性:
- “coef_”表示回归系数,即斜率;_
- intercept”表示截距
使用最小二乘法训练线性回归模型,预测面积为200 m2的房屋售价。二手房房屋销售数据如表所示
| 面积/(m2) | 售价/(万元) | 面积/(m2) | 售价/(万元) |
|---|---|---|---|
| 100 | 301 | 113 | 324 |
| 90 | 285 | 89 | 296 |
| 60 | 200 | 70 | 260 |
| 50 | 300 | 45 | 120 |
| 55 | 180 | 78 | 245 |
#导入NumPy与线性回归模型
import numpy as np
from sklearn.linear_model import LinearRegression
#输入训练集数据
#这里输入二维数组是为了表示两个维度,第一个维度就是样本数,第二维度是特征数
x=np.array([[100],[113],[90],[89],[60],[70],[50],[45],[55],[78]]) #房屋面积
y=np.array([[301],[324],[285],[296],[200],[260],[300],[120],[180],[245]]) #售价
#建立模型,训练模型
model=LinearRegression() #建立基于最小二乘法的线性回归模型
model.fit(x,y) #开始训练模型
#求解线性回归方程参数
print("w=",model.coef_[0],"b=",model.intercept_)
#使用逗号将不同的字符串和变量连接在一起① 在机器学习中,如果数据集比较小,一般可将其保存成数组直接写在程序中,然后让程序读取该数组的内容即可。NumPy用于创建数组对象,[1,2,3]表示一维数组,[[1,2],[3,4]]表示二维数组,本例中的数据集就是利用NumPy创建的二维数组。另外,获取数组中的数据时,下标要从0开始,本例中x[0][0]表示数据100;
② fit(x,y)表示传入数据x与标签y,训练模型。
为了便于观察,将原始数据与求得的方程用图表示出来
#导入画图工具
import matplotlib.pyplot as plt
#求模型预测值
y2=model.predict(x)
#model.predict(x)的作用是将输入数据x传递给已经训练好的模型model,然后模型会根据学习到的参数和规律,对输入数据进行预测,并返回预测结果y2
#设置坐标轴
plt.xlabel('面积') #图形横轴的标签名称
plt.ylabel('售价') #图形纵轴的标签名称
plt.rcParams['font.sans-serif']='Simhei' #中文文字设置为黑体
plt.axis([40,125,100,400]) #设置图像横轴与纵轴的最大值与最小值
#绘制并显示图形
plt.scatter(x,y,s=60,c='k',marker='o') #绘制散点图
plt.plot(x,y2,'r-') #绘制直线,第3个参数表示红色实线
plt.show() #显示图形
a=model.predict([[200]])
print("200平方米二手房的预测房价是:",a[0][0])
程序运行结果如图所示.。
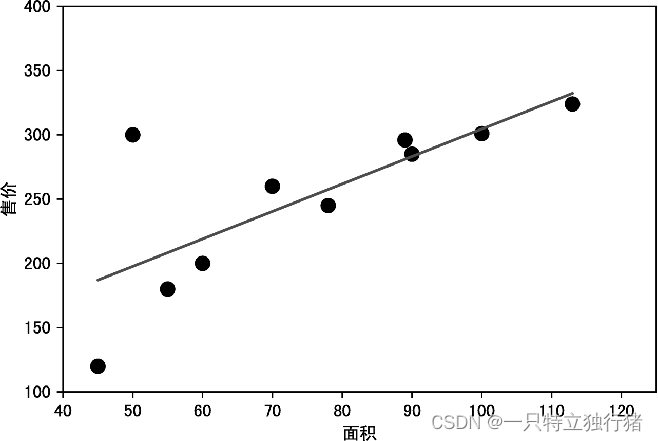
程序说明
① 得到线性回归方程后,可用predict()函数求解横坐标的预测值;
② Matplotlib中的axis([40,125,100,400])函数用于设置图像横轴和纵轴的最大值与最小值,其中,40和125分别表示横轴的最小值和最大值,100和400分别表示纵轴的最小值和最大值;
③ Matplotlib中的scatter()函数用于画散点图,前两个参数表示横轴和纵轴的坐标值,第3个参数s表示散点的大小(s值越大,点越大),c表示散点的颜色,“k”表示黑色,marker表示散点的样式,“o”表示圆点。
使用训练好的线性回归模型预测面积为200 m2的房屋售价
a=model.predict([[200]])
print("200平方米二手房的预测房价是:",a[0][0])B.梯度下降法
在机器学习中,梯度下降法是很普遍的算法,不仅可用于线性回归问题,还可用于神经网络等模型中。梯度下降法适用于特征个数较多,训练样本较多,内存无法满足要求时使用,是一种比较高效的优化方法。Sklearn中提供的SGDRegressor()函数可以实现基于梯度下降法的回归分析,该函数的语法如下。
SGDRegressor(loss=’squared_loss’,n_iter_no_change=5,max_iter=1000)
#导入NumPy与线性回归及梯度下降法模型
import numpy as np
from sklearn.linear_model import LinearRegression,SGDRegressor
#输入训练集数据
x=np.array([[100],[113],[90],[89],[60],[70],[50],[45],[55],[78]]) #房屋面积
y=np.array([[301],[324],[285],[296],[200],[260],[300],[120],[180],[245]]) #售价
#建立模型,训练模型
model=SGDRegressor(loss='huber',max_iter=5000,random_state=42)
#建立基于梯度下降法的线性回归模型
#huber代表调用huber损失函数
#5000代表迭代5000次
#random_state=42是设置随机数种子
model.fit(x,y.ravel())
#ravel()函数可以扁平化数组,即将二维数组转换为一维数组;
#开始训练模型
#求解线性回归方程参数
print("w=",model.coef_,"b=",model.intercept_)
import matplotlib.pyplot as plt
#求模型预测值
y2=model.predict(x)
#设置坐标轴
plt.xlabel('面积') #图形横轴的标签名称
plt.ylabel('售价') #图形纵轴的标签名称
plt.rcParams['font.sans-serif']='Simhei‘ #中文文字设置为黑体
plt.axis([40,125,100,400]) #设置图像横轴与纵轴的最大值与最小值
#绘制并显示图形
plt.scatter(x,y,s=60,c='k',marker='o') #绘制散点图
plt.plot(x,y2,'r-') #绘制直线,第3个参数表示红色实线
plt.legend(['真实值','预测值']) #显示图例
plt.show() #显示图形
a=model.predict([[200]])
print("200平方米二手房的预测房价是:",a[0])梯度下降法通过不断 迭代更新模型参数的方式,沿着损失函数的梯度方向逐步逼近或达到最优解。在每次迭代中,根据损失函数对参数的梯度(即损失函数对各个参数的偏导数)来更新参数,使得损失函数值逐渐减小,直到达到最小值或收敛到一个可以接受的范围内
梯度下降法的基本思想可以用以下步骤概括:
- 初始化模型参数(例如权重和偏置)的数值。
- 计算损失函数对参数的梯度。
- 根据梯度的方向和大小更新参数。
- 重复步骤2和3,直到满足停止条件(如达到最大迭代次数或损失函数变化很小)
在机器学习和深度学习中,权重(weights)和偏置(bias)是模型中的两个重要参数,用于构建模型并进行预测。
权重(weights):也就是w
- 在线性模型中,权重用于衡量输入特征对输出的影响程度。每个输入特征都与一个权重相关联,通过乘以对应的权重并求和得到模型的输出。
- 在神经网络中,权重用于连接神经元之间的信号传递。每个连接都有一个权重,控制着信号在神经网络中的传播。
- 权重决定了模型的学习能力和拟合能力,通过调整权重可以使模型更好地拟合训练数据。
偏置(bias):也就是b
- 偏置是模型中的一个常数项,用于调整模型的输出使其更符合实际情况。
- 在线性模型中,偏置相当于截距,用于调整模型在没有输入特征时的输出值。
- 在神经网络中,每个神经元都有一个偏置项,用于调整神经元的激活阈值。
在模型训练过1程中,权重和偏置是需要不断调整和优化的参数,以使模型在训练数据上达到最佳的拟合效果。通过梯度下降等优化算法,可以更新权重和偏置,使模型逐步收敛到最优解。
总的来说,权重和偏置是机器学习和深度学习模型中的关键参数,通过调整它们可以控制模型的表现。
补充
Huber损失函数定义:
[ L δ ( y , y ^ ) = { 1 2 ( y − y ^ ) 2 , for ∣ y − y ^ ∣ ≤ δ δ ( ∣ y − y ^ ∣ − 1 2 δ 2 ) , otherwise ] [ L_{\delta}(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2, & \text{for } |y - \hat{y}| \leq \delta \\ \delta(|y - \hat{y}| - \frac{1}{2}\delta^2), & \text{otherwise} \end{cases} ] [Lδ(y,y^)={21(y−y^)2,δ(∣y−y^∣−21δ2),for ∣y−y^∣≤δotherwise]
其中,( y ) 是真实值(ground truth),( y ^ \hat{y} y^ ) 是模型预测值,( δ \delta δ ) 是一个阈值参数,用于控制绝对误差和均方误差之间的平衡。当预测值与真实值之间的绝对差小于等于阈值 ( δ \delta δ ) 时,采用均方误差(MAE);否则采用绝对误差(MSE)。
为何使用Huber损失函数?
使用MAE用于训练神经网络的一个大问题就是,它的梯度始终很大,这会导致使用梯度下降训练模型时,在结束时遗漏最小值。对于MSE,梯度会随着损失值接近其最小值逐渐减少,从而使其更准确。
在这些情况下,Huber损失函数真的会非常有帮助,因为它围绕的最小值会减小梯度。而且相比MSE,它对异常值更具鲁棒性。因此,它同时具备MSE和MAE这两种损失函数的优点。不过,Huber损失函数也存在一个问题,我们可能需要训练超参数δ,而且这个过程需要不断迭代。

源码解析)

)
)



)

utils.py( 辅助函数)第一部分)

到OpenEuler虚拟机上)

如何查询特刊special issue)




