目录
一、拓扑排序
1.1、算法的基本步骤
1.2、算法实现
1.3、习题思考
1.4、DFS生成逆拓扑序
二、关键路径
1.1、关键路径的原理
1.2、算法的基本步骤
1.3、算法实现
1.4、习题思考
一、拓扑排序

➢ AOV网:在 有向图中, 顶点表示活动(或任务), 有向边表示活动(或任务)间的先后关系,称这样的有向图为AOV网(Activity On Vertex Network)。AOV网络中不能出现有向回路,即有向环。➢ 拓扑序列:就是把AOV网中的所有顶点排成一个线性序列,若AOV网中存在有向边 Vi → Vj ,则在该序列中, Vi 必位于 Vj 之前。在拓扑序列中,先进行的任务一定在后进行的任务的前面。按照拓扑序列完成各子任务,就可以顺利完成整个任务。拓扑序列未必唯一。如果不能排成一个拓扑序列,则说明AOV网络中存在有向环。
1.1、算法的基本步骤
①从图中选择一个入度为0的顶点并输出。
②从图中删除该顶点及该顶点引出的所有边。
③执行①②,直至所有顶点已输出,或剩余顶点入度均不为0(说明存在环,无法继续拓扑排序)
时间复杂度O(n+e):计算入度O(n+e),删除顶点O(n+e)。
1.2、算法实现
实际上我们并不需要真正的删除该顶点,我们只需要记录每个顶点的入度,在“删除”某个顶点之后,它所邻接到的所有顶点的入度都减1即可。并且我们用栈保存入度为0的顶点,以供删除。课本上用数组实现栈,这里直接采用STL:stack。
#include<bits/stdc++.h>
using namespace std;
#define n 10
struct Edge{int VerName;int cost;Edge * next;
};
struct Vertex{int VerName;Edge * edge=nullptr;
};
vector<int> cnt(n);
Vertex Head[n];
vector<int> path;
void TopoOrder(){//进行拓扑排序,并判断是否存在环路path.clear();cnt.assign(n,0);for(auto & i : Head){//计算入度for(Edge * edge=i.edge;edge!=nullptr;edge=edge->next){cnt[edge->VerName]+=1;//入度++}}stack<int> sta;for(int i=0;i<n;++i) if(!cnt[i]) sta.push(i);//初始化入度为0的家伙int num=0;while(!sta.empty()){//拓扑排序int cur=sta.top();sta.pop();path.emplace_back(cur);//路径存入for(Edge * edge=Head[cur].edge;edge!=nullptr;edge=edge->next){//删除点cnt[edge->VerName]-=1;//入度++if(cnt[edge->VerName]==0) sta.push(edge->VerName);}}if(path.size()!=n) printf("有向图中存在环路");else for(auto i:path) printf("%d ",i);return;
}int main(void){return 0;
}由于一个顶点的入度被删减为0时,不可能再有边指向该顶点,因此该顶点不会被再次访问,则其cnt[i]空闲了。即当cnt[i]==0时,cnt[i]就不会被访问了,i也会入栈,因此我们可以利用这个空闲直接在cnt上实现栈。
优化用cnt数组空闲空间实现栈(静态链表):
int top=-1;//模拟栈顶
for(int i=0;i<n;++i){if(cnt[i]==0){cnt[i]=top;//指向以前的栈顶top=i;//栈顶变为i}
}while(top!=-1){int cur=top;path.emplace_back(cur);top=cnt[top];//静态链表,相当于弹栈for(Edge * edge=Head[cur].edge;edge!=nullptr;edge=edge->next){//删除点cnt[edge->VerName]-=1;//入度++if(cnt[edge->VerName]==0) {cnt[edge->VerName]=top;top=edge->VerName;}}
}1.3、习题思考
(1)给定一个图和顶点序列,编写算法判断该序列是否是图的拓扑序列。
只需要先计算一次入度,然后扫描所给定的顶点序列,对于每一个顶点:
①先判断该顶点入度是否为0,如果不为0,则说明不是拓扑序,如果为0,则进行②
②将该顶点的边删除(即为其邻接顶点减少入度),之后继续扫描。
实际上我们假定给定的顶点序列是拓扑序列,则按照该顶点序列选择顶点删除边,选择的顶点一定是入度为0的。
(2)802. 找到最终的安全状态

如果本题正着想,则从一个点开始DFS遍历,如果它能遍历到终端结点,则路径上的所有点都能遍历到终端结点,如果它的所有邻接结点都是安全结点,则它也将是安全结点,如果它有一个邻接结点不是安全结点则必然它也不是安全结点(换句话说如果存在环路,则遍历到一个结点不是安全结点且已经被遍历过,则这条路并不通往终端节点,则它不是安全结点)。然后继续寻找下一个不是安全结点的结点且未被遍历过的结点开始遍历。<不是安全结点的结点且被遍历过的结点一定不可能是安全结点了,因为如果它是,那么它的所有邻接结点都是安全结点。后根DFS也将判断它为安全结点。>
如果说你能走到终端结点,你才算是安全结点。那么反过来走,只能被终端节点才能走到的结点才是安全结点。考察反向图,终端节点是入度为0的顶点,进行拓扑排序,排序过程中如果入度为0则被认为是安全结点(证明:开始时终端结点为安全结点,入度为0,删除其所有出边,剩下的结点入度为0的则说明它们只能被终端结点走到,它们是安全结点,然后把它们当作终端结点继续执行同样的操作,以此类推)。
class Solution { public:vector<int> eventualSafeNodes(vector<vector<int>>& graph) {int n=graph.size();vector<vector<int>> gra(n,vector<int>{});vector<int> cnt(n);stack<int> sta;vector<int> ans;for(int i=0;i<n;++i){cnt.at(i)=graph.at(i).size();if(!cnt.at(i)){sta.push(i);}for(int j=0;j<cnt.at(i);++j){gra.at(graph.at(i).at(j)).emplace_back(i);}}while(!sta.empty()){ans.push_back(sta.top());sta.pop();for(auto i:gra[ans.back()]){cnt.at(i)--;if(cnt.at(i)==0) sta.push(i);}}sort(ans.begin(),ans.end());return ans;} }; //什么STL大王,在这全程at(),看得脑袋晕,一般还是别用了(。。),用起来自己看不明白呀,除非你想测试越界
1.4、DFS生成逆拓扑序
为什么DFS能生成逆拓扑序?
我们来思考一下拓扑序列的原始定义。在一个拓扑序列中,如果vi在vj之前,则必然在有向图中有vi→vj。那么如果我们使用DFS“后根遍历”,则对于任意的vi→vj,一定有vi在vj之后输出,换句话说,对于有向图中的每一条边vi→vj均满足,vi在vj之后,如果将这一输出序列反转,则等价于对于有向图中的每一条边vi→vj均满足,vi在vj之前。相当于对于任何一个顶点vi,其后继邻接顶点都会在其之前被输出,否则它不会被输出。反过来就是,只有当vi被输出之后,其邻接顶点才会被输出,即满足拓扑排序。因此DFS“后根输出”为拓扑排序的逆序。
当然你得先保证这是一个AOV网络,不然DFS就变成了纯遍历了。
int vis[n]; void DFS_TopoOrder(int root){vis[root]=1;for(Edge * edge=Head[root].edge;edge!=nullptr;edge=edge->next){if(vis[root]==0)DFS_TopoOrder(edge->VerName);}printf("%d ",root);return; } for(int i=0;i<n;++i)if(cnt[i]==0) DFS_TopoOrder(i);//从入度为0的开始遍历
二、关键路径
➢AOV网(Activity On Vertex):顶点表示活动或任务(Activity), 有向边表示活动(或任务) 间的先后关系。➢AOE网(Activity On Edges):有向边表示活动或任务(Activity) , 用边上的权值表示活动的持续时间,顶点称为事件(Event): 表示其入边的任务已完成,出边的任务可开始的状态。关键路径的问题的图是只有一个源点和一个汇点的有向无环图。每一个事件,最早开始的时间取决于其前驱活动最晚完成的时间,因为只有在所有前驱活动完成了它才可以开始(这和拓扑排序很像)。完成整个工程(所有活动均被完成)所需的最短时间取决于从源点到汇点的最长路径长度,关键路径就是这条路径长度最长的路径,关键路径上的活动被称为关键活动。
1.1、关键路径的原理
(1)关键路径为什么是最长路径?
反证法证明:由于一个工程完成需要所有活动都结束。从源点出发,任意的一条道路中,走最长路径的那条路是花费时间最多的,因此工程完成至少要这条路完成。但是会不会存在一种情况使得这条路径上的某个事件被其他路径上的活动影响到,搁置了这条路的时间呢(也就是说完成整个工程的时间并不是关键路径)?我们假定存在这种情况:设这个被搁置的事件为event,该事件是关键路径上的一个事件,我们知道从源点到汇点的最长路径是 从源点经过event,再从event到汇点的。如果存在一个不是关键路径上的活动到event,关键路径上从源点到event的时间搁置了,导致完成整个工程所需的时间更长了,但是event到汇点的时间没变。由于关键路径是从源点到汇点长度最长的路径,因此关键路径应该要换成那个使得从源点到event时间更长的路径,而不是现在所说的关键路径,因此与假设的关键路径矛盾。
(2)为什么关键活动是最早开始时间和最迟开始时间相等的?
我们知道关键路径上的活动决定了整个工程完成的时间,因此如果让汇点的最早开始时间等于最迟开始时间的话,关键路径上的活动开始时间都不能推迟和提早,因此它们的最早开始时间也和最迟开始时间相同,不能被延误,如果被延误的话则汇点的开始时间也会被延误。当然我们没必要一定求出关键活动,求出“关键事件”是一样的。
(3)事件的最早开始时间应该怎么计算?
只有当一个事件的前驱事件全都完成了,它才可以开始,因此最早开始时间的计算方式是:拓扑排序指明了事件开始的必然先后顺序。
(4)事件的最迟开始时间应该怎么计算?
一个事件最迟开始的时间,就是它在不影响整个工程的时间的情况下,可以一直拖到开始的时间,因为最迟开始要让它不影响 后面事件的 最迟开始的时间,因此它是在尽可能迟的情况下尽可能不耽误,因此是取最迟里面的最小值。
1.2、算法的基本步骤
如果只需要求出从源点到汇点的最长路径的长度,只需要使用拓扑排序+动态规划就可以求出来。定义dis[i]表示从源点到顶点i的最长路径,则dis[源]=0,dis[i]=max(dis[i],dis[u]+weight(u,i));
但如果需要求出关键活动则必须求出最早发生时间和最迟发生时间相等的事件,因此需要再利用一次逆拓扑排序+动态规划求出。定义dis2[i]表示从顶点i到汇点的最长路径,则dis2[汇]=max_len,dis2[i]=min(dis2[i],dis[u]-weight(i,u))。
时间复杂度:O(n+e),拓扑排序O(n+e),动态规划O(n)
1.3、算法实现
#include<bits/stdc++.h>
using namespace std;
#define n 10
struct Edge{int VerName;int cost;Edge * next;
};
struct Vertex{int VerName;Edge * edge=nullptr;
};
vector<int> cnt(n);
Vertex Head[n];
bool TopoOrder(Vertex Head[],vector<int>& path) {path.clear();cnt.assign(n,0);for(int i=0;i<n;++i){//计算入度for(Edge * edge=Head[i].edge;edge!=nullptr;edge=edge->next){cnt[edge->VerName]+=1;//入度++}}stack<int> sta;for(int i=0;i<n;++i) if(!cnt[i]) sta.push(i);//初始化入度为0的家伙int num=0;while(!sta.empty()){//拓扑排序int cur=sta.top();sta.pop();path.emplace_back(cur);//路径存入++num;for(Edge * edge=Head[cur].edge;edge!=nullptr;edge=edge->next){//删除点cnt[edge->VerName]-=1;//入度++if(cnt[edge->VerName]==0) sta.push(edge->VerName);}}if(num!=n) {printf("有向图中存在环路");return false;}return true;;
}
vector<int > v_latest(n,0x3f3f3f3f);
vector<int > v_earliest(n);
void CriticalPath(Vertex Head[]) {vector<int> path;if(!TopoOrder(Head,path)) return;v_earliest.at(path.front())=0;for(auto i:path) {//最早开始时间for(Edge * edge=Head[i].edge;edge!=nullptr;edge=edge->next) {int k=edge->VerName;v_earliest[k]=max(v_earliest[k],v_earliest[i]+edge->cost);}}v_latest.at(path.back())=v_earliest.at(path.back());for(auto i=path.rbegin();i!=path.rend();++i) {//最迟开始时间for(Edge * edge=Head[*i].edge;edge!=nullptr;edge=edge->next) {v_latest[*i]=min(v_latest[*i],v_latest[edge->VerName]-edge->cost);}}printf("关键路径为:");for(auto i:path) {if(v_earliest[i]!=v_latest[i]) continue;for(Edge * edge=Head[i].edge;edge!=nullptr;edge=edge->next) {if(v_earliest[edge->VerName]==v_latest[edge->VerName]) {printf("%d->%d\n",i,edge->VerName);break;}}}return;
}
int main(void) {CriticalPath(Head);return 0;
}1.4、习题思考
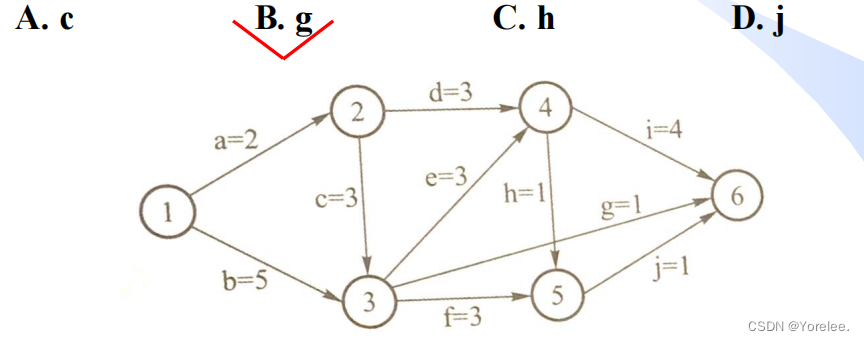
需要求活动的最早开始时间和最迟开始时间,它取决于它弧尾的最早开始时间,和弧头的最晚开始时间。










.exec不执行)



)
)

)



