专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元类型包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3.物理场问题涉及:力学、传热学、电磁学及多物理场耦合等问题的稳态(静力学)和瞬态(动力学)求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴,快速上手有限元编程,在案例中成长,摆脱按部就班填鸭式教学。
- 【所有专栏文章均提供视频教程和源码】《有限元编程从入门到精通30讲》视频教程与源码获取地址: https://www.bilibili.com/video/BV1kP4y1d7Zo
- 欢迎订阅专栏,订阅用户可私聊进入有限元编程交流群(知识交流、问题解答),并获赠丰厚的有限元相关学习资料(教材、源码、视频课)
- 专栏订阅地址:有限元编程从入门到精通_suoge223的博客-CSDN博客
文章目录
专栏导读
文章目录
【总体简介】💻🔍
【代码截图】
【理论文本截图】
【视频教程】
【总体简介】💻🔍
本程序采用的8节点厚壳单元同样是基于Mindlin/Reissner 理论的曲面壳单元,这个理论的几个基本假定是:(1)与壳的厚度相比,位移是微小的,即小位移假定;(2)垂直于中面的应力应变忽略不计,即沿厚度方向上的应力应变忽略;(3)变形前垂直于中面的直线,变形后仍保持为直线,但不一定再垂直于中面;(4)挠度和法线转角为各自独立的场函数。但是由于需要模拟面内变形,其自由度由板单元的三个自由度[u thetax thetay] 加为5个自由度[u v w phi psi ] ,前三个为平动自由度,后两个为沿着面内两个方向转动自由度,具体如图中局部坐标系中的五个自由度。由于壳结构多为空间三维结构,所以在进行有限元编程时,还会涉及局部坐标系和全局坐标系之间的转换。由于基于Mindlin/Reissner 板壳理论,所以这种壳单元还可以考虑横向剪切应力的影响,故比一般基于薄壳理论的单元准确,也因此这种单元不仅可以分析厚壳,而且可以分析薄壳,是目前为止最好的壳单元之一,哪怕现在商业有限元软件中还有六自由度的壳单元,多一个平面法线方向转动自由度,也是基于这种壳单元基础上改进的。同样要注意,在了解壳单元前,要先熟知之前课程所介绍的Kirchhoff薄板单元和mindlin厚板单元。
为了辅助理解代码背后的有限元理论,配套提供对应的理论文本,详细讲解了曲壳单元刚度矩阵的推导过程,真正消化吸收程序的内容。
你将获得:8节点壳单元matlab有限元程序源码+壳单元理论文本doc文件
获取地址:8节点空间壳单元Matlab有限元编程 | 曲壳单元 | 模态分析 | 3D壳单元 | 板壳理论| 【源代码+理论文本】
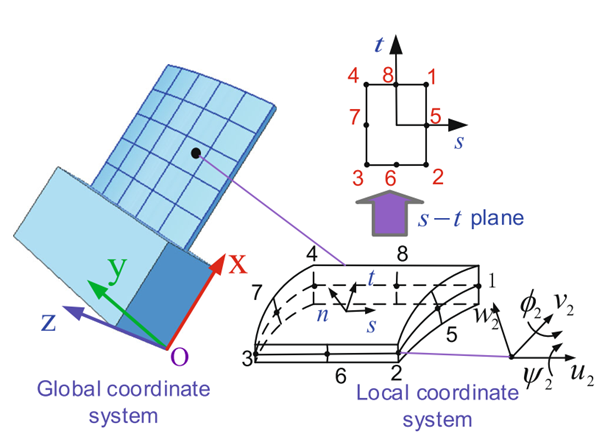
代码分析的对象为如上图所示的曲壳结构,一端固定,剩下边界自由,在端部受一集中力作用。另外还进行了该曲壳结构的模态分析,分析结果如下所示。
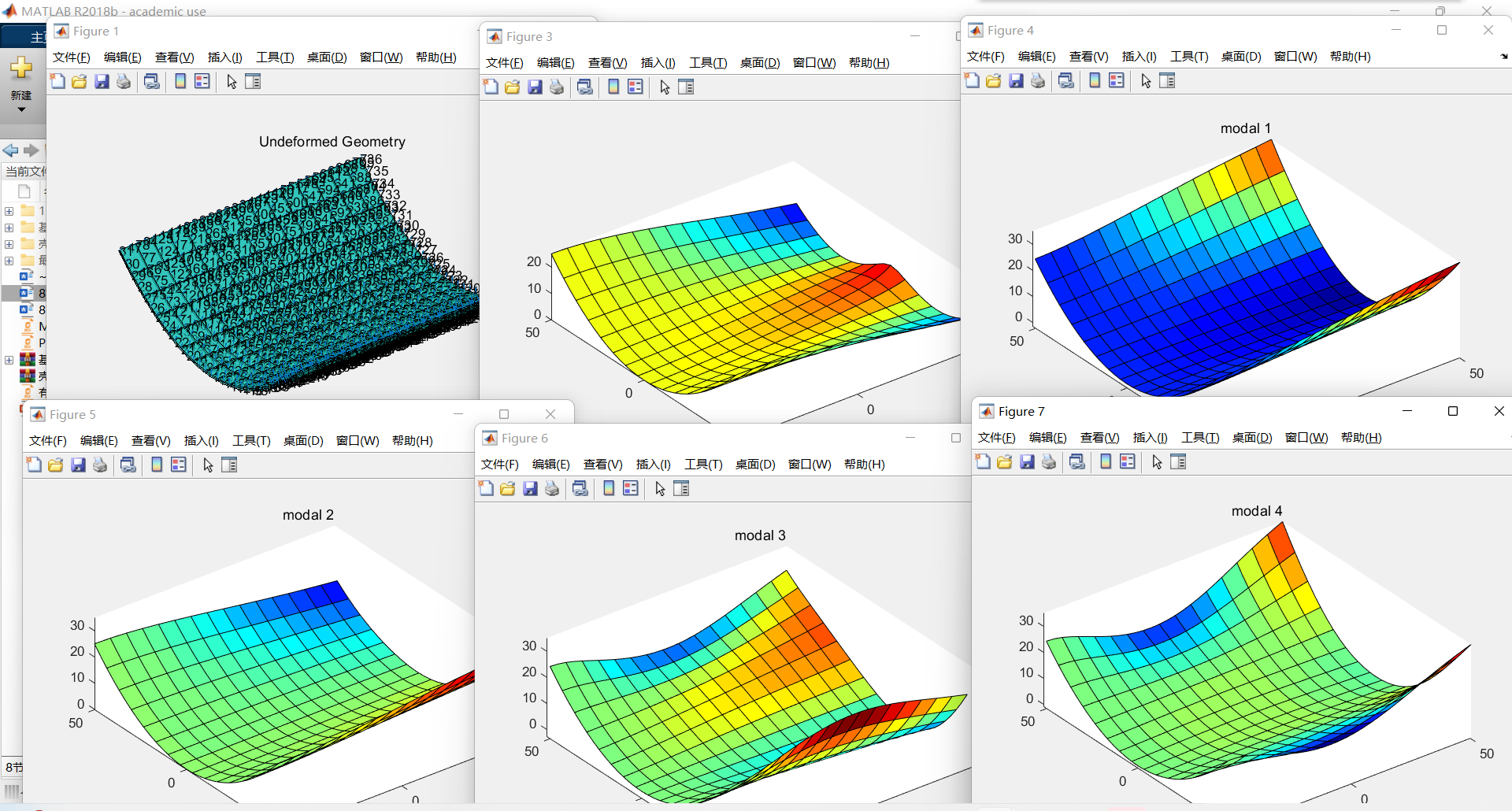
【代码截图】
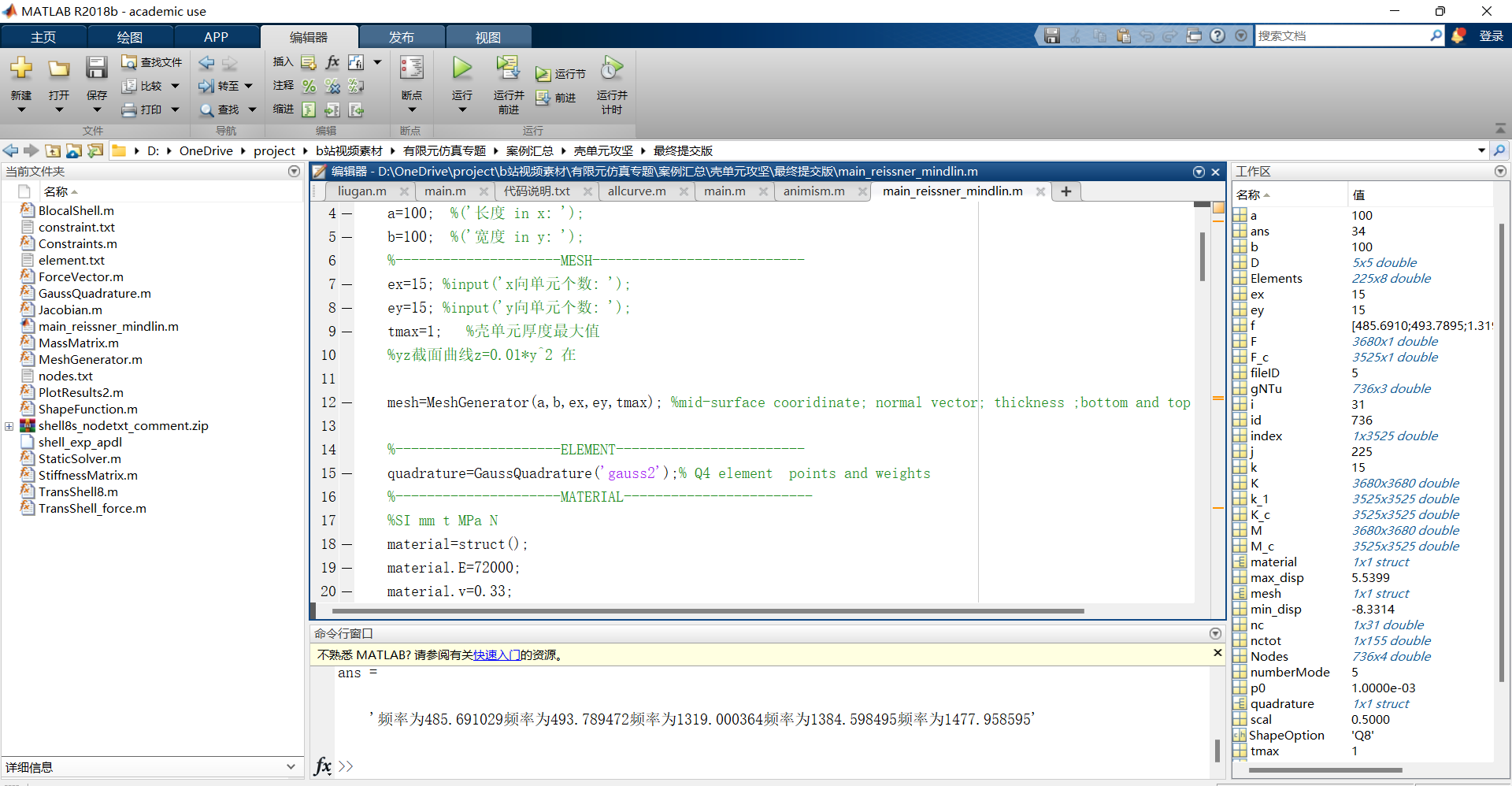
【理论文本截图】


【视频教程】
【8节点壳单元matlab有限元编程-【第1讲】课程概要/空间3D壳单元/五自由度/坐标转换/板壳力学/Reissner-Mindlin/自然坐标/局部坐标】 8节点壳单元matlab有限元编程-【第1讲】课程概要/空间3D壳单元/五自由度/坐标转换/板壳力学/Reissner-Mindlin/自然坐标/局部坐标_哔哩哔哩_bilibili



-2024年3月20日)

事件组)



![[Labtools 27-2223] Unable to connect to hw_server with URL(FPGA远程仿真器连接不上服务器问题)](http://pic.xiahunao.cn/[Labtools 27-2223] Unable to connect to hw_server with URL(FPGA远程仿真器连接不上服务器问题))



-----坐标系统与摄像机)





