更多可参考:https://github.com/Gurobi/modeling-examples/blob/master/food_manufacturing/food_manufacture_1.ipynb
一、问题简介
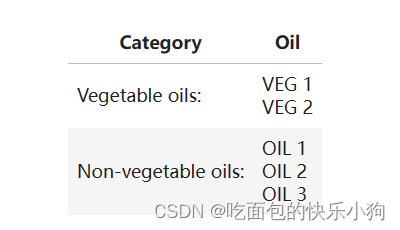
(1) 某厂商生产一种香皂的原材料有植物油脂和非植物油脂,其中植物油脂有两种,非植物油脂有三种,其中任一种都可制成香皂:
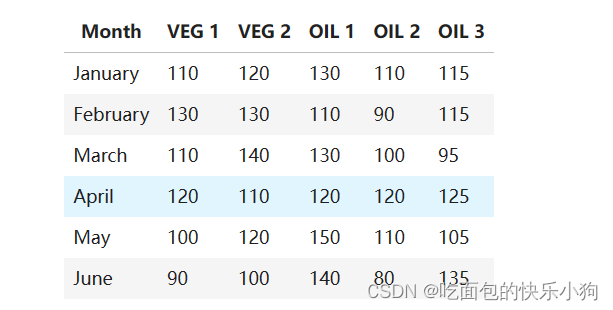
(2) 不同的时间购买原材料的价格不同:(单位: per ton)
(3)每种油脂的硬度也不同:

(4) 存储原材料会产生存储费用,5 per month per 1000 ton
(5) 一月份的时候每种油脂都存储了500 ton, 要求6月份结束的时候依然剩下相同的原材料
(6) 最终的香皂售价为150 per ton
(7) 该厂商每个月最多可以加工200 ton植物油脂和250 ton 非植物油脂;
(8) 加工过程中没有浪费,被加工的油脂的重量与最终的香皂的重量相同;
(9) 最终的香皂的硬度必须在3到6之间,香皂的硬度由油脂线性混合;
问:每个月应该买多少原材料和生产多少肥皂才能最大化这六个月的总利润?
二、建模
1、集合
t ∈ M o n t h s = { J a n , F e b , M a r , A p r , M a y , J u n } t \in Months= \set{ Jan, Feb,Mar,Apr,May,Jun } t∈Months={Jan,Feb,Mar,Apr,May,Jun}
V = { V E G 1 , V E G 2 } V = \set{ VEG1, VEG2 } V={VEG1,VEG2}
N = { N V E G 1 , N V E G 2 , N V E G 3 } N = \set{ NVEG1, NVEG2, NVEG3 } N={NVEG1,NVEG2,NVEG3}
o ∈ O i l s = { V E G 1 , V E G 2 , N V E G 1 , N V E G 2 , N V E G 3 } o \in Oils = \set{VEG1, VEG2, NVEG1, NVEG2,NVEG3} o∈Oils={VEG1,VEG2,NVEG1,NVEG2,NVEG3}
2、参数
price: 每吨香皂的售价
init_store: 一月份开始的原料存储量
target_store: 六月份剩余的原料存储量
store_cost : 每个月每1000吨原料的存储费用
veg_cap: 厂商每个月可以加工的植物油脂的量
nveg_cap:厂商每个月可以加工的非植物油脂的量
min_hardness:香皂要求的最小硬度
max_hardness:香皂要求的最大硬度
hardness(o): 每种油脂o的硬度
cost(o, t):每种油脂每个月的购买价格
3、决策变量
p r o d u c e t produce_{t} producet: 每个月生产肥皂的量
b u y o , t buy_{o,t} buyo,t:每个月购买油脂的量
c o n s u m o , t consum_{o,t} consumo,t:每个月消耗的油脂的量
s t o r e o , t store_{o,t} storeo,t:每个月存储的油脂的量
4、目标函数
最大化这六个月的净利润:
m a x z = ∑ t ∈ M o n p r i c e ∗ p r o d u c e t − ∑ t ∈ M o n ∑ o ∈ O i l s ( c o n s u m o , t ∗ c o s t o , t + s t o r e _ c o s t ∗ s t o r e o , t ) max z = \sum_{t\in Mon}price*produce_{t}-\sum_{t\in Mon} \sum_{o\in Oils} (consum_{o,t}*cost_{o,t}+store\_cost*store_{o,t}) maxz=∑t∈Monprice∗producet−∑t∈Mon∑o∈Oils(consumo,t∗costo,t+store_cost∗storeo,t)
5、约束条件
(1)1月份的物质守恒约束:
i n i t _ s t o r e + b u y o , J a n = c u n s u m o , t + s t o r e o , t , o ∈ O i l s init\_store + buy_{o,Jan} = cunsum_{o,t}+store_{o,t}, o\in Oils init_store+buyo,Jan=cunsumo,t+storeo,t,o∈Oils
(2) 2-6月份的物质守恒约束:
s t o r e o , t − 1 + b u y o , t = c u n s u m o , t + s t o r e o , t , o ∈ O i l s store_{o,t-1} + buy_{o,t} = cunsum_{o,t}+store_{o,t}, o\in Oils storeo,t−1+buyo,t=cunsumo,t+storeo,t,o∈Oils
(3) 6月份的剩余油脂约束:
s t o r e o , J u n = t a r g e t _ s t o r e , o ∈ O i l s store_{o,Jun} = target\_store, o\in Oils storeo,Jun=target_store,o∈Oils
(4)油脂加工能力约束:
∑ o ∈ V c o n s u m o , t < = v e g _ c a p , t ∈ M o n \sum_{o \in V} consum_{o,t} <= veg\_cap, t\in Mon ∑o∈Vconsumo,t<=veg_cap,t∈Mon
∑ o ∈ N c o n s u m o , t < = n v e g _ c a p , t ∈ M o n \sum_{o \in N} consum_{o,t} <= nveg\_cap, t\in Mon ∑o∈Nconsumo,t<=nveg_cap,t∈Mon
(5)香皂硬度约束:
m i n _ h a r d n e s s ∗ p r o d u c t t < = ∑ o ∈ O i l s h a r d n e s s o ∗ c o n s u m o , t < = m a x h a r d n e s s ∗ p r o d u c t t min\_hardness*product_{t} <= \sum_{o\in Oils}hardness_{o}*consum_{o,t} <= max_hardness*product_{t} min_hardness∗productt<=∑o∈Oilshardnesso∗consumo,t<=maxhardness∗productt
(6)质量守恒约束:
∑ o ∈ O i l s c o n s u m o , t = p r o d u c e t , t ∈ M o n \sum_{o\in Oils}consum_{o,t}=produce_{t}, t\in Mon ∑o∈Oilsconsumo,t=producet,t∈Mon
三、代码实现
import gurobipy as gb
from gurobipy import *# set
mon = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun'] # 有序的
veg = ['V1', 'V2']
nveg = ['N1','N2','N3']hardness = dict({'V1': 8.8,'V2': 6.1,'N1': 2.0,'N2': 4.2,'N3': 5.0
})init_store = dict({'V1': 500,'V2': 500,'N1': 500,'N2': 500,'N3': 500
})arcs, cost = gb.multidict({('Jan','V1'):110, ('Jan','V2'):120,('Jan','N1'):130,('Jan','N2'):110,('Jan','N3'):115,('Feb','V1'):130, ('Feb','V2'):130, ('Feb','N1'):110, ('Feb','N2'):90, ('Feb','N3'):115,('Mar','V1'):110, ('Mar','V2'):140, ('Mar','N1'):130, ('Mar','N2'):100, ('Mar','N3'):95,('Apr','V1'):120, ('Apr','V2'):110, ('Apr','N1'):120, ('Apr','N2'):120, ('Apr','N3'):125,('May','V1'):100, ('May','V2'):120, ('May','N1'):150, ('May','N2'):110, ('May','N3'):105,('Jun','V1'):90, ('Jun','V2'):100, ('Jun','N1'):140, ('Jun','N2'):80, ('Jun','N3'):135
})
# parameters
price = 150 # 单位香皂的售价
veg_cap = 200 # 植物油脂的加工能力上限
nveg_cap = 250 # 非植物油脂的加工能力上限
min_hardness = 3 # 硬度的下限
max_hardness = 6
store_cost = 5 # 单位原料存储费用# model
model = gb.Model()
# decision var(各决策变量之间是满足某种关系的)
produce = model.addVars(mon, name = 'produce')
buy = model.addVars(arcs, name = 'buy')
consum = model.addVars(arcs, name = 'consum')
store = model.addVars(arcs, name = 'store')# constraints
oils = hardness.keys()
# 1月份的物质守恒约束
model.addConstrs((init_store[o] + buy['Jan', o] == consum['Jan', o] + store['Jan',o] for o in oils), name = 'Jan constraints')
# 2-6月份的物质守恒约束
model.addConstrs((store[mon[t-1],o] + buy[mon[t], o] == consum[mon[t], o] + store[mon[t],o] for t in range(1,len(mon)) for o in oils), name = 'other mon constraints' )
# 6月份的剩余油脂约束
model.addConstrs((store['Jun', o] == init_store[o] for o in oils), name = 'Jun constraints')
# 油脂加工能力约束
model.addConstrs((gb.quicksum(consum[t, v] for v in veg) <= veg_cap for t in mon), name = 'veg constraints')
model.addConstrs((gb.quicksum(consum[t, nv] for nv in nveg) <= nveg_cap for t in mon), name = 'nveg constraints')
# 香皂硬度约束
model.addConstrs((min_hardness*produce[t] <= gb.quicksum(hardness[o]*consum[t,o] for o in oils) for t in mon), name = 'min hardness constraints')
model.addConstrs((max_hardness*produce[t] >= gb.quicksum(hardness[o]*consum[t,o] for o in oils) for t in mon), name = 'min hardness constraints')
# 总的质量守恒约束
model.addConstrs((produce.sum(t,'*') == consum.sum(t, '*') for t in mon), name = 'per month total mass constraints')# objective
obj = price*produce.sum() - (buy.prod(cost) + store_cost*store.sum())
model.setObjective(obj, GRB.MAXIMIZE)# optimize
model.optimize()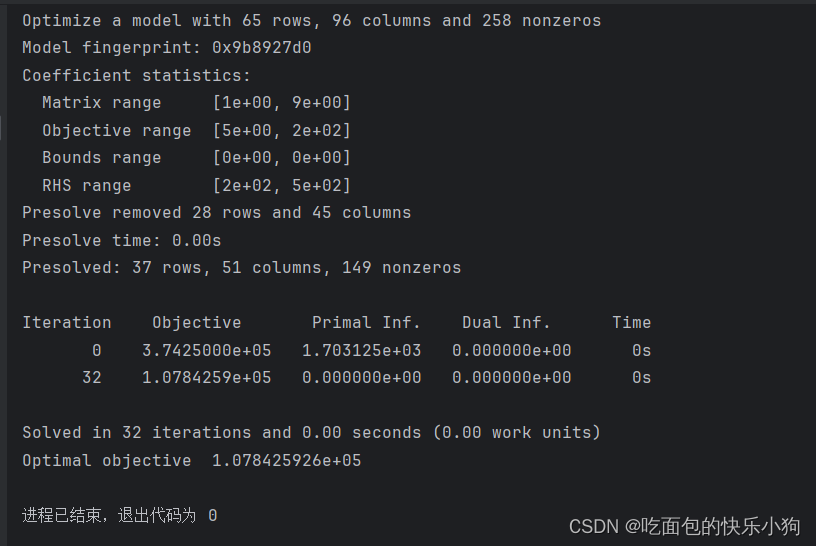
 SpringMVC框架的简单创建与使用,快速上手)
)



)




)


Linux和Docker)





