推荐系统中常用评价指标及其实现
定义
0 符号系统
| 符号 | 含义 | 备注 |
|---|---|---|
| K, k | Top-K 推荐中的 K 值, 比如 Top-5 表示给每个用户推荐 5 个物品 | |
| U U U | 用户总数量 | |
| I I I | 物品总数量 | |
| u u u | 代指一个用户 | |
| i i i | 代指一个物品 | |
| R ( u ) \mathcal{R}(u) R(u) | 给用户 u u u 推荐的物品列表 | |
| T ( u ) \mathcal{T}(u) T(u) | 用户 u u u 的真实交互列表 |
1 评分指标
1.1 平均绝对误差(Mean Absolute Error, MAE)
1.2 均方误差(Mean Squared Error)
1.2 均方根误差(Root Mean Absolute Error, RMSE)
2 准确性指标
2.1 召回率(Recall)
Recall 表示推荐的列表中预测正确的占总体的比例.
R e c a l l @ K = 1 U ∑ u = 1 U ∣ R ( u ) ∩ T ( u ) ∣ ∣ T ( u ) ∣ \mathrm{Recall}@K=\frac{1}{U}\sum_{u=1}^{U}\frac{\mid\mathcal{R}(u)\cap\mathcal{T}(u)\mid}{\mid\mathcal{T}(u)\mid} Recall@K=U1u=1∑U∣T(u)∣∣R(u)∩T(u)∣
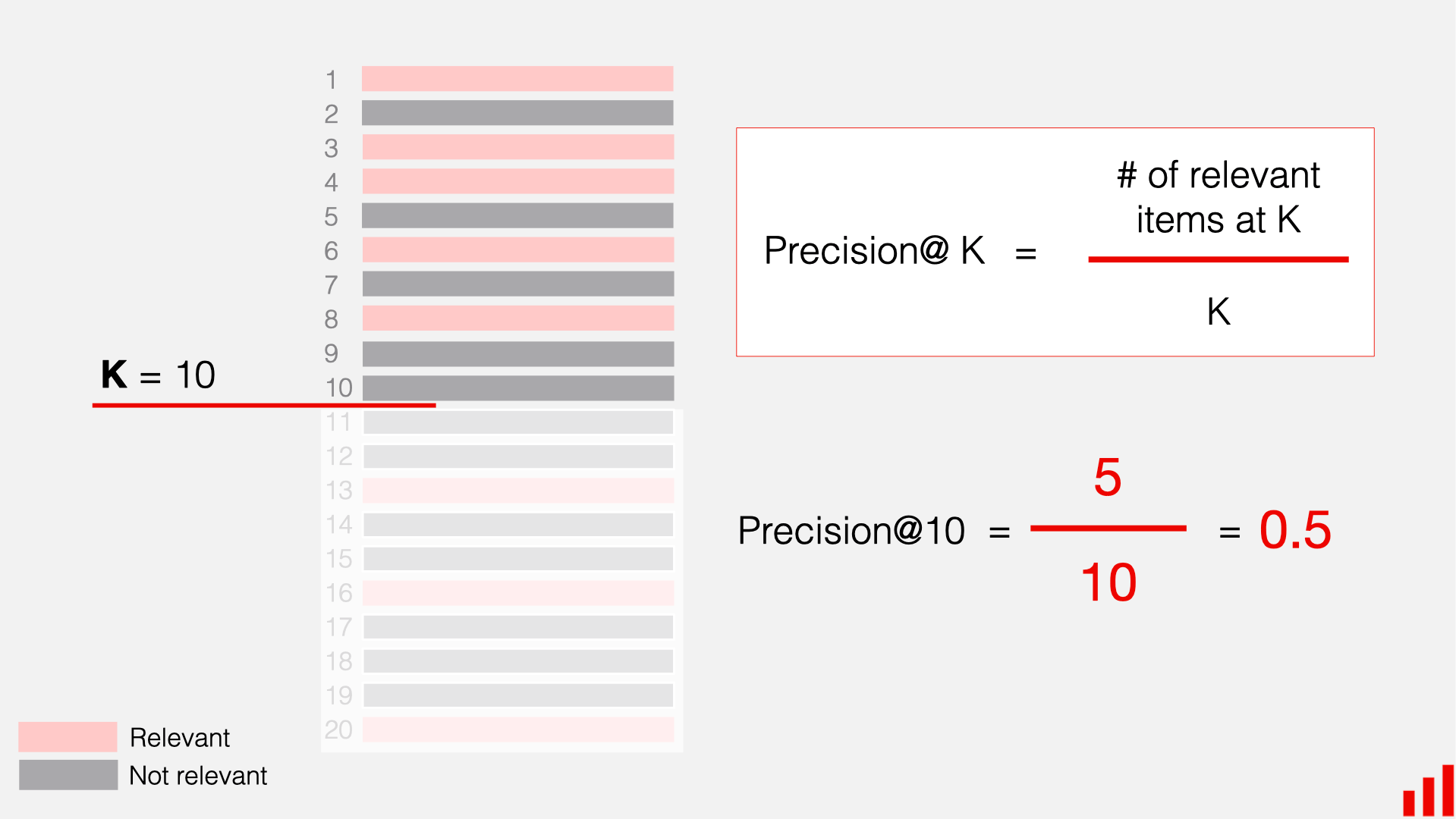
2.2 精确度(Precision)
Precision 表示推荐的列表中有多少是正确的.
P r e c i s i o n @ K = 1 U ∑ u = 1 U ∣ R ( u ) ∩ T ( u ) ∣ ∣ R ( u ) ∣ = 1 U ∑ u = 1 U ∣ R ( u ) ∩ T ( u ) ∣ K \mathrm{Precision}@K=\frac{1}{U}\sum_{u=1}^{U}\frac{\mid\mathcal{R}(u)\cap\mathcal{T}(u)\mid}{\mid\mathcal{R}(u)\mid}=\frac{1}{U}\sum_{u=1}^{U}\frac{\mid\mathcal{R}(u)\cap\mathcal{T}(u)\mid}{K} Precision@K=U1u=1∑U∣R(u)∣∣R(u)∩T(u)∣=U1u=1∑UK∣R(u)∩T(u)∣
3 排名指标
3.1 命中率(Hit Ratio, HR)
HR 表示推荐列表中至少有一个物品命中的比例.
H R @ K = 1 U ∑ u = 1 U h r ( u ) h r ( u ) = { 1 , R ( u ) ∩ T ( u ) ≠ ∅ 0 , R ( u ) ∩ T ( u ) = ∅ \mathrm{HR}@K=\frac{1}{U}\sum_{u=1}^{U}\mathrm{hr}(u)\\ \mathrm{hr}(u)=\left\{ \begin{aligned} &1,\mathcal{R}(u)\cap\mathcal{T}(u)\neq\varnothing\\ &0,\mathcal{R}(u)\cap\mathcal{T}(u)=\varnothing \end{aligned} \right. HR@K=U1u=1∑Uhr(u)hr(u)={1,R(u)∩T(u)=∅0,R(u)∩T(u)=∅
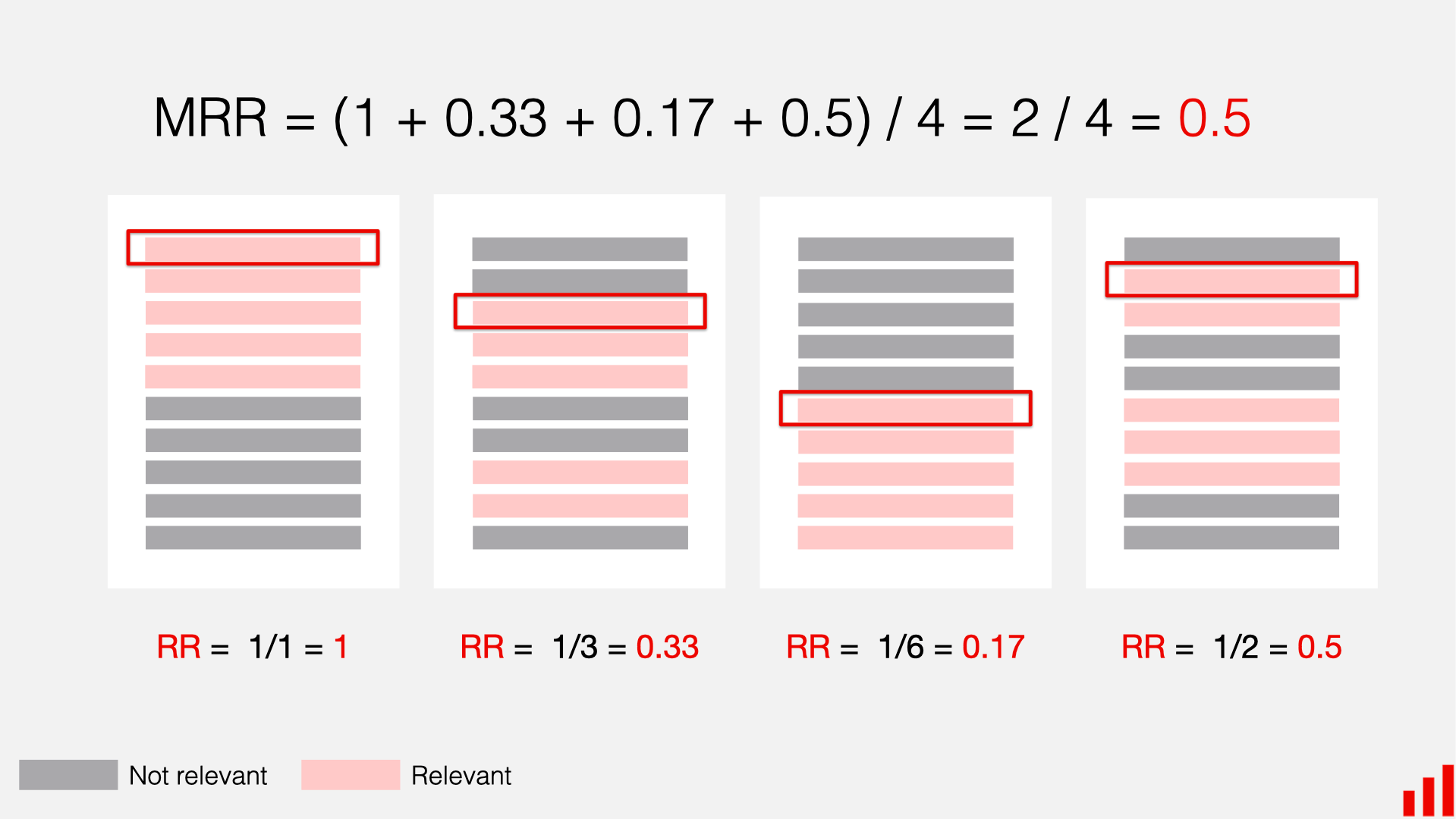
3.2 平均倒数排名(Mean Reciprocal Rank, MRR)
M R R @ K = 1 U ∑ u = 1 U 1 r a n k ( u ) \mathrm{MRR}@K=\frac{1}{U}\sum_{u=1}^{U}\frac{1}{\mathrm{rank}(u)} MRR@K=U1u=1∑Urank(u)1
r a n k ( u ) \mathrm{rank}(u) rank(u)表示对用户 u u u 的推荐中( R ( u ) \mathcal{R}(u) R(u)), 第一个命中的项目在推荐列表( R ( u ) \mathcal{R}(u) R(u))中的次序, 若没有命中, 则 r a n k ( u ) → ∞ \mathrm{rank}(u)\to\infty rank(u)→∞.
3.3 Mean Average Precision (MAP)
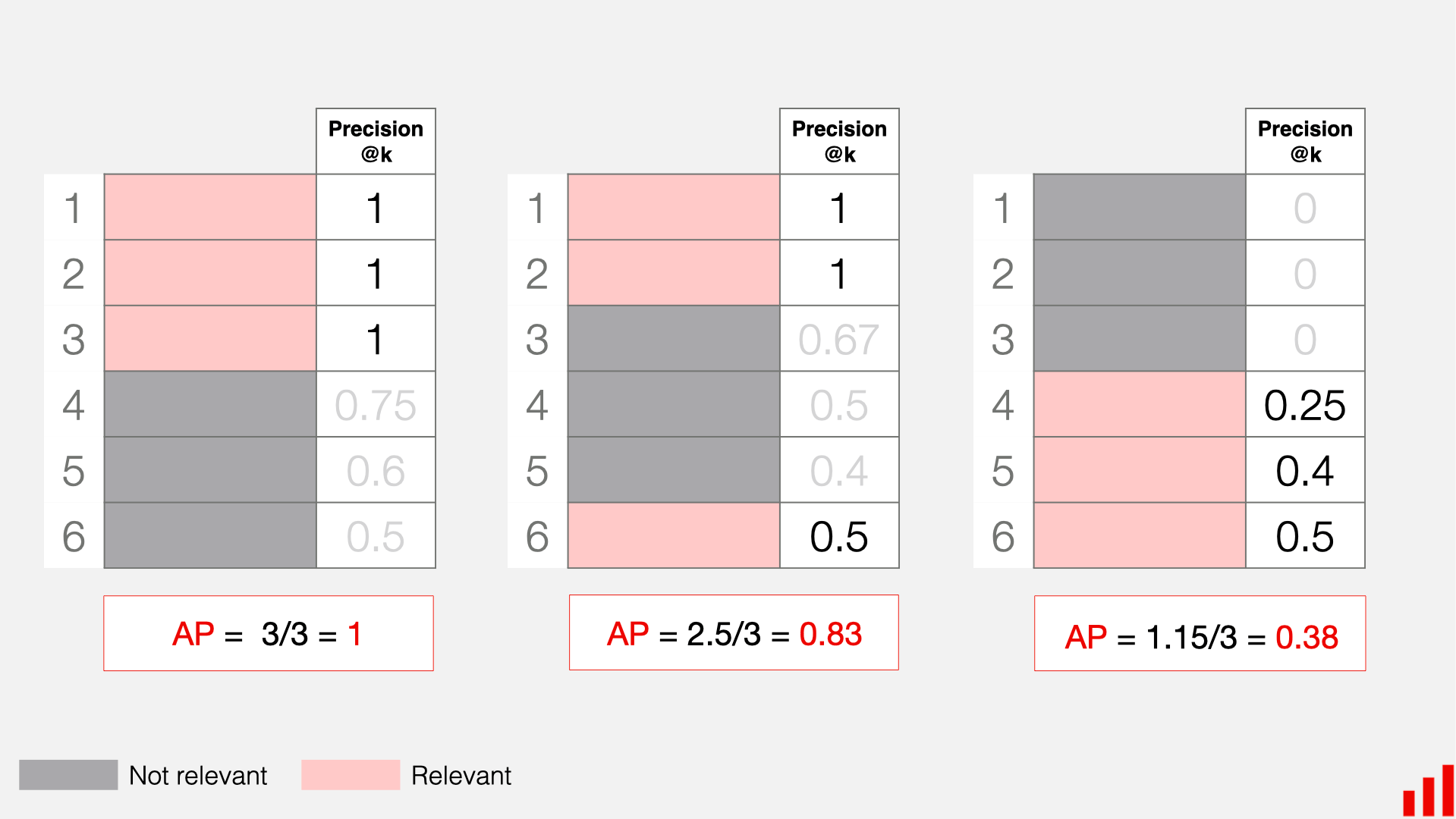
M A P @ K = 1 U ∑ u = 1 U A P @ K u A P @ K u = 1 ∣ R ( u ) ∩ T ( u ) ∣ ∑ k = 1 K P r e c i s i o n ( k ) × r e l ( k ) \mathrm{MAP}@K=\frac{1}{U}\sum_{u=1}^{U}{\mathrm{AP}@K}_{u}\\ {\mathrm{AP}@K}_{u}=\frac{1}{\mid\mathcal{R}(u)\cap\mathcal{T}(u)\mid}\sum_{k=1}^{K}\mathrm{Precision}(k)\times\mathrm{rel}(k) MAP@K=U1u=1∑UAP@KuAP@Ku=∣R(u)∩T(u)∣1k=1∑KPrecision(k)×rel(k)
P r e c i s i o n ( k ) \mathrm{Precision}(k) Precision(k): 计算用户 u u u 的推荐列表中的第 k k k 个元素位置的 P r e c i s i o n @ k \mathrm{Precision}@k Precision@k.
r e l ( k ) \mathrm{rel}(k) rel(k): 当用户 u u u 的推荐列表中的第 k k k 个元素命中时 r e l ( k ) = 1 rel(k)=1 rel(k)=1, 否则 r e l ( k ) = 0 rel(k)=0 rel(k)=0.

3.4 归一化折损累计增益(Normalized Discounted Cumulative Gain, NDCG)
N D C G @ K = 1 U ∑ u = 1 U D C G @ K u I D C G @ K D C G @ K u = ∑ i = 1 K r e l ( i ) log 2 ( i + 1 ) I D C G @ K = ∑ i = 1 K 1 log 2 ( i + 1 ) \mathrm{NDCG}@K=\frac{1}{U}\sum_{u=1}^{U}\frac{\mathrm{DCG}@K_{u}}{\mathrm{IDCG}@K}\\ \mathrm{DCG}@K_{u}=\sum_{i=1}^{K}\frac{\mathrm{rel}(i)}{\log_{2}(i+1)}\\ \mathrm{IDCG}@K=\sum_{i=1}^{K}\frac{1}{\log_{2}(i+1)} NDCG@K=U1u=1∑UIDCG@KDCG@KuDCG@Ku=i=1∑Klog2(i+1)rel(i)IDCG@K=i=1∑Klog2(i+1)1
r e l ( i ) \mathrm{rel}(i) rel(i): 当用户 u u u 的推荐列表中的第 i i i 个元素命中时 r e l ( i ) = 1 rel(i)=1 rel(i)=1, 否则 r e l ( i ) = 0 rel(i)=0 rel(i)=0.
3.5 多样性
3.6 新颖性
新颖性评估推荐物品对用户的独特程度, 它衡量推荐物品与流行物品的不同程度.
3.7 惊喜度
3.8 信任度
3.9 实时性
3.10 健壮性
实现
参考资料
[1] 推荐系统有哪些常用的评价标准
[2] 推荐系统研究中常用的评价指标
[3] 【推荐算法】从零开始做推荐(二)——TopK推荐的评价指标,计算原理与样例
[4] 推荐系统常用评价指标及其 Python 实现
[5] 推荐系统中的常用评价指标:NDCG,Recall,AUC,GAUC
[6] 评价指标 - HR, MRR, NDCG
[7] 详解评价指标MAP和NDCG(从推荐系统的角度)
[8] 如何理解推荐系统中的MAP评估指标?
[9] 10 metrics to evaluate recommender and ranking systems
[10] Mean Average Precision (MAP) in ranking and recommendations
[11] Normalized Discounted Cumulative Gain (NDCG) explained
[12] Mean Reciprocal Rank (MRR) explained



















)