1、引入:单变量数据拟合
原先的插值要求给出的数据点要在拟合的函数上,但数据拟合,只需整体“近似”,不强求所有的数据点一致
假设给出数据:
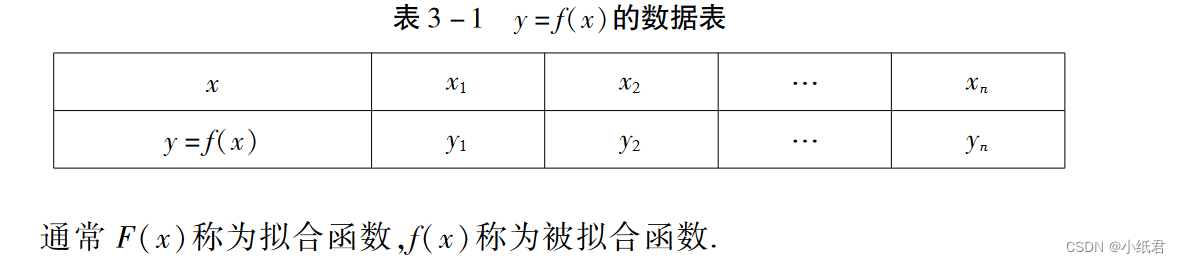
那么 偏差 的定义为:
但是偏差“大小”,最好是用绝对值表示,因此,运算时将拟合函数和被拟合函数之间的偏差表示为:
对于单变量数据:上述是一个标量

设拟合函数为:
那么偏差值 =
要使偏差值最小,求解目标是a和b,则用偏差值(函数)对a和b求偏导
设偏差值函数为
令偏导等于0,那么就能得到两个方程,足以解两个未知数
2、多变量数据拟合
基本的求解思路:求偏差函数——求偏导——解方程 已经通过上述内容展示过了,对于多变量数据我们考虑的情况是:
当 不是一个标量而是一个向量,也就是说对于被拟合的原函数,它有若干个自变量
可以设拟合函数为 【注意:这里的
不是一个一个的数据点,而是一个数据x向量的x1坐标,x2坐标,...,xn坐标】
给定数据表格:
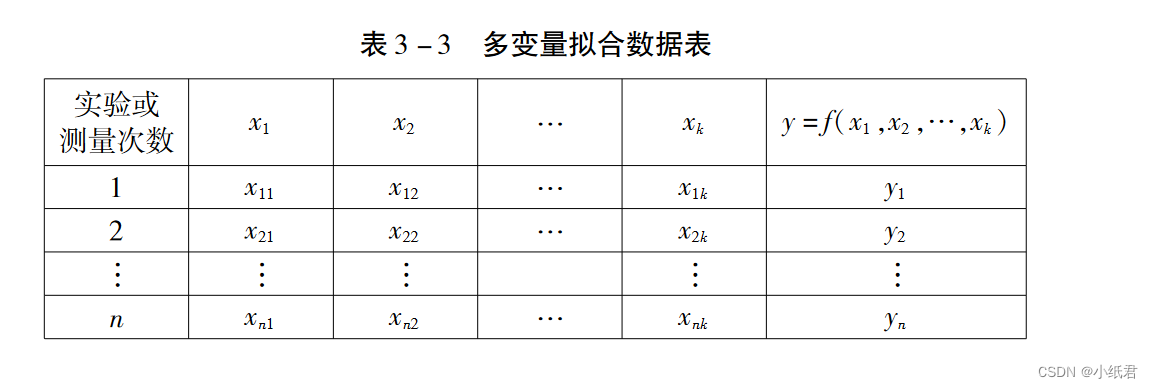 我们假设表中数据呈线性关系[这里指的是y和x],则可以设
我们假设表中数据呈线性关系[这里指的是y和x],则可以设
依旧求偏差:
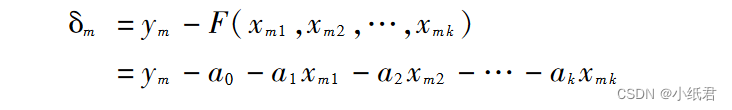
然后求偏导,具体偏导求解不再展开,因为下文要介绍更为简单、便于【计算机】计算的矩阵形式
2、矩阵形式
1)知识准备
参考:矩阵的四大基础子空间 - 知乎 (zhihu.com)
a) 矩阵四个基本子空间
对于一个矩阵A:
列空间(C(A)): 假设存在x,使得Ax = b,那么b属于A的列空间
零空间 :所有满足的向量
的集合就称之为矩阵A的零空间
行空间(R(A)):假设存在x,使得 ,那么b属于R(A)
左零空间 :所有满足的向量y的集合,称为矩阵A的左零空间,记为
b) 四空间的正交关系
正交的定义:两个向量的点积为零,那么这两个向量是正交的
空间正交的定义:如果两个空间中的任意的两个向量是正交的,则这两个空间的正交的
四空间的正交关系:
- 列空间与左零空间正交
- 行空间与零空间正交
2)数据拟合的矩阵形式
对
可以改写为矩阵:
原函数为 :
代入真实的数据点(以表3-2的数据为例子),那么各个矩阵结果为:
对于Ax = b
若有解,那么偏差应该是0,所有的数据点都被拟合到了
若无解,那么要考虑使得偏差最小的向量x
偏差的表达式 =
使得偏差的模长最小,即,求导:
则要使偏差模长最小,就要令
2)编程测一下
例题:
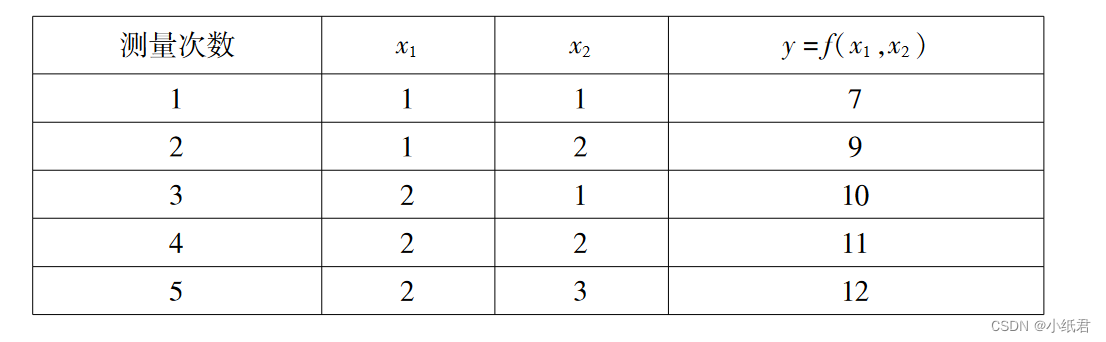
import numpy as npdef createA_b(X,Y):n = len(X)dim = len(X[0])+1A = np.ones(shape=(n,dim))b = np.zeros(shape=(n,1))for row in range(n):b[row][0] = Y[row]for i in range(1,dim):A[row][i] = X[row][i-1]return A,b# A^Ttmp = 0 算tmp
def cal_Right(A):s = A.shape[0]Zero = np.zeros(shape=(s,1))x,_,_,_ = np.linalg.lstsq(A,Zero,rcond=None)return xX = [[1,1],[1,2],[2,1],[2,2],[2,3]]
Y = [7,9,10,11,12]
A,b = createA_b(X,Y)# 使用最小二乘法求解 Ax = b(不要求方阵)
Ax_b = cal_Right(A.T)
x,residuals,_,_ = np.linalg.lstsq(A,b+Ax_b,rcond=None)print("解向量 x:\n", x)
print("残差平方和:", residuals)结果:

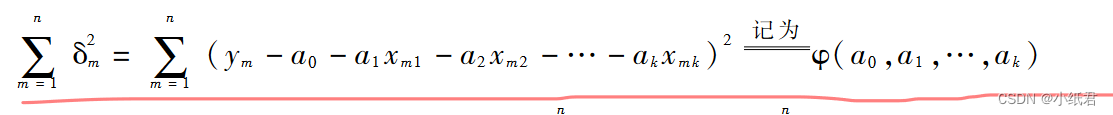

类的6个默认成员函数及const成员函数)



)
)
![[Halcon学习笔记]标定常用的Halcon标定板规格及说明](http://pic.xiahunao.cn/[Halcon学习笔记]标定常用的Halcon标定板规格及说明)











)