B 题 多波束测线问题
单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀速直线传播,在不同界面上产生反射,利用这一原理,从测量船换能器垂直向海底发射声波信号,并记录从声波发射到信号接收的传播时间,通过声波在海水中的传播速度和传播时间计算出海水的深度,其工作原理如图 1 所示。由于单波束测深过程中采取单点连续的测量方法,因此,其测深数据分布的特点是,沿航迹的数据十分密集,而在测线间没有数据。
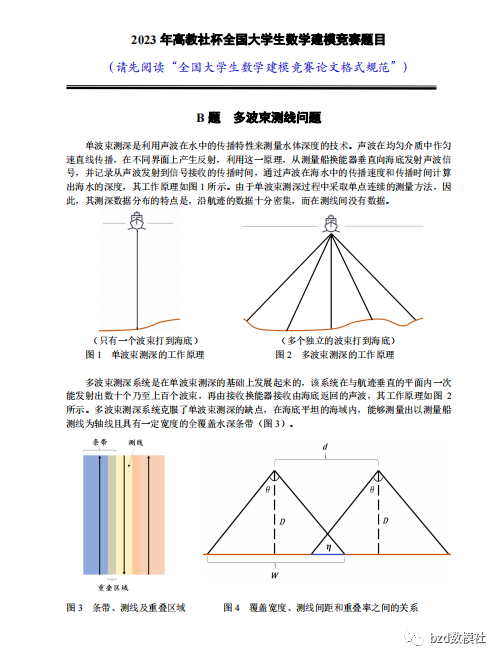
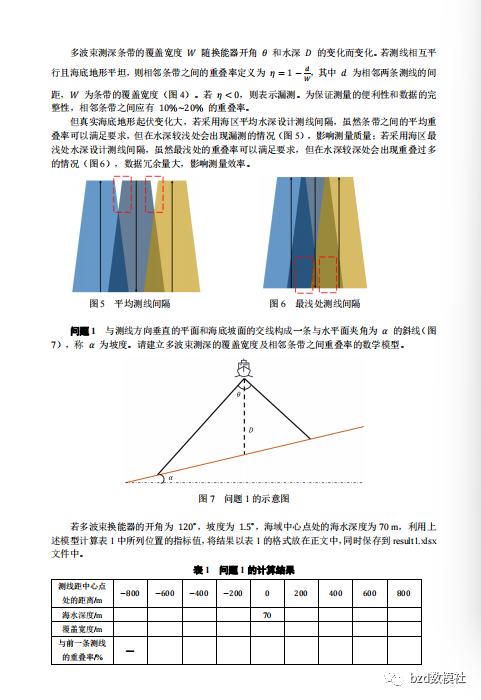
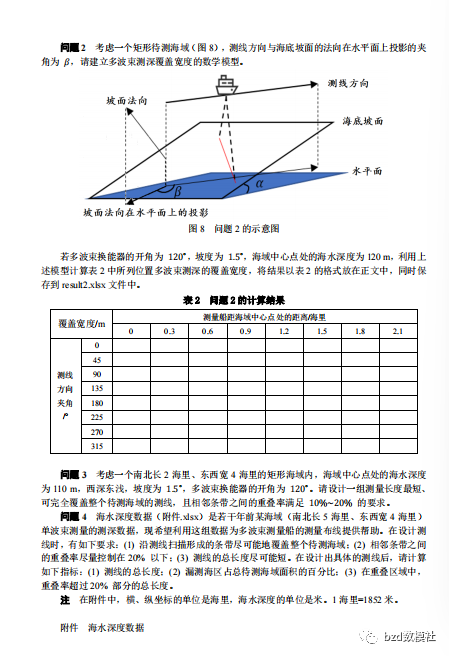
单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀速直线传播,在不同界面上产生反射,利用这一原理,从测量船换能器垂直向海底发射声波信号,并记录从声波发射到信号接收的传播时间,通过声波在海水中的传播速度和传播时间计算出海水的深度,其工作原理如图 1 所示。由于单波束测深过程中采取单点连续的测量方法,因此,其测深数据分布的特点是,沿航迹的数据十分密集,而在测线间没有数据。



本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/75505.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!