递归：通过自我调用解决问题的函数

注意：

#1.递归出口

#2.当前问题如何变成子问题

例子：利用递归写一个阶乘函数，F(n),求n的阶乘

def f(n):if n <= 1:return 1ans = n * f(n-1)return ans
print(f(5))

---

---

---

例子：汉诺塔问题

Hanoi塔由n个大小不同的圆盘和三根木柱a,b,c组成。开始时，这n个圆盘由大到小依次套在a柱上，如图所示。要求把a柱上n个圆盘按下述规则移到c柱
(1)一次只能移一个圆盘;
(2)圆盘只能在三个柱上存放;
(3)在移动过程中，不允许大盘压小盘。
问将这n个盘子从a柱移动到c柱上，输出如何移动?

---

思路：

定义函数 Move，表示n个盘子，从A挪到C，中间通过B来挪动Move(n，A，B，C)
考虑n个盘子的时候，将上面n-1个盘子看做一个整体
1、首先需要将n-1个盘子从A挪到B，通过c，这就变成递归的问题Move(n-1，A，C，B);
2、然后移动:A->C
3、最后将n-1个盘子从B挪到C，通过A，Move(n-1，B，A，C);
4、n=0的时候，递归出口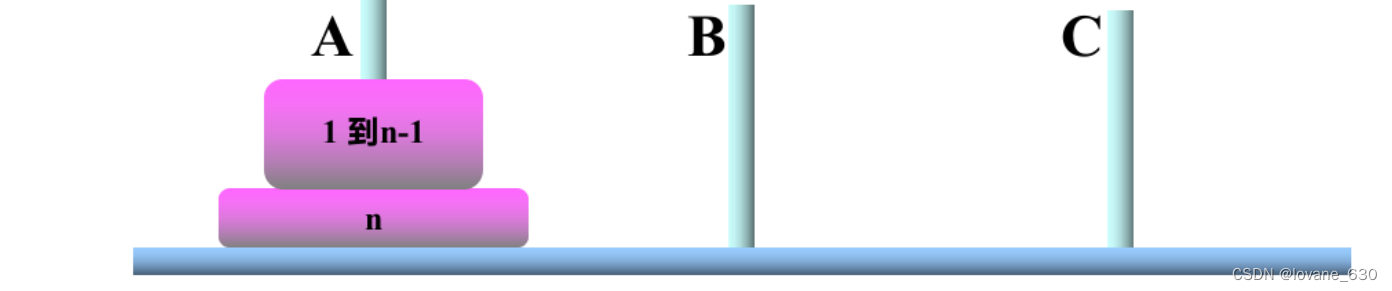

#n个盘子从A挪到C，借助B
def Move(n,A,B,C):#递归出口if n==0:return#n-1个盘子从A挪到BMove(n-1,A,C,B)#第n个盘子从A挪到Cprint("{}->{}".format(A,C))#n-1个盘子从B挪到CMove(n-1,B,A,C)n=int(input())
Move(n,'A','B','C')

---

#以上内容仅为本人知识归纳