聚类步骤

k-means通常被称为劳埃德算法，这在数据聚类中是最经典的，也是相对容易理解的模型。算法执行的过程分为4个阶段。

• 1.首先，随机设K个特征空间内的点作为初始的聚类中心。
• 2.然后，对于根据每个数据的特征向量，从K个聚类中心中寻找距离最近的一个，并且把该数据标记为这个聚类中心。
• 3.接着，在所有的数据都被标记过聚类中心之后，根据这些数据新分配的类簇，通过取分配给每个先前质心的所有样本的平均值来创建新的质心重,新对K个聚类中心做计算。
• 4.最后，计算旧和新质心之间的差异,如果所有的数据点从属的聚类中心与上一次的分配的类簇没有变化，那么迭代就可以停止，否则回到步骤2继续循环。K均值等于具有小的全对称协方差矩阵的期望最大化算法

k-means API

from sklearn.cluster import KMeans
参数:
sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
k-means聚类
n_clusters:开始的聚类中心数量
init:初始化方法，默认为’k-means ++’

labels_:默认标记的类型，可以和真实值比较（不是值比较）

class sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')""":param n_clusters:要形成的聚类数以及生成的质心数:param init:初始化方法，默认为'k-means ++',以智能方式选择k-均值聚类的初始聚类中心，以加速收敛;random,从初始质心数据中随机选择k个观察值（行:param n_init：int，默认值：10使用不同质心种子运行k-means算法的时间。最终结果将是n_init连续运行在惯性方面的最佳输出。:param n_jobs：int用于计算的作业数量。这可以通过并行计算每个运行的n_init。如果-1使用所有CPU。如果给出1，则不使用任何并行计算代码，这对调试很有用。对于-1以下的n_jobs，使用（n_cpus + 1 + n_jobs）。因此，对于n_jobs = -2，所有CPU都使用一个。:param random_state:随机数种子，默认为全局numpy随机数生成器"""

聚类建立模型

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import numpy as np# 使用的数据
X = np.array([[1, 2], [1, 4], [1, 0],[4, 2], [4, 4], [4, 0]])kmeans = KMeans(n_clusters=2, random_state=0) # 导入模型,分为两个模块(n_clusters=2)
kmeans.fit(X) # 进行训练分类print('每个点的类别',kmeans.cluster_centers_)
print('集群中心的点坐标:',kmeans.labels_)
print('将这些值进行分类:',kmeans.predict(X))
print('预测这个两个数属于那个类型:',kmeans.predict([[0, 0], [4, 4]]))
print('Kmeans性能评估(计算所有样本的平均轮廓系数):',silhouette_score(X,kmeans.predict(X)))

• 特点分析：

  • 采用迭代式算法，直观易懂并且非常实用

  • 缺点：容易收敛到局部最优解(多次聚类)
    需要预先设定簇的数量(k-means++解决)

Kmeans性能评估指标

注：对于每个点i 为已聚类数据中的样本 ，b_i 为i 到其它族群的所有样本的平均
距离，a_i 为i 到本身簇的距离平均值

最终计算出所有的样本点的轮廓系数平均值

这个举一个二维数据的例子:
假设这个是一个分类好的一个聚类,我们以蓝1为例:

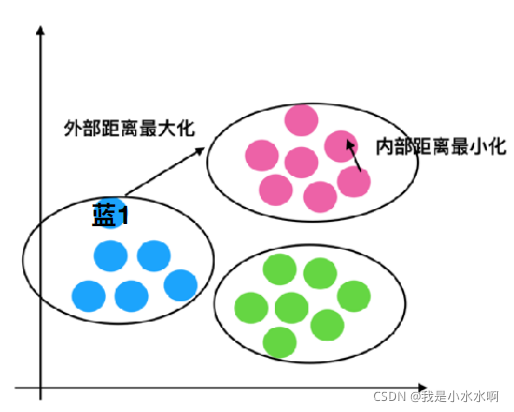
1、计算蓝1到⾃身类别的点距离的平均值a_i
2、计算蓝1分别到红⾊类别，绿⾊类别所有的点的距离，求出平均值b1, b2，取其中最⼩的值当做b_i

• 我们以轮廓系数公式算出两个极端:
  b_i>>a_i : 1 是最好的(轮廓系数为1是完美的)
  a_i>> b_i :-1 是最差的(轮廓系数为-1是最差的)

• 可得 :轮廓系数范围 [-1, 1]

• 结论:

  • 如果sc_i 小于0，说明a_i 的平均距离大于最近的其他簇。
    聚-类效果不好

  • 如果sc_i 越大，说明a_i 的平均距离小于最近的其他簇。
    聚类效果好

  • 轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优

Kmeans性能评估指标API

sklearn.metrics.silhouette_score
sklearn.metrics.silhouette_score(X, labels)
计算所有样本的平均轮廓系数
X：特征值
labels：被聚类标记的目标值

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import numpy as np# 使用的数据
X = np.array([[1, 2], [1, 4], [1, 0],[4, 2], [4, 4], [4, 0]])kmeans = KMeans(n_clusters=2, random_state=0) # 导入模型,分为两个模块(n_clusters=2)
kmeans.fit(X) # 进行训练分类print('每个点的类别',kmeans.cluster_centers_)
print('集群中心的点坐标:',kmeans.labels_)
print('预测这个两个数属于那个类型:',kmeans.predict(X))print('Kmeans性能评估(计算所有样本的平均轮廓系数):',silhouette_score(X,kmeans.predict(X)))