Leetcode 3.18

Leetcode hot100

二叉树
- 1.路径总和 III
- 2.路径总和 II
- 3.二叉树的所有路径
- 4.二叉树的最近公共祖先
回溯
- 1.电话号码的字母组合

二叉树

1.路径总和 III

路径总和 III
思路：我们访问每一个节点 node，检测以 node 为起始节点且向下延深的路径有多少种。递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。
综上：递归是比较合适的方法。

当前层需要干什么：求出以当前 root 为节点向下遍历的和 == targetsum 的个数
rootSum(TreeNode* root, int targetSum)
以当前节点 p 为目标路径的起点递归向下进行搜索。假设当前的节点 p 的值为 val，我们对左子树和右子树进行递归搜索，对节点 p 的左孩子节点 pl 求出 rootSum(pl, targetSum−val)
以及对右孩子节点 pr 求出 rootSum(pr, targetSum−val)。节点 p 的 rootSum(p, targetSum)即等于 rootSum(pl,targetSum−val) + rootSum(pr,targetSum−val)，同时我们还需要判断一下当前节点 p 的值是否刚好等于 targetSum。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://以各个节点为根节点//root,root->left,root->right，root->left->left,root->left->right......int pathSum(TreeNode* root, int targetSum) {if (root == nullptr) return 0;return rootSum(root, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);}//以当前节点为根节点，找到从当前节点向下遍历，节点相加和为target的次数int rootSum(TreeNode* root, long targetSum) {if (root == nullptr) return 0;int ret = 0;if (root->val == targetSum) ret++;ret += rootSum(root->left, targetSum - root->val);ret += rootSum(root->right, targetSum - root->val);return ret;}
};

2.路径总和 II

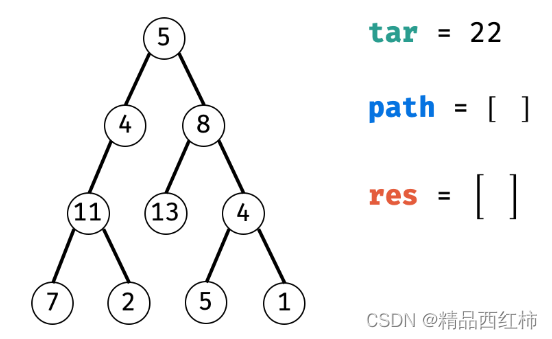
路径总和 II
虽然这道题不在hot100里，但是和上一道题很类似，该题是求所有 从根节点到叶子节点 路径总和等于给定目标和的路径。显然还是用递归的方法更合适。
我们可以递归遍历记录所有的路径，同时计算路径和，如果等于那么添加到最终的vector<vector< int >>中。

函数 dfs(TreeNode* root, int targetSum) ：

递推参数：当前节点 root ，当前目标值 targetSum。
终止条件：若节点 root 为空，则直接返回。
递推工作：
路径更新：将当前节点值 root->val 加入路径 vector<int>tmp 。
目标值更新： targetSum = targetSum - root->val （即目标值 targetSum 从 targetSum 减至 0 ）。
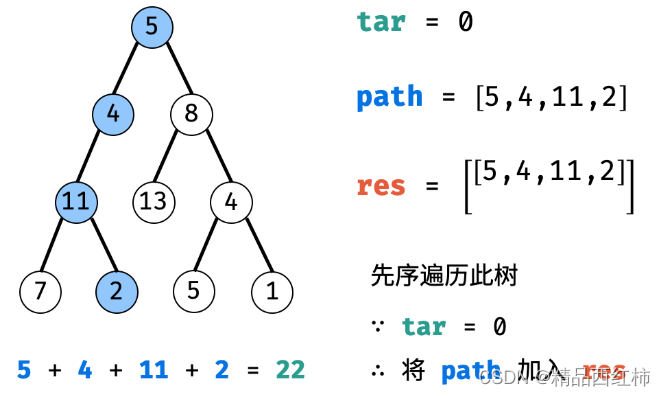
路径记录：当 (1) root 为叶节点(左右子树均为空) 且 (2) 路径和等于目标值(targetSum == 0)，则将此路径 tmp 加入 ans 。
先序遍历：递归左 / 右子节点。
路径恢复：向上回溯前，需要将当前节点从路径 tmp 中删除，即执行 tmp.pop_back() 。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> ans;vector<int> tmp;vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if (root == nullptr) return ans;dfs(root, targetSum);return ans;}void dfs(TreeNode* root, int targetSum) {if (root == nullptr) return;tmp.push_back(root->val);targetSum -= root->val;if (root->left == nullptr && root->right == nullptr && targetSum == 0) {ans.push_back(tmp);}dfs(root->left, targetSum);dfs(root->right, targetSum);tmp.pop_back();}
};

在这里插入图片描述

3.二叉树的所有路径

二叉树的所有路径
再来看一道相似的题目，只需要记录从根节点到叶子节点的路径即可

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> ans;vector<string> binaryTreePaths(TreeNode* root) {if (root == nullptr) return ans;string tmp;dfs(root, tmp);return ans;}void dfs(TreeNode* root, string tmp) {if (root == nullptr) return;tmp += to_string(root->val);if (root->left == nullptr && root->right == nullptr) {ans.push_back(tmp);} else {tmp += "->";dfs(root->left, tmp);dfs(root->right, tmp);}}
};

4.二叉树的最近公共祖先

二叉树的最近公共祖先
终止条件：

当 root 等于 p,q，则直接返回 root；

递推工作：

开启递归左子节点，返回值记为 left；
开启递归右子节点，返回值记为 right；

返回值：
根据 left 和 right，可展开为四种情况；

当 left 和 right 同时为空：说明 root 的左 / 右子树中都不包含 p,q，返回 null；
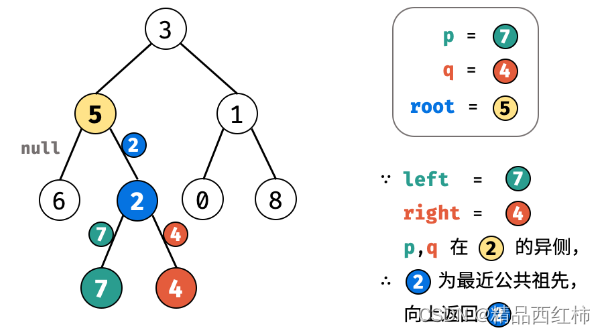
当 left 和 right 同时不为空：说明 p,q 分列在 root 的异侧（分别在左 / 右子树），因此 root
为最近公共祖先，返回 root ；
当 left 为空，right 不为空：p,q 都不在 root 的左子树中，直接返回 right。
具体可分为两种情况：
- p,q 其中 p 在 root 的右子树中，此时 right 指向 p（假设为 p ）；
- p,q 两节点都在 root 的右子树中，此时的 right 指向最近公共祖先节点；
当 left 不为空， right 为空：与情况 3. 同理；
参考

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//找到p，找到q，或者已经到叶子节点还没找到if (root == nullptr || root == p || root == q) return root;//遍历左子树TreeNode* left = lowestCommonAncestor(root->left, p, q);//遍历右子树TreeNode* right = lowestCommonAncestor(root->right, p, q);//左右子树点都没找到if (left == nullptr && right == nullptr) return nullptr;//右边没有p或者q，left要么是p/q，或者是p/q的公共祖先if (left != nullptr && right == nullptr) return left;if (right != nullptr && left == nullptr) return right;return root;}
};

回溯

1.电话号码的字母组合

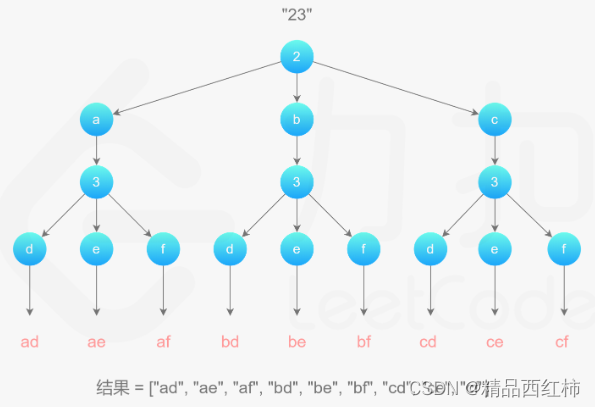
电话号码的字母组合
电话号码的组合就是输入字符对应字符串的全排列，全排列的问题应该用回溯解决。
遍历输入的字符串;
找出对应字符映射的字母;
遍历映射字母;
添加到tmp string中，进行递归;
tmp string 剪枝。
在这里插入图片描述

class Solution {
public:unordered_map<char, string> mp = {{'2', {"abc"}},{'3', {"def"}},{'4', {"ghi"}},{'5', {"jkl"}},{'6', {"mno"}},{'7', {"pqrs"}},{'8', {"tuv"}},{'9', {"wxyz"}}};vector<string> ans;vector<string> letterCombinations(string digits) {if (digits.empty()) return ans;string tmp;dfs(digits, 0, tmp);return ans;}void dfs(string digits, int index, string& tmp) {if (index == digits.length()) {ans.push_back(tmp);} else {//遍历输入的数字char digit = digits[index];//找到数字对应的stringstring letters = mp[digit];//遍历数字对应的charfor (char c: letters) {//添加到stringtmp.push_back(c);//递归dfs(digits, index + 1, tmp);tmp.pop_back();}}   }
};