Exercise 12.1-1
任何时候,如果一个节点有一个子节点,就把它当作右子节点,左子节点为NIL。
Exercise 12.1-2
二叉搜索树的属性保证了左子树的所有节点都更小,右子树的所有节点都更大。最小堆属性只保证一般的子节点大于父节点的关系,但不区分左右子节点。因此,min-heap 属性不能用于在线性时间内按排序顺序打印出键,因为我们没有办法知道哪个子树包含下一个最小的元素。
Exercise 12.1-3
我们对习题 10.4-5 的解决方案解决了这个问题。
Exercise 12.1-4![]()
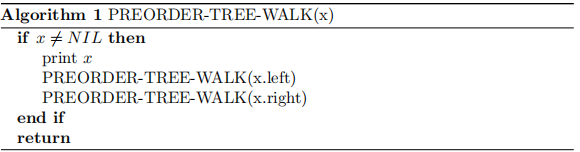
我们调用 T.root 上的每个算法。参见算法 PREORDER-TREE- WALK 和 POSTORDER-TREE-WALK。
Exercise 12.1-5
假设有一个矛盾我们可以在最坏情况下建立一个 BST 时间为 o(nlgn),然后, 为了排序,我们只需要构造 BST 然后读取无序遍历中的元素。第二步可以通过定理 12.1 在时间 Θ(n)内完成。同样,无序遍历必须是有序的,因为左子树中的元素都是比当前元素小的元素,它们都在当前元素之前被打印出来,而右子树的元素都是比当前元素大的元素,它们在当前元素之后被打印出来。这样就可以让我们在 o(n lg(n))时间内对一个矛盾进行排序。

Exercise 12.2-1

选项 c 不可能是探索的节点序列,因为我们从 911 节点取了左子节点,但 不知何故设法到达了 912 节点,该节点不属于 911 的左子树,因为它更大。选 项 e 也是不可能的,因为我们在 347 节点上取右子树,但后来遇到了 299 节点。
Exercise 12.2-2![]()
参见TREE-MINIMUM和TREE-MAXIMUM。
Exercise 12.2-3
![]()
Exercise 12.2-4
假设我们在这棵树中搜索4。 则 A = {2}, B = {1, 3, 4}, C =∅ ,班扬教授的主张因 1 < 2 而失败。
Exercise 12.2-5
假设节点x有两个子节点。然后它的后继是 BST 在 x右的最小元素。如果它有一个左子元素,那么它就不是最小元素。所以,它一定没有左子元素。同样,前导必须是左子树的最大元素,所以不能有右子树。
Exercise 12.2-6
首先我们确定 y 一定是 x的祖先,如果 y 不是 x的祖先,则设 z 表示 x和 y的第一个共同祖先,根据二叉搜索树的性质,x < z < y,因此 y 不能是 x的后继。
接下来观察 y.left 必须是 x 的祖先,因为如果它不是,那么 y.right 将是 x的祖先,这意味着 x > y.最后,假设 y 不是 x的最低祖先,它的左子也是 x的祖先,设 z 表示这个最低祖先。那么 z 一定在 y 的左子树中,这意味着 z < y,这与 y 是 x的后继结点的事实相矛盾。
Exercise 12.2-7
为了在运行时上显示这个边界,我们将展示使用这个过程,我们遍历每条边两次。这就足够了,因为树中边的数量比顶点的数量少一个。考虑一个 BST 的顶点,比如 x。然后,我们知道,当在 x.p 上调用后继函数时,在 xp 和 x之间的边被使用,当在以 x为根的子树的最大元素上调用它时,它又被使用。因为除了最初找到树的最小值外,这是唯一两次可以使用这条边。我们知道运行时间是 O(n)。我们得到的运行时间是 Ω(n)因为这是输出的大小。
Exercise 12.2-8
设 x是我们调用 TREE-SUCCESSOR 的节点,y 是 th x的 k - successor。设 z是 x 和 y 的最低共同祖先。连续调用永远不会遍历一条边超过两次,因为TREE-SUCCESSOR 的行为类似于树遍历,所以我们永远不会检查单个顶点超过三次。此外,任何键值不在 x 和 y 之间的顶点将最多检查一次,并且它将发生在从 x到 z 或 y 到 z 的简单路径上。由于这些路径的长度以 h 为界,因此运行时间可以以 3k + 2h = O(k + h)为界。
Exercise 12.2-9
如果 x = y.left,则在 x上调用继任者将不会导致 while 循环的迭代,因此将返回 y。类似地,如果 x = y.right,调用前身(参见练习 3)的 while 循环将不会运行多次,因此将返回 y。然后,只需要认识到问题要求显示的是 y 是前身(x)还是后继(x)。
Exercise 12.3-1
对TREE-INSERT-REC的初始调用应该是NIL, T.root , z
Exercise 12.3-2![]()
![]()
在 TREE-INSERT 的 while 循环中检查的节点与在 TREE-SEARCH 中检查的节点相同。在 TREE-INSERT 的第 9 到 13 行中,只检查了一个额外的节点。
Exercise 12.3-3
最坏的情况是,所形成的树的高度为 n,因为我们按照已经排序好的顺序插入它们。这将导致运行时间为 Θ(n2)。在最好的情况下,形成的树是近似平衡的。这将意味着高度不超过 O(lg(n))。注意它不能有更小的高度,因为高度为 h的完全二叉树只有 Θ(2 h )个元素。这将导致运行时间为 O(n lg(n))。我们在练习12.1-5 中展示了 Ω(n lg(n))。
Exercise 12.3-4
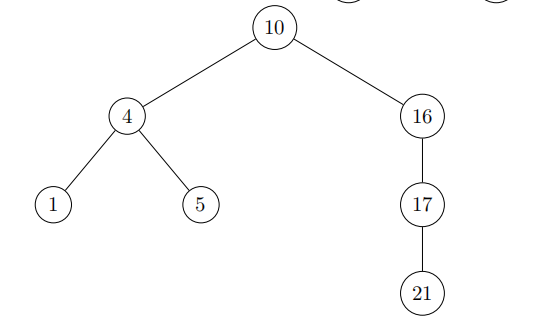
删除是不可交换的。在下面的树中,删除 1 然后删除 2 得到的结果与删除2 然后删除 1 得到的结果不同。
Exercise 12.3-5
我们的插入过程与 12.3-1 的解决方案密切相关,不同之处在于,一旦它找到插入给定节点的位置,它就会适当地更新 suc 字段,而不是 z 的 p 字段。
我们的 Search 过程与前一节给出的版本没有变化对于删除过程,我们将假设所有键都是不同的,因为这是本章中经常出现的假设。然而,这将取决于它。我们的删除过程首先调用 search ,直到我们离要查找的节点只有一步之远,也就是说,它调用 TREE-PRED(T.root,z.key)
它可以使用这个 TREE-PRED 过程来计算 up和 vp。TRANSPLANT 程序。由于 TREE-DELETE 只调用 TRANSPLANT 的次数是恒定的,因此以这种方式将 TRANSPLANT 的运行时间增加到 O(h)会导致新的TREE-DELETE 过程的运行时间为 O(h)。
Exercise 12.3-6
更新第 5 行,使 y 等于 TREE-MAXIMUM(z.left)。为了实现公平策略,我们可以在每次调用 TREE-DELETE 时随机决定是否使用前任或继任者。
Exercise 12.4-1
![]()
考虑大小为 4 的 n + 3 子集中最大元素的所有可能位置。假设它在某个i≤n− 1 的位置为 i + 4。然后,我们有 i+3 个位置,我们可以从中选择子集中剩下的三个元素。由于每个最大元素不同的子集都是不同的,我们只需将它们全部加起来就可以得到总数(包含排除原理)。
Exercise 12.4-2
为了保持平均深度较低但高度最大化,期望的树将是一个完整的二叉搜索树,但是长度为 c(n) 的链从其中一个叶节点垂下。设 k = log(n − c(n)) 为完整二叉搜索树的高度。则平均高度近似为 上界由最大的 c(n)给出,使得
上界由最大的 c(n)给出,使得
和 c(n) =ω(lg n) 一个可行的函数是
。
Exercise 12.4-3
假设我们有元素{1,2,3}。然后,如果我们用随机排序构造一棵树,那么,
我们得到的树出现的概率是 1/ 6 。然而,如果我们考虑键集 {1,2,3} 上所有有效的二叉搜索树。那么,我们将只有 5 种不同的可能性。所以,每一种发生的概率都是 1/5 ,这是一个不同的概率分布。
Exercise 12.4-4
![]()
二阶导数是
它总是正的,所以函数是凸的。
Exercise 12.4-5
假设快速排序总是选择中间的元素每次都是
个元素。然后,问题的大小每次至少以(1−k/2)次幂缩小。因此,最大递归深度d将使
,求解d,我们得到
。所以,
设A(n)表示在对长度为n的列表进行快速排序时,选择的某个枢轴不在中间
的概率。这不是以
的概率发生的。然后,我们得到两个子问题规模为n1, n2,且n1+n2=n-1,且
。因此,A(n)≤
。
因此,由于深度以O(1/ lg(n))为限,设是深度j处剩下的所有子问题的大小,因此,
。











)




)








![Vector[C++]](http://pic.xiahunao.cn/Vector[C++])



![[数据集][目标检测]铁路工人工服安全帽检测数据集3065张3类别](http://pic.xiahunao.cn/[数据集][目标检测]铁路工人工服安全帽检测数据集3065张3类别)