题目描述

达达帮翰翰给女生送礼物，翰翰一共准备了$N$ 个礼物，其中第$i$ 个礼物的重量是$G[i]$。

达达的力气很大，他一次可以搬动重量之和不超过$W$的任意多个物品。

达达希望一次搬掉尽量重的一些物品，请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。

输入格式

第一行两个整数，分别代表$W$ 和$N$。
以后$N$行，每行一个正整数表示$G[i]$。

输出格式

仅一个整数，表示达达在他的力气范围内一次性能搬动的最大重量。

数据范围

$1\le N\le 46$,
$1\le W,G[i]\le 2^{31}-1$

输入样例

20 5
7
5
4
18
1

输出样例

19

算法思想

根据题目描述，需要从给定的$N$个数中选择几个，使它们的和最接近$W$，属于“子集和”问题的扩展；当然也可以从背包问题的角度去思考解决，但是这里背包的“体积”过大（$1\le W\le 2^{31}-1$），时间和空间复杂度都不允许。

这类问题的直接解法就是进行“指数型”枚举，搜索每个礼物选还是不选，时间复杂度为$O(2^N)$。此题$N\le 46$，$2^{46}$的复杂度过高，可以利用双向深搜的思想进行优化。

双向深搜

除了迭代加深之外，双向深搜也可以避免在深层子树上浪费时间。

在一些题目中，问题不但具有“初态”，还具有明确的“终态”，并且从初态开始搜索与从终态开始逆向搜索产生的搜索树都能覆盖整个状态空间。在这种情况下，就可以采用双向搜索——从初态和状态出发各搜索一半，产生的两棵深度减半的搜索树，在中间交汇、组成最终答案。避免了层数过深时，分支数量的大规模增长。

下图是直接进行一次搜索产生的搜索树：

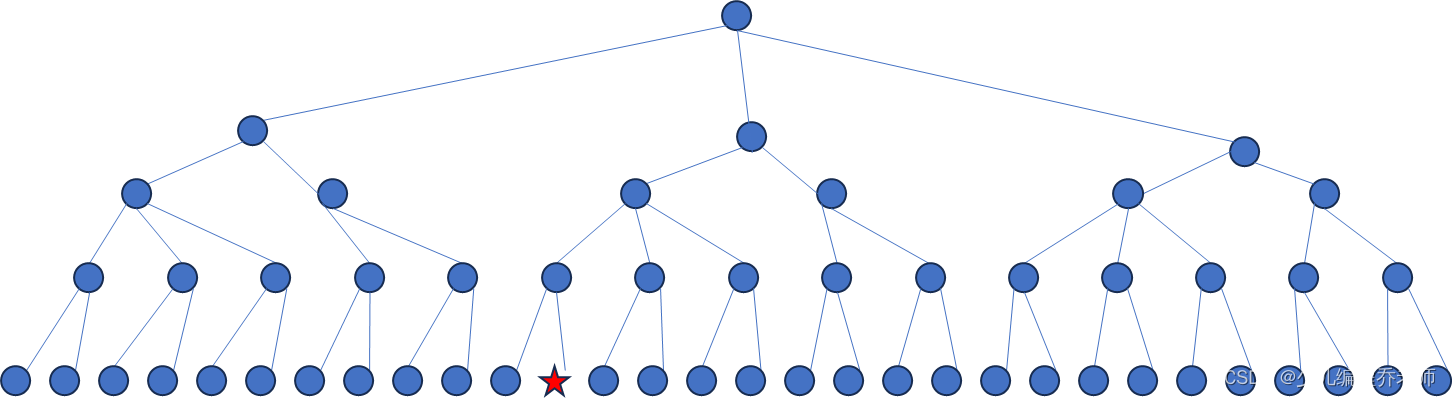
下图是双向搜索的两棵搜索树，避免了避免了层数过深时，分支数量的大规模增长。

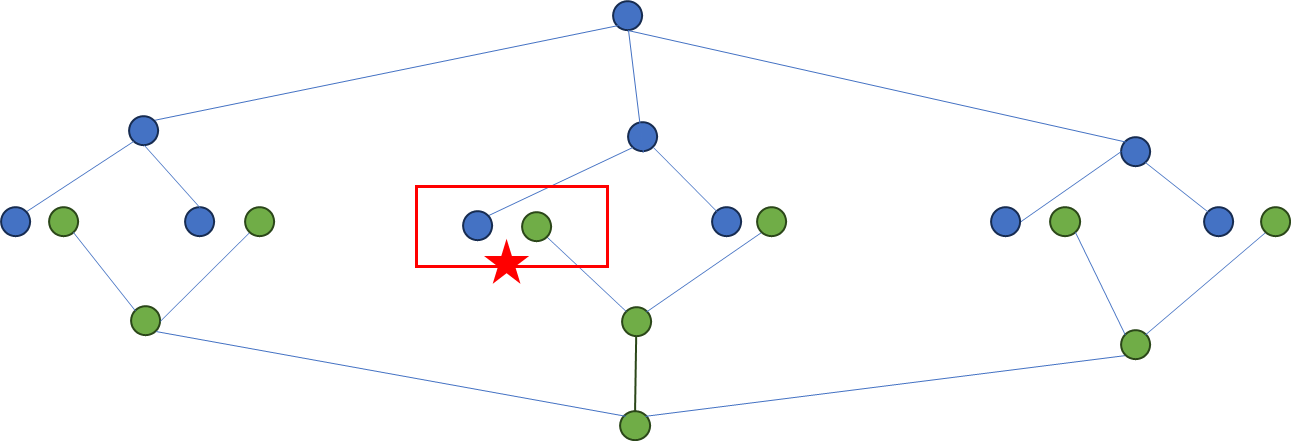
算法实现

将礼物分成两部分

• 首先，从前一半礼物中枚举出所有组合，将可能达到$0\sim W$之间的所有重量值，存放在一个数组$a[]$中，并对数组进行排序、去重
• 然后，进行第二次搜索，尝试从后一半礼物中枚举出所有组合，对于每个可能达到的重量$k$，在第一部分得到的数组$a[]$中查找$k+a[i]\le W$的最大值，可以使用二分查找。

这样，算法的时间复杂度为$O(2^{\frac{N}{2}}\times log\frac{N}{2})$。

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50;
int w[N];
int cnt, a[1 << 25]; //存储前一半礼物所有组合的重量
int n, W, ans;
void dfs1(int i, int k) //k表示目前组合的重量
{if(i == n / 2) //只搜索前一半的礼品{a[cnt ++] = k; //将组合得到的重量存到a数组return;}if((LL)k + w[i] <= W) dfs1(i + 1, k + w[i]); //装得下第i件礼物dfs1(i + 1, k); //不装第i件礼物
}
void dfs2(int i, int k)
{if(i == n) //搜索完成，二分查找不超过W的最大组合重量{int L = 0, R = cnt - 1;while(L < R){int mid = (L + R + 1) / 2;if((LL)k + a[mid] <= W) L = mid;else R = mid - 1;}ans = max(ans, k + a[L]);return;}if((LL)k + w[i] <= W) dfs2(i + 1, k + w[i]); //装得下第i件礼物dfs2(i + 1, k); //不装第i件礼物
}
int main()
{cin >> W >> n;for(int i = 0; i < n; i ++) cin >> w[i];//优化搜索顺序，优先搜索重量较大的礼品sort(w, w + n);reverse(w, w + n);dfs1(0, 0); //枚举前一半礼品的组合，将其组合得到的重量存到a数组sort(a, a + cnt); //对前一半礼物组合得到的重量排序去重cnt = unique(a, a + cnt) - a;//对后一半礼物进行搜索dfs2(n / 2, 0);cout << ans;return 0;
}