（三）OpenOFDM符号对齐

符号对齐

模块：sync_long.v
输入：I (16), Q (16), phase_offset (32), short_gi (1)
输出：long_preamble_detected (1), fft_re (16), fft_im (16)

检测到数据包后，下一步是精确确定每个 OFDM 符号的起始位置。在802.11中，每个OFDM符号是4微秒长的。在 20 MSPS 采样率下，这意味着每个 OFDM 符号包含 80 个样本。任务是将传入的样本流分组为 80 个样本的 OFDM 符号。这可以使用短前导码后面的长前导码来实现。

这部分是在实现数据包检测之后进行的，长前导码登场发挥作用。如果对这里的这些数字有疑惑，请先去搞清楚802.11 OFDM数据包的结构。下面我们将从长前导码的最起始位置（GI2）开始，将样本划分为80个样本一组的OFDM符号。

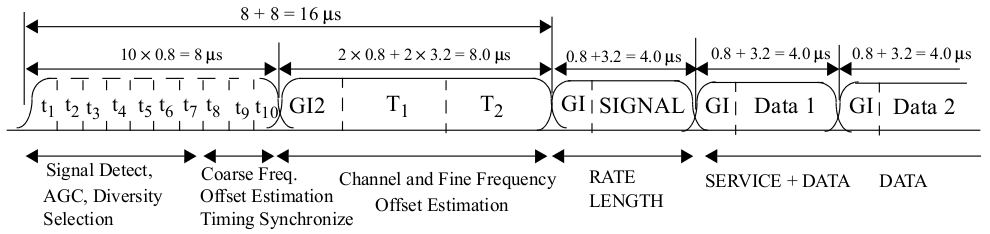
_images/training.png

图 9 802.11 OFDM 数据包结构（802.11-2012 Std 中的图 18-4）

如图9所示，长前导码持续时间为8微秒（160 个样本），包含两个相同的长训练序列（LTS），每个 64 个样本。LTS 是已知的，我们可以使用互相关来找到它。

样本i的交叉验证分数可以计算如下。

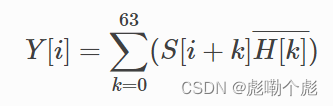
在这里H是时域中已知LTS的64个样本，并且可以在表L-6中找到（索引96至159）。可以找到 LTS（64 个样本）的 numpy 可读文件，可以这样读取：802.11-2012 stdhere

>>> import numpy as np
>>> lts = np.loadtxt('lts.txt').view(complex)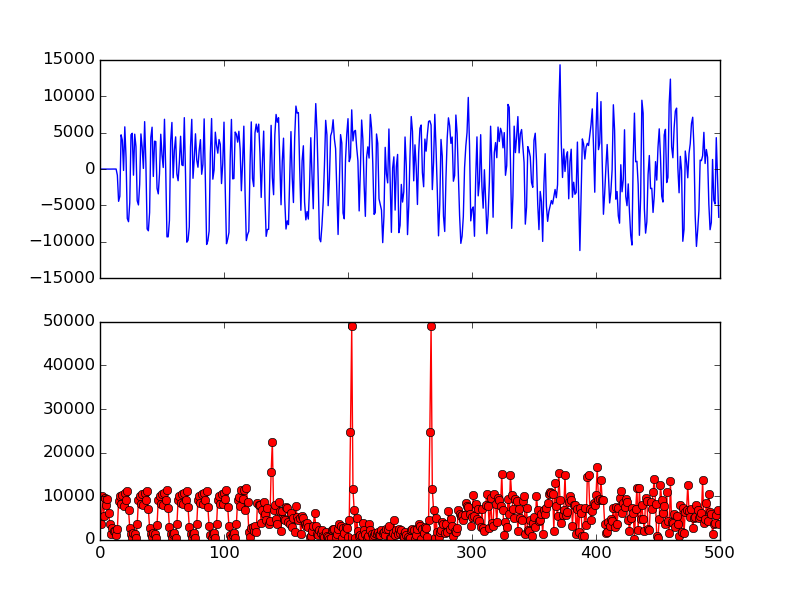

_images/lts.png

图 10长前导码和互相关结果

要绘制图 10，请加载数据文件（请参阅示例文件），然后：

# in scripts/decode.py
import decode
import numpy as np
from matplotlib import pyplot as pltfig, ax = plt.subplots(nrows=2, ncols=1, sharex=True)
ax[0].plot([c.real for c in samples][:500])
# lts is from the above code snippet
ax[1].plot([abs(c) for c in np.correlate(samples, lts, mode='valid')][:500], '-ro')
plt.show()

图 10显示了长前导码样本以及互相关的结果。我们可以清楚地看到两个尖峰对应于长前导码中的两个 LTS。尖峰宽度仅为 1 个样本，准确显示每个序列的开头。假设样本索引如果第一个尖峰是N，然后 160 个样本长前导码从样本开始N−32。

两个尖峰的位置就是802.11 OFDM数据包结构中T1，T2前面的虚线位置，这只是代表不包含保护间隔GI的长前导码起始位置，如果说加上了这两个GI，我们就还得在N（出现尖峰的位置）的基础上减去32，也就是减去16*2两个GI的长度，以确定最初始的位置。

这一切看起来都很美好，但当涉及到 Verilog 实现时，我们必须做出妥协。

从(1)我们可以看出，对于每个样本，我们需要执行64次复数乘法，这会消耗大量的FPGA资源。因此，我们需要减少交叉验证的规模。我们的想法是仅使用一部分而不是所有 LTS 样本。

下面主要就是说，因为资源有限，所以逐渐减少进行互相关的样本数量，看一下取到多少的时候出来的现象就已经能看到明显的尖峰，那就用这个样本数量去做互相关，既能节省资源又能达到想要的结果。

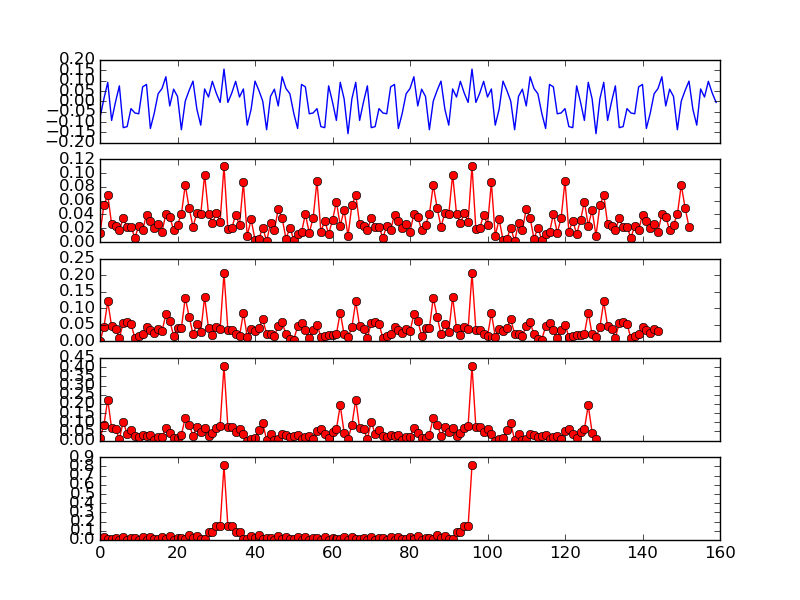
_images/match_size.png

图 11不同尺寸（8、16、32、64）的互相关

图 11可以绘制为：

lp = decode.LONG_PREAMBLEfig, ax = plt.subplots(nrows=5, ncols=1, sharex=True)
ax[0].plot([c.real for c in lp])
ax[1].plot([abs(c) for c in np.correlate(lp, lts[:8], mode='valid')], '-ro')
ax[2].plot([abs(c) for c in np.correlate(lp, lts[:16], mode='valid')], '-ro')
ax[3].plot([abs(c) for c in np.correlate(lp, lts[:32], mode='valid')], '-ro');
ax[4].plot([abs(c) for c in np.correlate(lp, lts, mode='valid')], '-ro')
plt.show()

图 11显示了长前导码（160 个样本）以及不同大小的交叉验证。可以看出，使用 LTS 的前 16 个样本足以表现出两个窄尖峰。因此，OpenOFDM 使用 LTS 的前 16 个样本的互相关来进行符号对齐。为了确认这一点，图 12显示了实际数据包上前 16 个 LTS 样本的互相关。这两个尖峰不像图10中的那样明显，但仍然清晰可见。

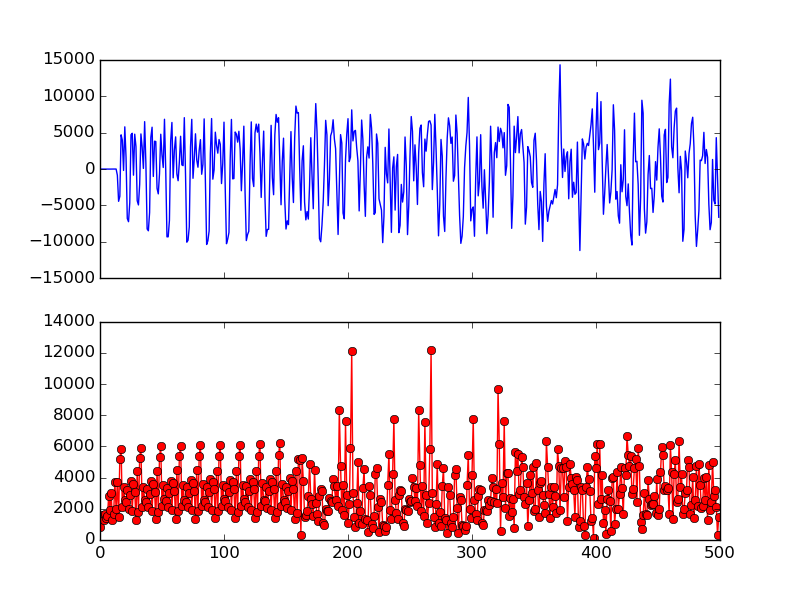
_images/lts_16.png

图 12使用 LTS 的前 16 个样本进行交叉验证

为了找到这两个峰值，我们记录了前 64 个样本的最大相关样本（因为第一个峰值应该位于第 32 个样本）。同样，我们还记录了第二个 64 个样本的最大相关样本。为了进一步消除误报，我们还检查两个尖峰样本索引是否为64±1。通过互相关确定了尖峰的位置还不够严谨，记录下两个尖峰的位置只有它们相差64±1的时候，才能正式确定，因为两个长前导码的开始正好相差64个样本长度。