目录

1、n-皇后问题（回溯模板）

2、木棒（《算法竞赛进阶指南》、UVA307）

3、飞机降落（第十四届蓝桥杯省赛C++ B组）

---

1、n-皇后问题（回溯模板）

n皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

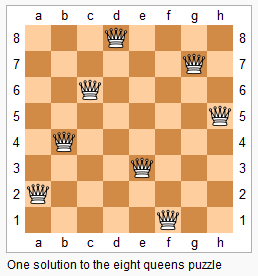
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..

思路：

经典的模板，这里的u代表行、col数组用来枚举标记列、dg用来枚举标记对角线、undg用来标记反对角线

代码：

#include<bits/stdc++.h>using namespace std;int n;const int N=10;char g[N][N];bool col[N],dg[N],undg[N];void dfs(int u)
{if(u==n)//找到一种方案 {for(int i=0;i<n;i++)puts(g[i]);puts("");return ;}for(int i=0;i<n;i++)//枚举列 {if(!col[i]&&!dg[u+i]&&!undg[u-i+n]){g[u][i]='Q';col[i]=dg[u+i]=undg[u-i+n]=true;dfs(u+1);col[i]=dg[u+i]=undg[u-i+n]=false;g[u][i]='.';}}
}
int main()
{cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)g[i][j]='.';dfs(0);return 0;	
} 

2、木棒（《算法竞赛进阶指南》、UVA307）

乔治拿来一组等长的木棒，将它们随机地砍断，使得每一节木棍的长度都不超过 50 个长度单位。

然后他又想把这些木棍恢复到为裁截前的状态，但忘记了初始时有多少木棒以及木棒的初始长度。

请你设计一个程序，帮助乔治计算木棒的可能最小长度。

每一节木棍的长度都用大于零的整数表示。

输入格式

输入包含多组数据，每组数据包括两行。

第一行是一个不超过 64 的整数，表示砍断之后共有多少节木棍。

第二行是截断以后，所得到的各节木棍的长度。

在最后一组数据之后，是一个零。

输出格式

为每组数据，分别输出原始木棒的可能最小长度，每组数据占一行。

数据范围

数据保证每一节木棍的长度均不大于 50。

输入样例：

9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0

输出样例：

6
5

思路：

关键剪枝条件：

1、如果上一次最终没有满足条件，回溯出来后如果我们还在拼第一根（cur==0），那么必定失败

2、如果上一次失败回溯出来后，我们正好满足现在的长度加上当前木棍长度==目标长度（cur+a[i]==len），那么必定失败

3、我们要跳过和当前长度相同的木棍，因为用这个长度必定失败

代码：

#include<bits/stdc++.h>using namespace std;const int N=70;int n;int len,sum;
int a[N];
bool st[N];//记录状态 
//cur表示当前的长度
//u表示拼接的个数 
//start表示从第几根开始拼 
bool dfs(int u,int cur,int start)
{if(u*len==sum)return true;//拼成所有的 if(cur==len)return dfs(u+1,0,0);for(int i=start;i<n;i++){if(st[i])continue;if(cur+a[i]<=len){st[i]=true;//表示第i根已经用过了 if(dfs(u,cur+a[i],i+1))return true;st[i]=false;}if(!cur || cur+a[i]==len)return false;//如果当前在拼新木棍或者是最后一根品好的木棍 int j=i+1;while(j<n && a[j]==a[i])j++;//跳过长度相同的木棍 i=j-1;}return false;
}int main()
{while(cin>>n,n!=0){len=sum=0;memset(st,false,sizeof st);for(int i=0;i<n;i++){cin>>a[i];	sum+=a[i];len=max(len,a[i]);} sort(a,a+n,greater<int>());while(true){if(sum%len==0 && dfs(0,0,0)){cout<<len<<endl;break;}len++;}}return 0;	
} 

3、飞机降落（第十四届蓝桥杯省赛C++ B组）

有 N 架飞机准备降落到某个只有一条跑道的机场。

其中第 i 架飞机在 Ti时刻到达机场上空，到达时它的剩余油料还可以继续盘旋 Di 个单位时间，即它最早可以于 Ti 时刻开始降落，最晚可以于 Ti+Di 时刻开始降落。

降落过程需要 Li个单位时间。

一架飞机降落完毕时，另一架飞机可以立即在同一时刻开始降落，但是不能在前一架飞机完成降落前开始降落。

请你判断 N 架飞机是否可以全部安全降落。

输入格式

输入包含多组数据。

第一行包含一个整数 T，代表测试数据的组数。

对于每组数据，第一行包含一个整数 N。

以下 N 行，每行包含三个整数：Ti，Di 和 Li。

输出格式

对于每组数据，输出 YES 或者 NO，代表是否可以全部安全降落。

数据范围

对于 30% 的数据，N≤2。
对于 100% 的数据，1≤T≤10，1≤N≤10，0≤Ti,Di,Li≤1e5。

输入样例：

2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20

输出样例：

YES
NO

样例解释

对于第一组数据，可以安排第 3 架飞机于 0 时刻开始降落，20 时刻完成降落。安排第 2 架飞机于 20时刻开始降落，30 时刻完成降落。安排第 1 架飞机于 30 时刻开始降落，40 时刻完成降落。

对于第二组数据，无论如何安排，都会有飞机不能及时降落。

思路：

关键：我们飞机最可以降落的最早时间是max(last,t)+l,因为就算飞机可以降落了，上一个飞机没有降落完成也是不行的，必须等到last结束才能降落，所以上上一辆飞机降落的时间取为max(last,t)+l

代码：

#include<bits/stdc++.h>using namespace std;const int N=20;struct plane
{int t,d,l;
}p[N]; int k,n;
int t[N],d[N],l[N];
bool st[N];//bool cmp(plane a,plane b)
//{
//	return a.t<b.t;
//}bool dfs(int cnt,int last)
{if(cnt>=n)//飞机达到数量 {return true;}for(int i=0;i<n;i++){int t=p[i].t;int d=p[i].d;int l=p[i].l;if(!st[i] && t+d>=last){st[i]=true;if(dfs(cnt+1,max(last,t)+l))return true;st[i]=false;}}return false;
}int main()
{cin>>k;while(k--){cin>>n;for(int i=0;i<n;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);p[i]={a,b,c};}memset(st,false,sizeof st);if(dfs(0,0))cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;	
}