Chapter 13 Techniques of Design-Oriented Analysis: The Feedback Theorem
从这一章开始讲负反馈Control系统和小信号建模.
13.2 The Feedback Theorem
首先介绍 Middlebrook’s Feedback Theorem
考虑下面负反馈系统
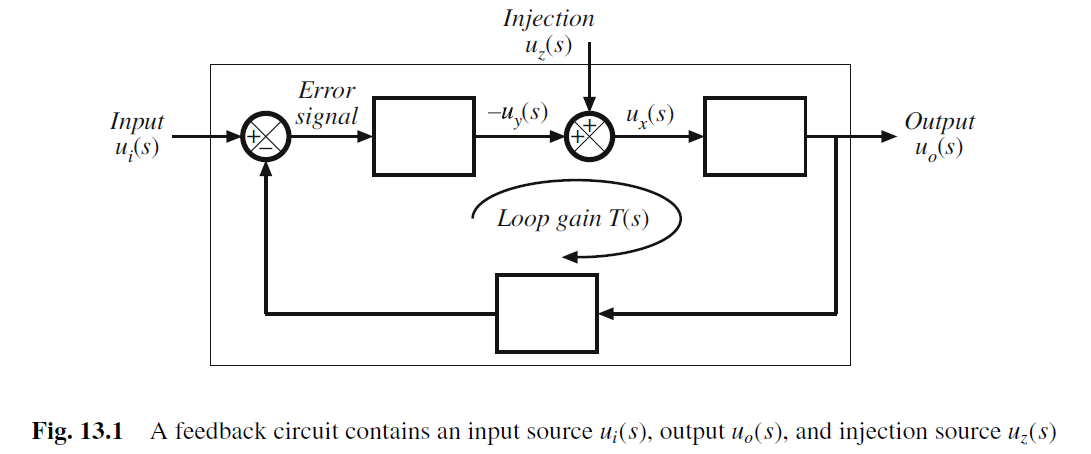
传输函数 G=uo/ui
G ( s ) = u o u i = G ∞ T 1 + T + G 0 1 1 + T G(s)=\frac{u_{o}}{u_{i}}=G_{\infty }\frac{T}{1+T}+G_{0}\frac{1}{1+T} G(s)=uiuo=G∞1+TT+G01+T1
T为Loop Gain 环路的增益
T ( s ) = u y ( s ) u x ( s ) ∣ u i = 0 T(s)=\frac{u_{y}(s)}{u_{x}(s)}\bigg|_{ui=0} T(s)=ux(s)uy(s) ui=0
ideal forward gain 理想正向增益, G_inf为通过uz 消除(null) uy后, ui到uo的传输函数.
G_inf其实就是利用运放虚短和虚断来推导Vout/Vin
G ∞ ( s ) = u o ( s ) u i ( s ) ∣ u y → 0 G_{\infty }(s)=\frac{u_{o}(s)}{u_{i}(s)}\bigg|_{u_y\to 0} G∞(s)=ui(s)uo(s) uy→0
当Loop Gain T-> inf时, G=G_inf
G0为通过uz 消除(null) ux后, ui到uo的传输函数
G 0 ( s ) = u o ( s ) u i ( s ) ∣ u x → 0 G_{0}(s)=\frac{u_{o}(s)}{u_{i}(s)}\bigg|_{u_x\to 0} G0(s)=ui(s)uo(s) ux→0
当Loop Gain T-> 0时, G=G0
Null loop Gain Tn(s): 引入Uz来消除null uo(s)
T n ( s ) = u y ( s ) u x ( s ) ∣ u 0 → 0 T_n(s)=\frac{u_{y}(s)}{u_{x}(s)}\bigg|_{u_0\to 0} Tn(s)=ux(s)uy(s) u0→0
T n ( s ) T ( s ) = G ∞ ( s ) G 0 ( s ) \frac{T_n (s)}{T(s)}=\frac{G_\infty (s)}{G_0(s)} T(s)Tn(s)=G0(s)G∞(s)
13.3 Example: Op Amp PD Compensator Circuit
我们以下面负反馈op-amp为例

假设运放为单极点系统
G o p ( s ) = G o p 0 ( 1 + s ω 1 ) G_{op}(s)=\frac{G_{op0}}{(1+\frac{s}{\omega_1})} Gop(s)=(1+ω1s)Gop0
Voltage injection模型为
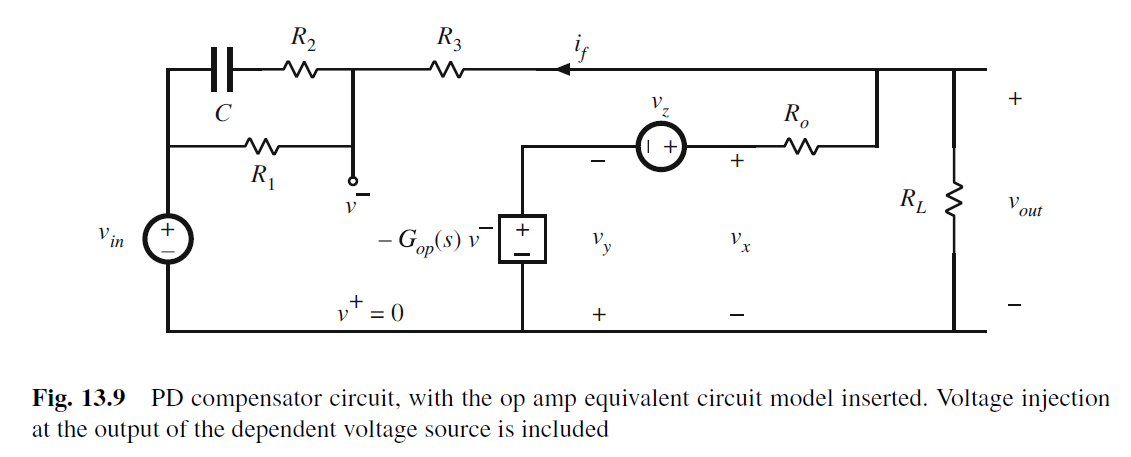
Ideal forward gain: 其实就是利用运放虚短和虚断来推导Vout/Vin, 即G_inf
G ∞ ( s ) = v o u t ( s ) v i n ( s ) ∣ v y → 0 G_{\infty }(s)=\frac{v_{out}(s)}{v_{in}(s)}\bigg|_{v_y\to 0} G∞(s)=vin(s)vout(s) vy→0
vy null to 0, 因此op输入端v-也被null to 0.
我们可以用运放的虚短和虚断特性来推导vout/vin. v- = v+ = 0即virtual ground

Loop Gain, T(s) 环路的增益.
T ( s ) = v o u t v x v − v o u t v y v − T(s)=\frac{v_{out}}{v_{x}}\frac{v{^-}}{v_{out}}\frac{v_y}{v{^-}} T(s)=vxvoutvoutv−v−vy
前两项就是电阻电容的voltage divider传输函数, 第三项为Gop
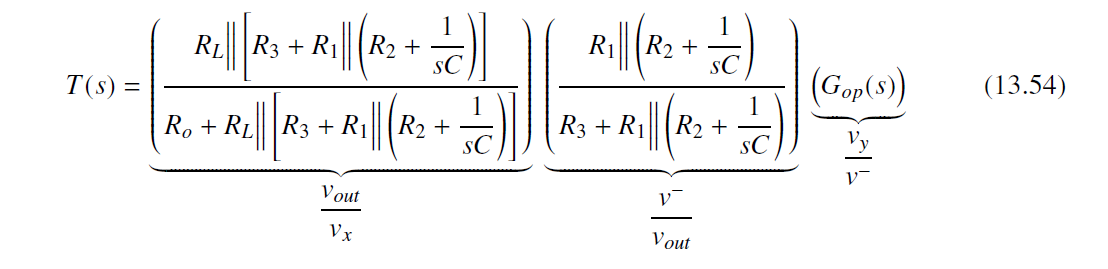
G0为调节Vz, 从而Vx nulled to 0. 即运放输出为0
G 0 ( s ) = v o u t ( s ) v i n ( s ) ∣ v x → 0 G_{0}(s)=\frac{v_{out}(s)}{v_{in}(s)}\bigg|_{v_x\to 0} G0(s)=vin(s)vout(s) vx→0
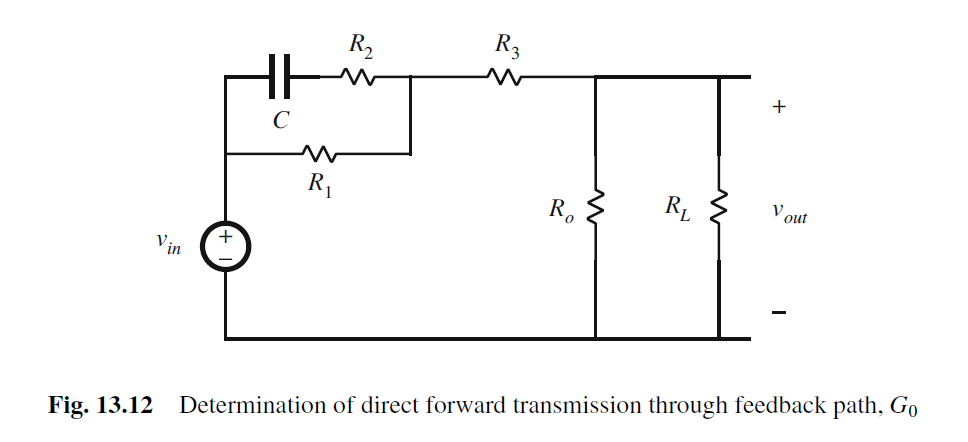
因此G0也是电阻电容的voltage divider传输函数

Tn为null output的loop gain
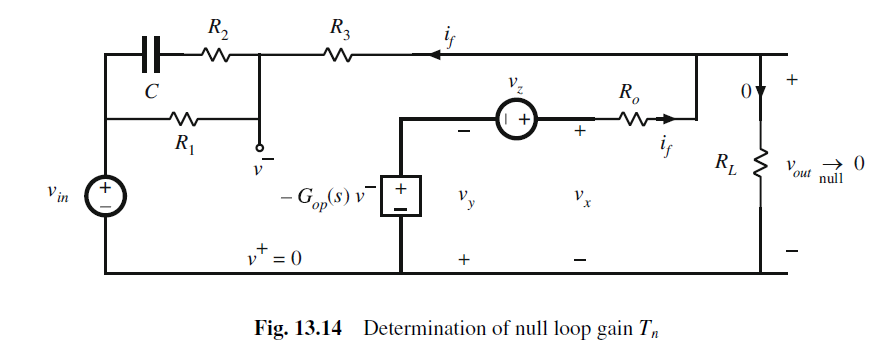
T n ( s ) = v y ( s ) v x ( s ) ∣ v o u t → 0 T_{n }(s)=\frac{v_{y}(s)}{v_{x}(s)}\bigg|_{v_{out}\to 0} Tn(s)=vx(s)vy(s) vout→0
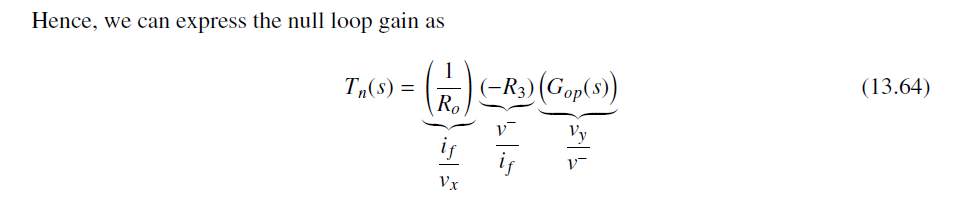
因此Loop Gain可推导为
T ( s ) = G 0 ( s ) T n ( s ) G ∞ ( s ) T(s)=\frac{G_{0}(s)T_{n}(s)}{G_{\infty }(s)} T(s)=G∞(s)G0(s)Tn(s)
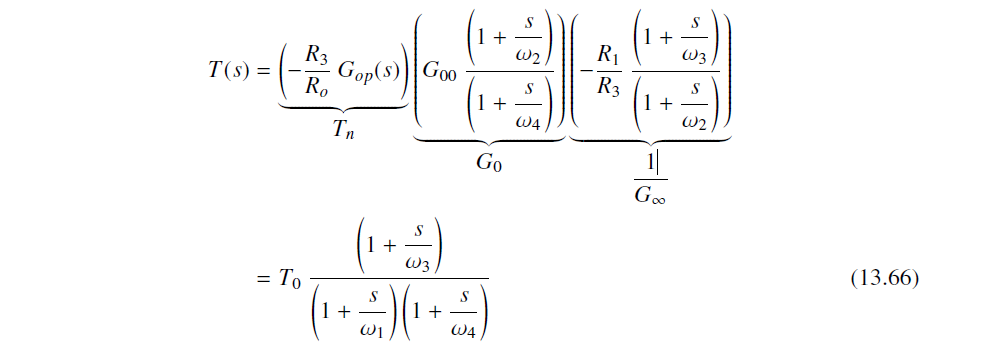
最终Transfer Function, G= Vout/Vin
G ( s ) = v o u t v i n = G ∞ T 1 + T + G 0 1 1 + T G(s)=\frac{v_{out}}{v_{in}}=G_{\infty }\frac{T}{1+T}+G_{0}\frac{1}{1+T} G(s)=vinvout=G∞1+TT+G01+T1

f<30MHz, G0/(1+T)很小,
当f<fc (crossover frequency),G = G_inf
当f>fc (crossover frequency), G和G_inf差异很大
13.4 Example: Closed-Loop Regulator
Chapter 14 Circuit Averaging, Averaged Switch Modeling, and Simulation
这一章讲电路的平均化 Circuit averaging.
其核心思想就是把switch+diode替换成理想开关, 然后加上小信号模型
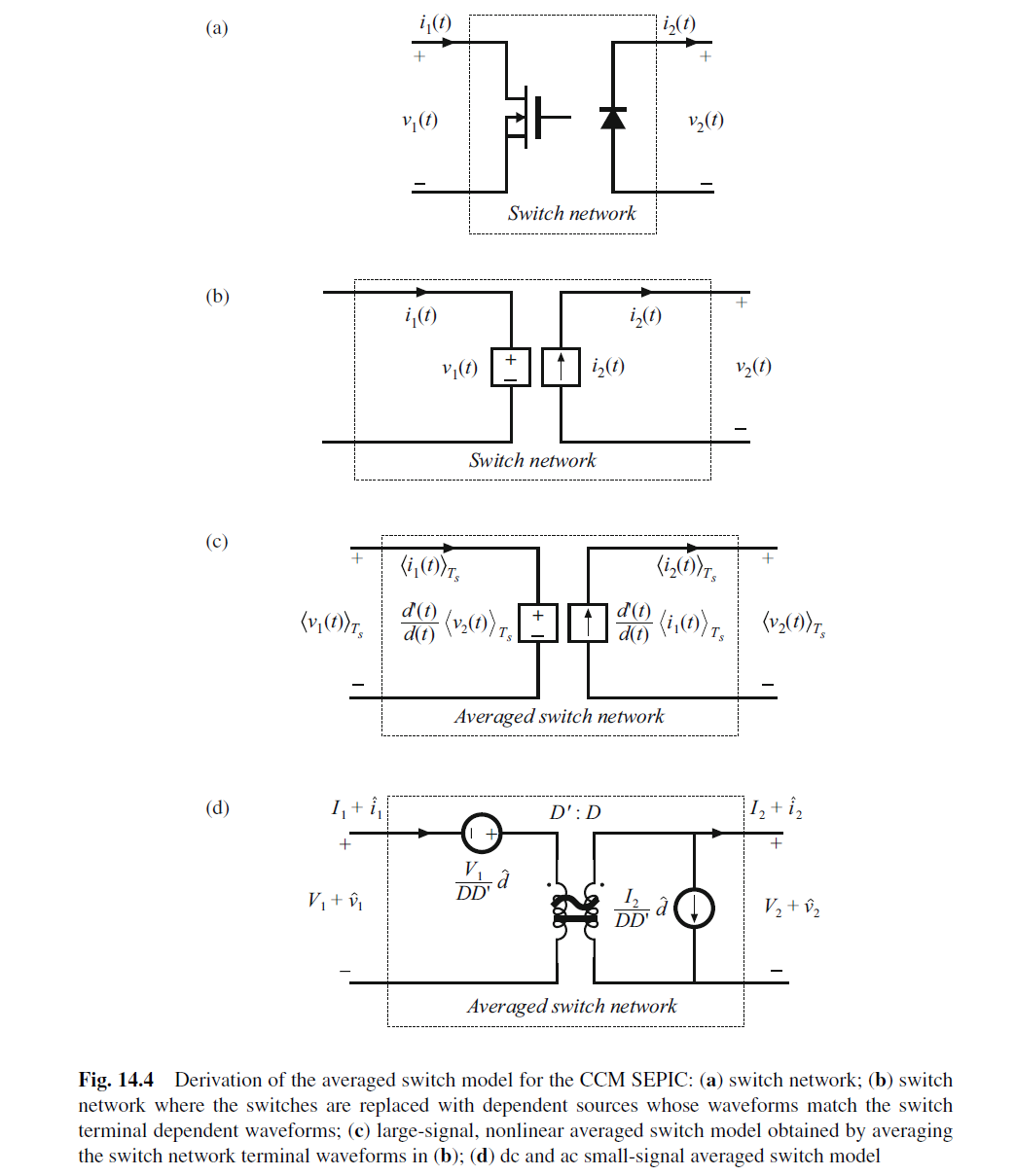
buck, boost, general two-switch的小信号模型如下
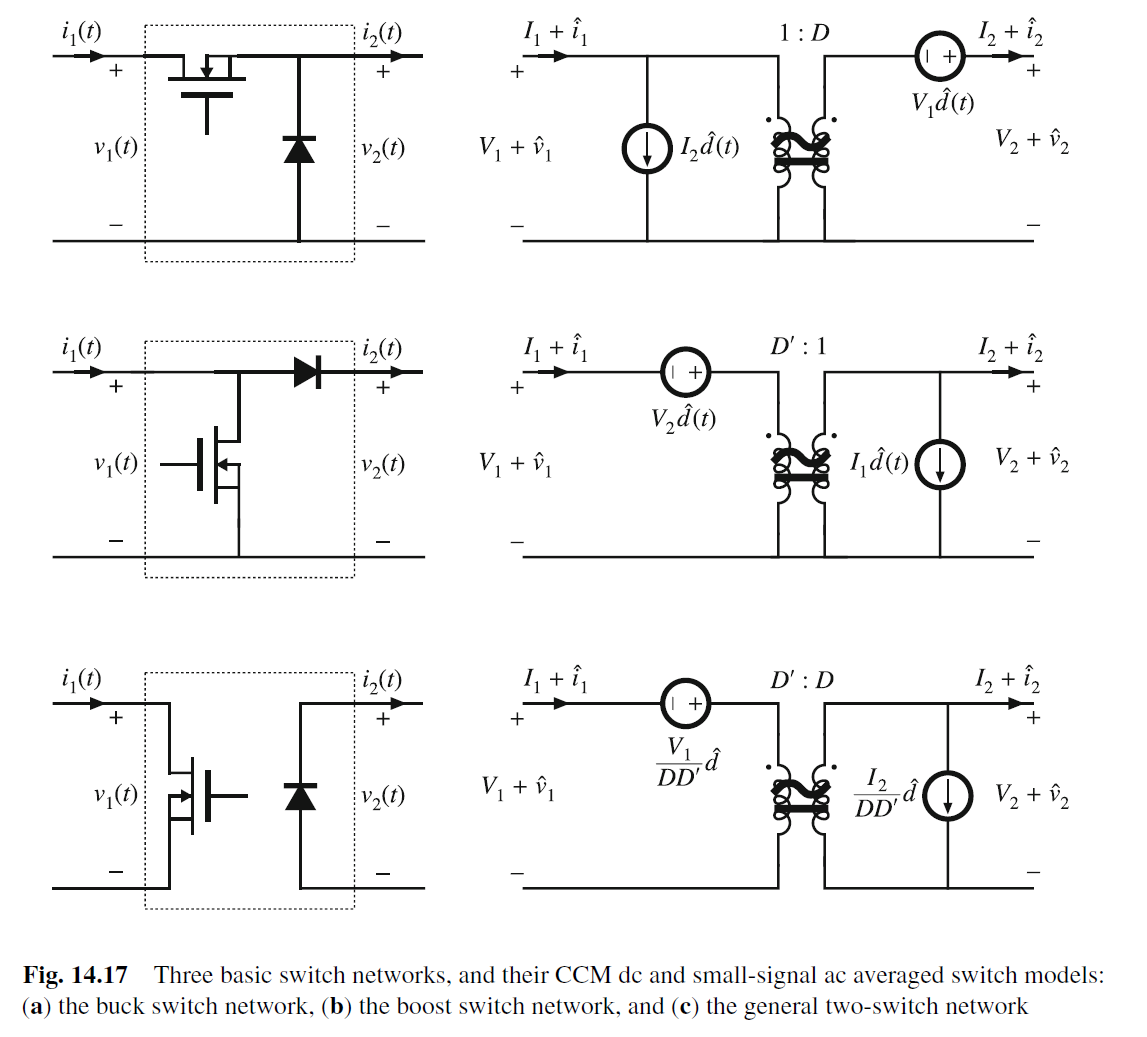
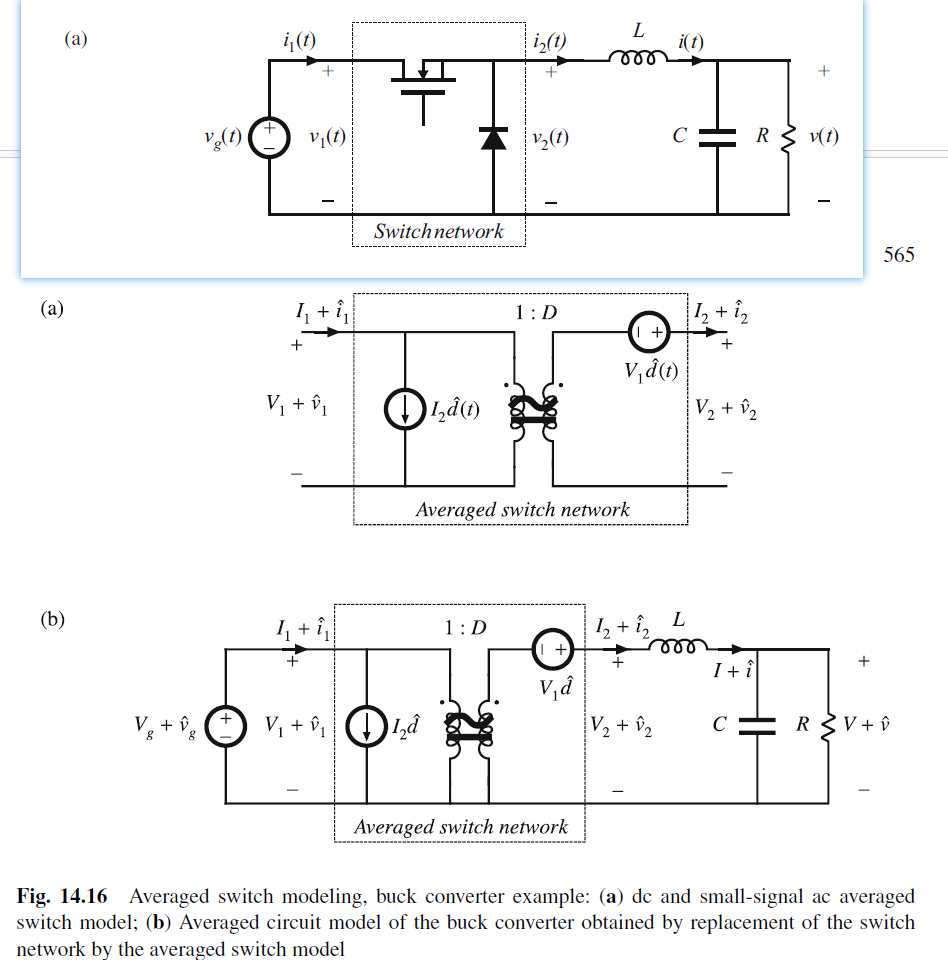
这样就能推导出converter的小信号模型了
对于电力电子系统的设计和仿真, 分为三种:
- 利用自带的器件库, 采用Cadence, SPICE, LTSpice等工具进行transient仿真. 好处精度高, 坏处费时费力.
- 简化器件模型, MOS换成Ron, 用PLECS and SIMPLIS仿真
- 平均化模型. 研究steady-state下电压,电流波形, 忽略ripple. 研究小信号模型. 可以给设计insight提供指导.



并配置vs)










分别使用js和jQuery代码实现)
)



